大闸蟹的 O O 第三单元日子——中测与强测的惨烈修罗场
第三单元是大闸蟹体验及其差的一单元,鬼知道从一开始的自信慢慢到最后的自暴自弃我都经历了什么,我已经感觉到分数与gpa与头发都在渐渐和我说再见了
JML基础梳理及工具链
JML(Java Modeling Language)是用于对Java程序进行规格化设计的一种表示语言。其旨在无需了解方法等的内部实现,而告诉读者方法等需要的前提条件以及运行后的结果等,这对于构建测试、维护代码、以及协作编程都都有极其重要的作用。
JML以javadoc注释的方式来表示规格,每行都以@起头。有两种注释方式,行注释和块注释。其中行注释的表示方式 为 //@annotation ,块注释的方式为 /* @ annotation @*/ 。一边规格都在描述对象的上部。
JML的语法主要有以下几个部分组成。
原子表达式:
\result表达式:表示一个非 void 类型的方法执行所获得的结果,即方法执行后的返回值,return的值。
\old( expr )表达式:用来表示一个表达式 expr 在相应方法执行前的取值,由于方法可能会对某些量进行更改,这是使用原值就可以用\old()表达式。
\not_assigned(x,y,...)表达式:用来表示括号中的变量是否在方法执行过程中被赋值。如果没有被赋值,返回为 true ,否则返回 false 。
\not_modified(x,y,...)表达式:该表达式限制括号中的变量在方法执行期间的取 值未发生变化。
\nonnullelements( container )表达式:表示 container 对象中存储的对象不会有 null 。
\type(type)表达式:返回类型type对应的类型(Class)。
\typeof(expr)表达式:该表达式返回expr对应的准确类型。
其中,最常用的为result和old表达式。
量化表达式:
\forall表达式:全称量词修饰的表达式,表示对于给定范围内的元素,每个元素都满足相应的约束。
\exists表达式:存在量词修饰的表达式,表示对于给定范围内的元素,存在某个元素满足相应的约束。
\sum表达式:返回给定范围内的表达式的和。
\product表达式:返回给定范围内的表达式的连乘结果。
\max表达式:返回给定范围内的表达式的最大值。
\min表达式:返回给定范围内的表达式的最小值。
\num_of表达式:返回指定变量中满足相应条件的取值个数。
其中forall和exists比较常用,尤其是包含数组或者MAP的结构中。
集合表达式:
集合构造表达式:可以在JML规格中构造一个局部的集合(容器),明确集合中可以包含的元素。(不太常用)
操作符:
子类型关系操作符: E1<:E2 ,如果类型E1是类型E2的子类型(sub type),则该表达式的结果为真,否则为假。
等价关系操作符: b_expr1<==>b_expr2 或者 b_expr1<=!=>b_expr2 ,其中b_expr1和b_expr2都是布尔表达 式,这两个表达式的意思是 b_expr1==b_expr2 或者 b_expr1!=b_expr2 。
推理操作符: b_expr1==>b_expr2 或者 b_expr2<==b_expr1 。对于表达式 b_expr1==>b_expr2 而言,当 b_expr1==false ,或者 b_expr1==true 且 b_expr2==true 时,整个表达式的值为 true 。
变量引用操作符:除了可以直接引用Java代码或者JML规格中定义的变量外,JML还提供了几个概括性的关键词来 引用相关的变量。\nothing指示一个空集;\everything指示一个全集,即包括当前作用域下能够访问到的所有变量。
以上就是JML语言的主要组成部分。
JML语言最重要的作用是描述方法与描述类型,也就是方法规格与类型规格。
方法规格
方法规格的核心内容有三个方面,前置条件、后置条件和副作用约定。
前置条件(pre-condition) :前置条件通过requires子句来表示: requires P; 。其中requires是JML关键词,表达的意思是“要求调用者确保P为真”。一个方法规格中可以有多个requires子句,是并列关系,即调用者必须同时满足所有的并列子句要求。其常用来表示传入方法的参数所需要满足的条件。
后置条件(post-condition):后置条件通过ensures子句来表示: ensures P; 。其中ensures是JML关键词,表达的意思是“方法实现者确保方法执 行返回结果一定满足谓词P的要求,即确保P为真”。一个方法规格中可以有多个ensures子句,是并列关系,即方法实现者必须同时满足有所并列ensures子句的要求。其常用来描述该方法的作用,是方法规格中最重要的一部分。
副作用范围限定(side-effects):副作用指方法在执行过程中会修改对象的属性数据或者类的静态成员数据,从而给后续方法的执行带来影响。从方法 规格的角度,必须要明确给出副作用范围。JML提供了副作用约束子句,使用关键词 assignable 或者 modifiable 。其常用来告知读者方法更改了哪些量,方便多人协作交互与bug修复。
由于方法中的行为除了通常的行为,还常常包括抛出异常,故JML还有public normal_behavior和signals子句来表示方法的行为。
public normal_behavior:该关键字表示接下来的部分是对正常的功能的规格,即异常功能之外的功能。
signals子句:signals子句的结构为 signals (***Exception e) b_expr ,意思是当 b_expr 为 true 时,方法会抛出括号中给出 的相应异常e,用于描述异常功能。
类型规格
类型规格指针对Java程序中定义的数据类型所设计的限制规则,一般而言,就是指针对类或接口所设计的约束规则,常见的有不变式限制和约束限制。
不变式invariant:不变式(invariant)是要求在所有可见状态下都必须满足的特性,语法上定义 invariant P ,其中 invariant 为关 键词, P 为谓词。不变式的作用是保证对象在任何时刻的状态都应该是满足不变式的要求。
状态变化约束constraint:状态变化约束本质上也是一种不变式,其也可以看作是对诸多后置条件的简单整合代替。
JML工具
OPENJML:用来检测JML规格是否合乎语法,如对第九次作业的开源代码,会得到
java/com/oocourse/specs1/models/PathContainer.java:66: error: A \old token with no label may not be present in a requires clause
@ requires path != null && path.isValid() && \old(containsPath(path));
^
java/com/oocourse/specs1/models/PathContainer.java:82: error: A \old token with no label may not be present in a requires clause
@ requires \old(containsPathId(pathId));
^
2 errors
然而本单元主要是对着老师写的规格写代码,所以并没有太大的作用。
JUNIT:JUNIT是单元测试工具,可以自动生成对方法的测试文件来实现对方法的检查。
基于JMLUNITNG自动生成测试用例
测试代码
生成的文件
执行结果
Passed: racEnabled()
Passed: constructor Demo()
Passed: static getMax(-2147483648, -2147483648, -2147483648)
Passed: static getMax(0, -2147483648, -2147483648)
Passed: static getMax(2147483648, -2147483648, -2147483648)
Passed: static getMax(-2147483648, 0, -2147483648)
Passed: static getMax(0, 0, -2147483648)
Passed: static getMax(2147483648, 0, -2147483648)
Passed: static getMax(-2147483648, 2147483648, -2147483648)
Passed: static getMax(0, 2147483648, -2147483648)
Passed: static getMax(2147483648, 2147483648, -2147483648)
Passed: static getMax(-2147483648, -2147483648, 0)
Passed: static getMax(0, -2147483648, 0)
Passed: static getMax(2147483648, -2147483648, 0)
Passed: static getMax(-2147483648, 0, 0)
Passed: static getMax(0, 0, 0)
Passed: static getMax(2147483648, 0, 0)
Passed: static getMax(-2147483648, 2147483648, 0)
Passed: static getMax(0, 2147483648, 0)
Passed: static getMax(2147483648, 2147483648, 0)
Passed: static getMax(-2147483648, -2147483648, 2147483648)
Passed: static getMax(0, -2147483648, 2147483648)
Passed: static getMax(2147483648, -2147483648, 2147483648)
Passed: static getMax(-2147483648, 0, 2147483648)
Passed: static getMax(0, 0, 2147483648)
Passed: static getMax(2147483648, 0, 2147483648)
Passed: static getMax(-2147483648, 2147483648, 2147483648)
Passed: static getMax(0, 2147483648, 2147483648)
Passed: static getMax(2147483648, 2147483648, 2147483648)
Passed: static main(null)
Passed: static main({})
可以看出,是对int的边界以及非法数据等进行测试。
架构设计分析
第一次作业分析:
本单元的第一次作业为根据老师写的规格去实现简单的功能。总的来说比较简单,唯一的坑点是会卡CPU时间,如果采用arraylist的话会被爆掉,hashmap为一种比较合理的方法。在方法中,有着path到pathid和pathid到path的双向查找,故我采用了两个hashmap来分别存储path与pathid的对应关系和pathid到path的对应关系。
类图如下:
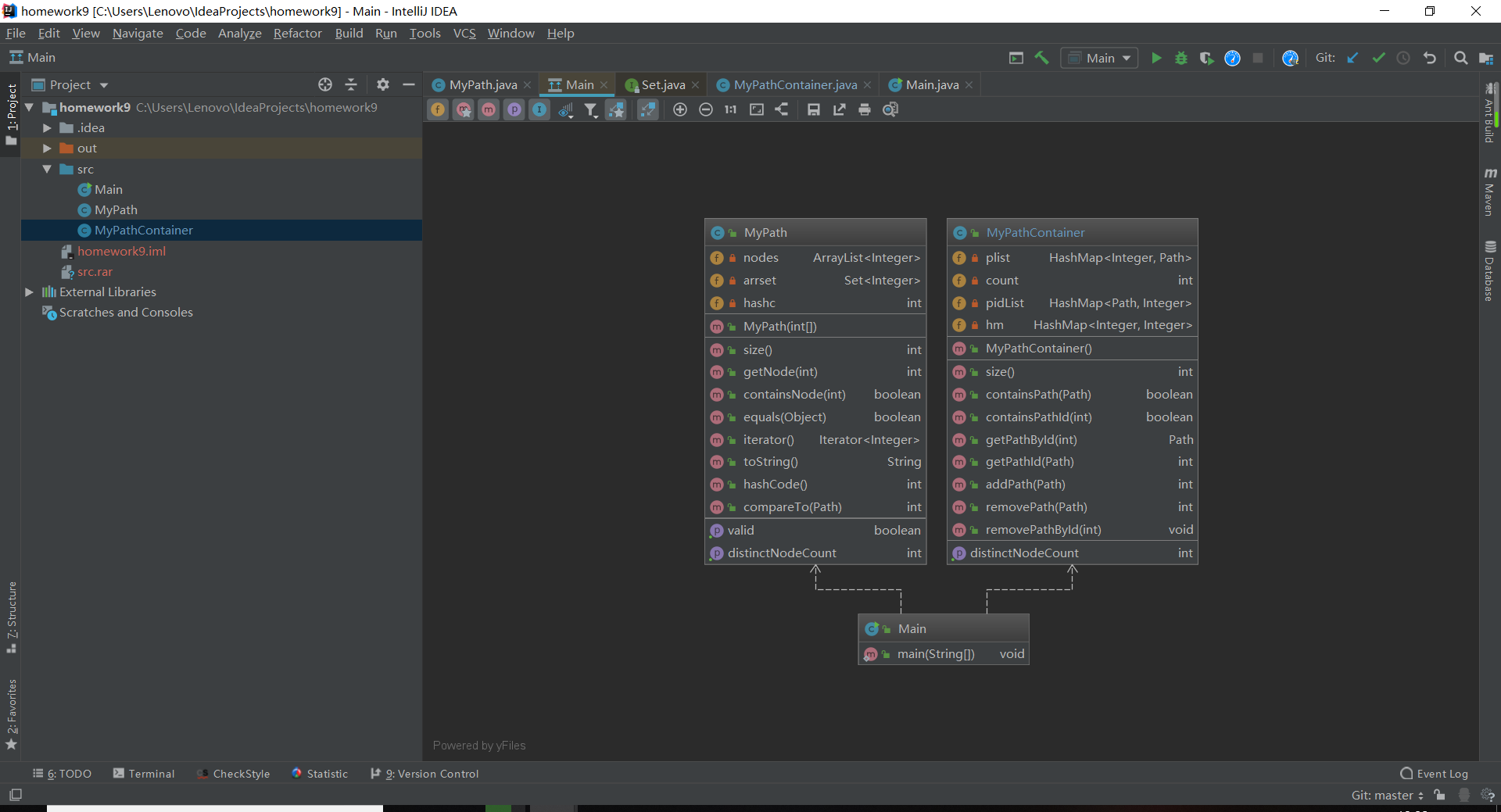
复杂度如下:
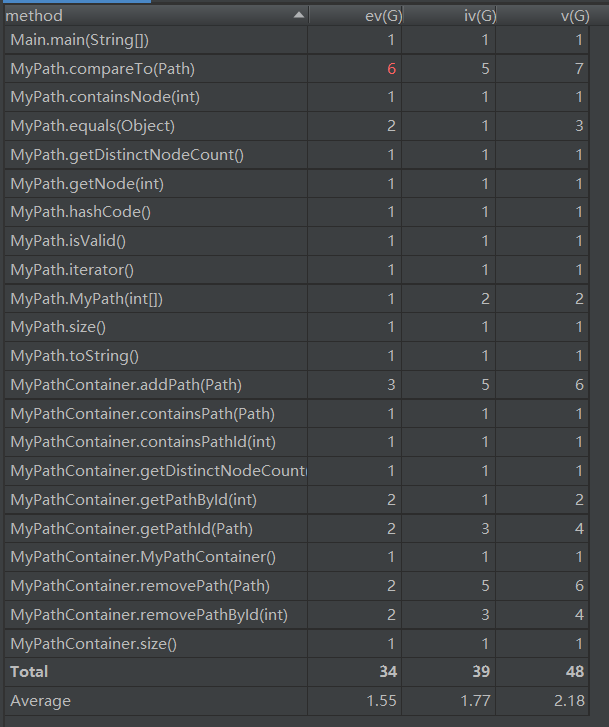

可以看出,第一次作业的结构非常的简单,方法的复杂度也很低。
第二次作业:
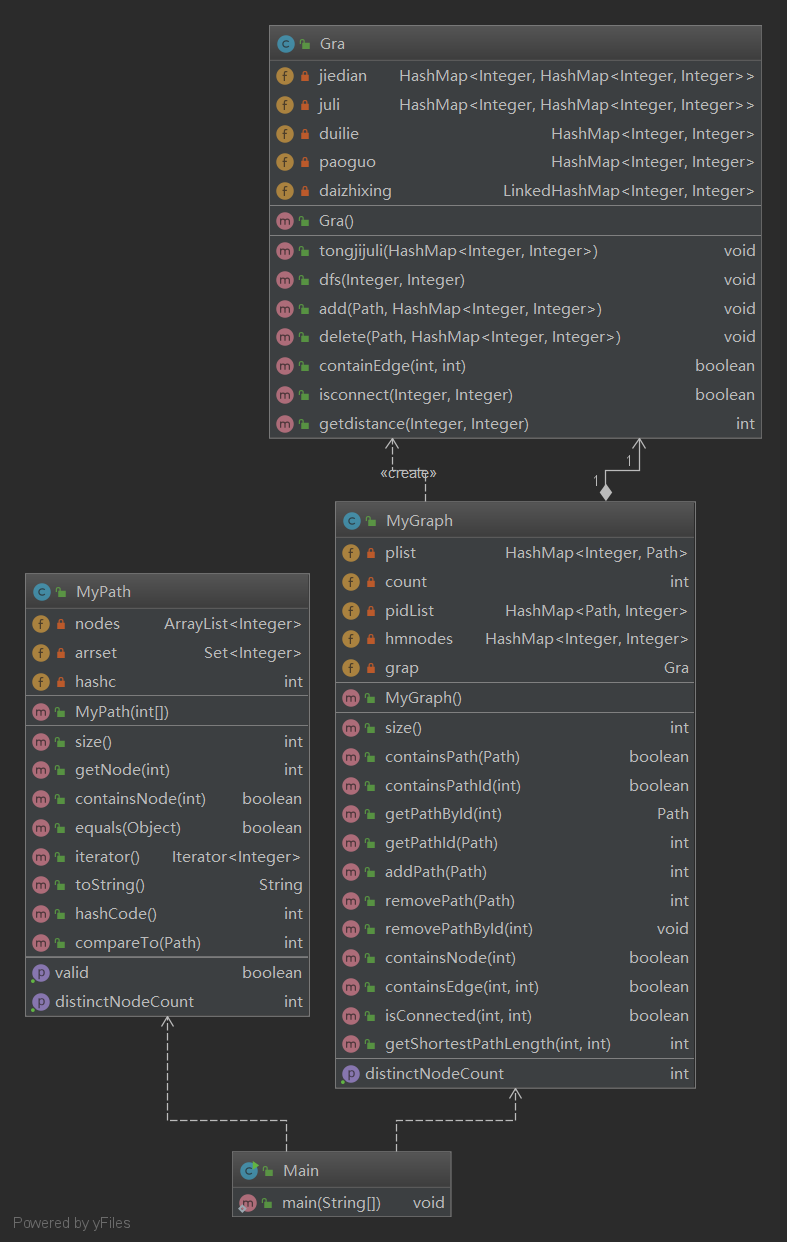
第二次作业在第一次作业的基础上还增加了图的结构,需要我们将输入的路径构建成图并对图进行遍历统计连接关系和最短距离。为了图的构建以及对图的处理,我新建了一个类来存储和处理图。对这个图的存储我采用了HashMap<Integer,HashMap<Integer,Integer>的结构,用来存储当前结点和临接结点的连接情况以及次数,方便增加与删除。由于图的变更指令很少,大多数都为查找指令,所以,我在每一次图的 增删之后都重新统计了每两个结点间的最短距离并且采用HashMap<Integer,HashMap<Integer,Integer>的数据结构来存储两个结点间的最小距离。在查询结点是否连接和结点间最少距离的时候,都可以直接来读取这个数据结构直接得到结果。在对于 最小距离对的统计方面,由于结点构成的是不带权的图,故我才采取了最简单直接的 BFS算法,每次查询到每一个结点,如果没有统计过就将其增加到存储距离的结构中,距离存储为他的父亲结点+1。
类图如下:
复杂度分析如下:
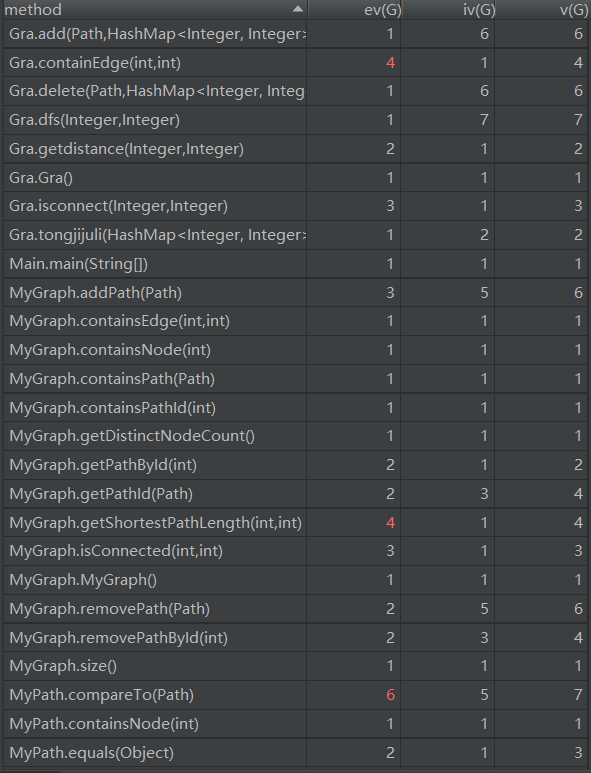
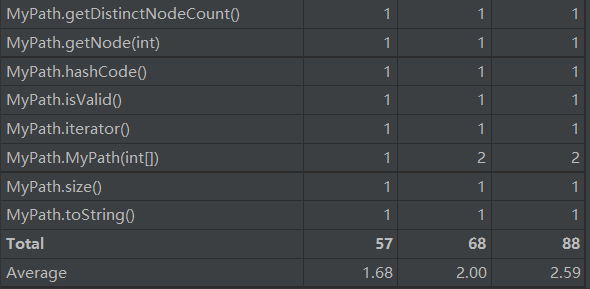
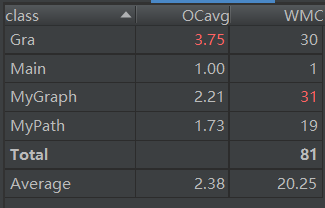
可以看出,这次作业的结构也并不复杂,但是有着许多对于图的操作,需要我们回忆起数据结构学习的相关内容和算法。
第三次作业:
第三次作业是一个比较复杂的地铁系统,是在前两次作业的基础上,增加了统计最短换乘次数,统计最短票价和统计最少不满意度的操作。关键就在于要求我们在构建图的同时将其属于哪一条路径等信息都记录下来并参与复杂的计算。关于本次作业,我有过几种想法。第一种想法拆点+迪杰斯特拉。这种算法对的核心是将被多条path经过的结点拆分成为多个结点,如统计换乘的时候,将每条路径中的结点间的路径权设置为0,将相同节点但是不同路径的看作不同的结点并赋予权值1,这样通过迪杰斯特拉算法求解出的最短路径就是最少的换乘次数;统计最短票价,将每条路径中的结点路径权值设置为1,相同结点但路径不同的看作多个结点并设置权值为2,这样通过迪杰斯特拉算法求出的最短路径就是最少票价;统计最少不满意度,将每条路径中的结点的权值按照不满意度的计算方式赋值,相同结点不同路径拆分成不同的结点并赋予权值32,用迪杰斯特拉求出的最短距离就是最少不满意度。这种做法最大的缺陷我认为是会将一个结点拆分为非常多的结点,导致边数非常多,CPU时间会被炸死掉,同时还要构建三个新的图,每一次增删进行三次迪杰斯特拉。另一种想法是采用优先队列+BFS,基本思想是再创建一个HashMap<Integer,HashMap<Integer,HashMap<Integer,Integer>>的结构,用来存储结点间的连接关系以及路径(最里层的HashMap是为了存储路径信息,同一条边可以在多个路径里面出现。再遍历的时候,采取优先队列+BFS,重写优先队列的比较器用来区分换乘、票价以及不满意度。由于考虑到不像之前的统计距离第一次查找到就是需要的值,就算统计到了最小值,但它对其他结点的贡献并不一定是最小的,也就是说,对于跑的每一个结点,除了要统计下结点的id,还要带着该结点跑过的路径以及当前路径下的最短换乘or最少票价or最少不满意度,也就是说,对于进入优先队列的结点要进行严格的限制,既不能让它回头,又不能让它跑过一次就放弃其他的。第三种想法是弗洛伊德,然而助教在群里面说不行,我就放弃了(然而采用了佛洛依德的同学们写的又快,结果又正确,性能还好????????)我最终采取的是第二种想法。
类图如下:
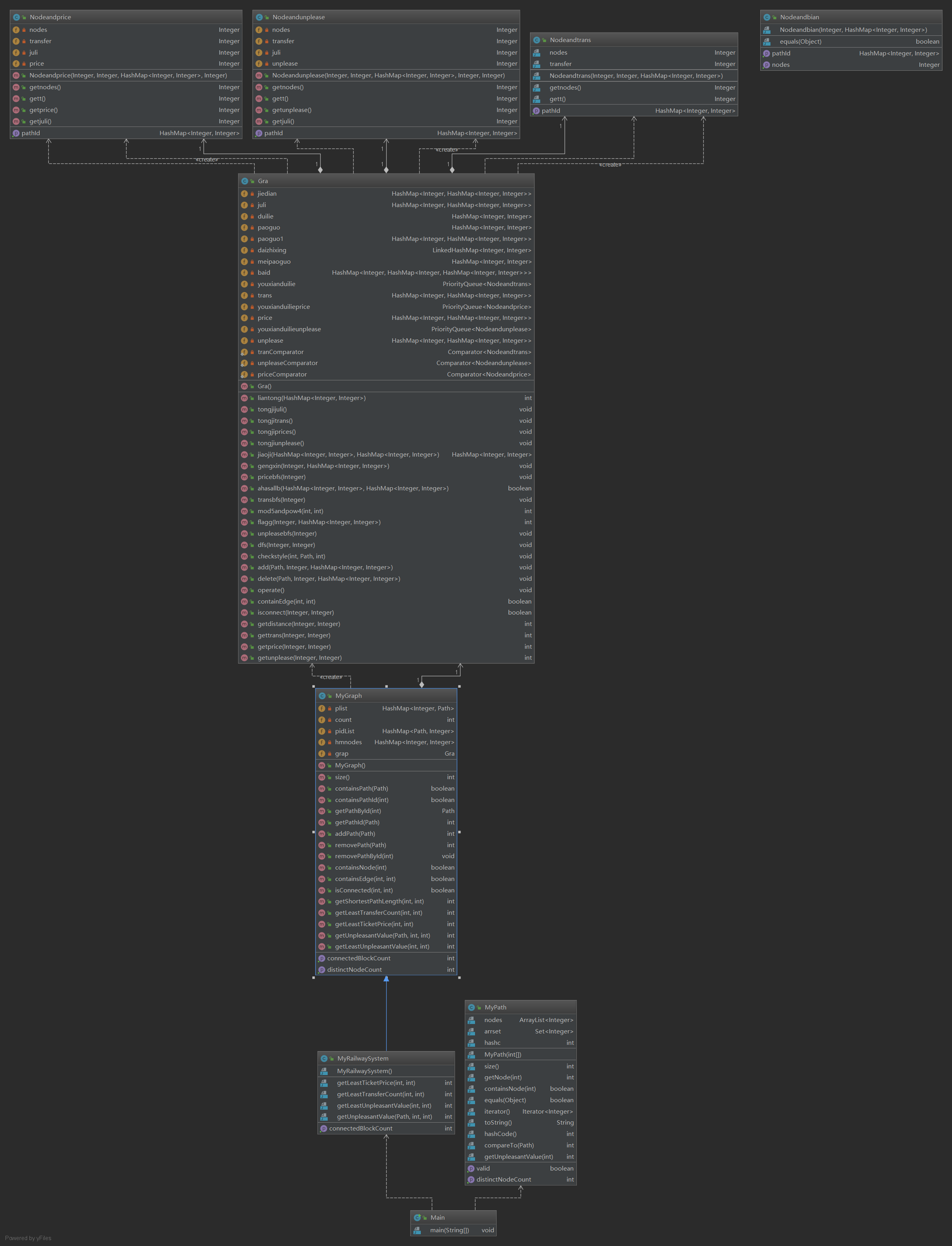
复杂度如下:
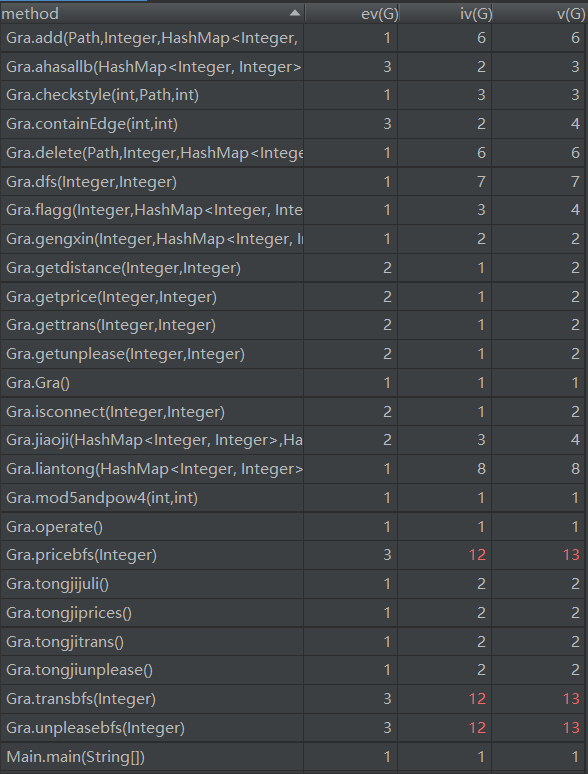
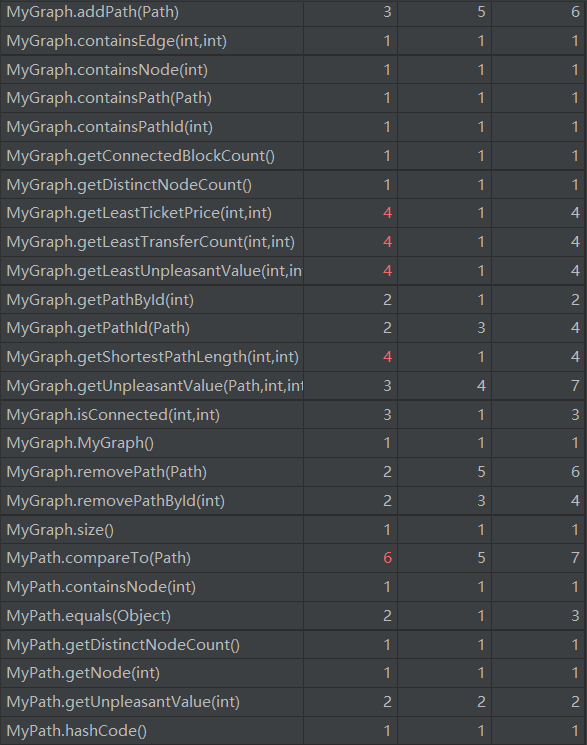
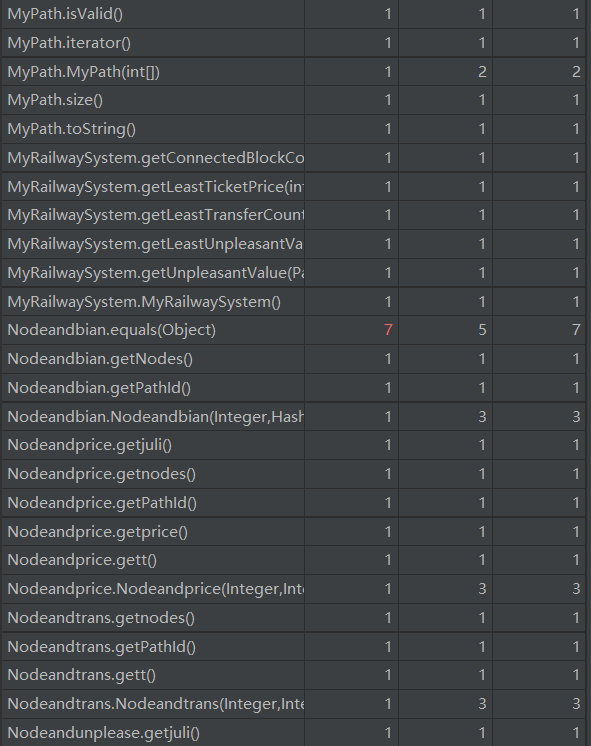
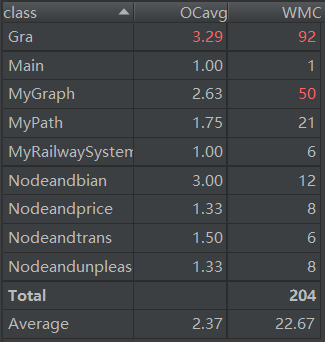
可以看出,方法的复杂度都挺高,结构比较复杂,比较难实现,在我看来比电梯第三次作业甚至更难,数据结构还债课石锤了。
BUG情况
第一次作业:由于非常简单,大家写的基本都一样,一目了然,基本都没什么bug。极度自信甚至膨胀。
第二次作业:我认为第二次作业其实也非常简单,然而,我在对于判断结点是否相连的时候忘记了判断结点是否存在,在我自己构造数据测试的时候也主要是去针对正确性,也忽略掉了这一个点。然而中测也并没有设置这一个点,而强测却不停地炸这一个点,导致全面崩盘爆零,成功没进去互测,虽然我在使用其他同学地从测试数据的时候都没出现过其他的的bug。爆零开始,心情沮丧。
第三次作业:想了很多,尝试了很多,最终选择了一种贼复杂的结构,写道自己崩溃,改了不知道多少次,千方百计满足中测,写了整整四天,然后最后还是遗留下来了bug。我认为我遇到的bug主要就是优先队列的进出限制。我自己也可以构造出多环,大环的长数据就可以轻松陷入死循环;剧烈的前摇(只第一次遇到短的但从它出发导致结果不是最短)也可以得到错误的结果。
事实证明,陪伴写代码全过程的青梅竹马(中测)根本敌不过天降(强测),他们就算看起来有关系,但喜好完全不同,用对待青梅竹马的那一套对待天降是不可能生效的。
规格单元的心得体会
使用规格,可以将方法的作用采用严密的逻辑表述出来,有利于其他人对代码进行理解,也有益于构建测试样例,有利于多人协作。但是对于第三次作业那样的复杂代码,老师用来描述规格就又构建了许多函数,这导致规格复杂难懂,花费大量时间去研究规格反而起不到什么良好的作用,我基本上都是忽略规格直接盲上,再加之数据结构留下的坑以及学艺不精,强测基本全面爆炸。
总之,这一单元的体验就是上机和第一次作业体验极佳,到第二次作业由于疏忽心态开始崩盘,到第三次作业彻底崩溃。




