Trie（前缀树/字典树）及其应用

 Trie，又经常叫前缀树，字典树等等。它有很多变种，如后缀树，Radix Tree/Trie，PATRICIA tree，以及bitwise版本的crit-bit tree。当然很多名字的意义其实有交叉。

 

定义

在计算机科学中，trie，又称前缀树或字典树，是一种有序树，用于保存关联数组，其中的键通常是字符串。与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

trie中的键通常是字符串，但也可以是其它的结构。trie的算法可以很容易地修改为处理其它结构的有序序列，比如一串数字或者形状的排列。比如，bitwise trie中的键是一串位元，可以用于表示整数或者内存地址

 

基本性质

1，根节点不包含字符，除根节点意外每个节点只包含一个字符。

2，从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

3，每个节点的所有子节点包含的字符串不相同。

 

优点：

可以最大限度地减少无谓的字符串比较，故可以用于词频统计和大量字符串排序。

　　跟哈希表比较：

　　　　1，最坏情况时间复杂度比hash表好

　　　　2，没有冲突，除非一个key对应多个值（除key外的其他信息）

　　　　3，自带排序功能（类似Radix Sort），中序遍历trie可以得到排序。

缺点：

1，虽然不同单词共享前缀，但其实trie是一个以空间换时间的算法。其每一个字符都可能包含至多字符集大小数目的指针（不包含卫星数据）。

每个结点的子树的根节点的组织方式有几种。1>如果默认包含所有字符集，则查找速度快但浪费空间（特别是靠近树底部叶子）。2>如果用链接法(如左儿子右兄弟)，则节省空间但查找需顺序（部分）遍历链表。3>alphabet reduction: 减少字符宽度以减少字母集个数。,4>对字符集使用bitmap，再配合链接法。

2，如果数据存储在外部存储器等较慢位置，Trie会较hash速度慢（hash访问O(1)次外存，Trie访问O(树高)）。

3，长的浮点数等会让链变得很长。可用bitwise trie改进。

 

bit-wise Trie

类似于普通的Trie，但是字符集为一个bit位，所以孩子也只有两个。

可用于地址分配，路由管理等。

虽然是按bit位存储和判断，但因为cache-local和可高度并行，所以性能很高。跟红黑树比，红黑树虽然纸面性能更高，但是因为cache不友好和串行运行多，瓶颈在存储访问延迟而不是CPU速度。

 

压缩Trie

压缩分支条件：

1，Trie基本不变

2，只是查询

3，key跟结点的特定数据无关

4，分支很稀疏

若允许添加和删除，就可能需要分裂和合并结点。此时可能需要对压缩率和更新（裂，并）频率进行折中。

 

外存Trie

某些变种如后缀树适合存储在外部，另外还有B-trie等。

 

应用场景：

（1） 字符串检索
事先将已知的一些字符串（字典）的有关信息保存到trie树里，查找另外一些未知字符串是否出现过或者出现频率。
举例：
1，给出N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，请你按最早出现的顺序写出所有不在熟词表中的生词。
2，给出一个词典，其中的单词为不良单词。单词均为小写字母。再给出一段文本，文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如，若rob是不良单词，那么文本problem含有不良单词。

3，1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。

 

（2）文本预测、自动完成，see also，拼写检查

 

（3）词频统计

1，有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

2，一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。

3，寻找热门查询：搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录，这些查询串的重复度比较高，虽然总数是1千万，但是如果去除重复，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就越热门。请你统计最热门的10个查询串，要求使用的内存不能超过1G。
(1) 请描述你解决这个问题的思路；
(2) 请给出主要的处理流程，算法，以及算法的复杂度。

==》若无内存限制：Trie + “k-大/小根堆”（k为要找到的数目）。

否则，先hash分段再对每一个段用hash（另一个hash函数）统计词频，再要么利用归并排序的某些特性（如partial_sort），要么利用某使用外存的方法。参考

　　“海量数据处理之归并、堆排、前K方法的应用：一道面试题” http://www.dataguru.cn/thread-485388-1-1.html。

　　“算法面试题之统计词频前k大” http://blog.csdn.net/u011077606/article/details/42640867

　　 算法导论笔记——第九章 中位数和顺序统计量 

 

（4）排序

Trie树是一棵多叉树，只要先序遍历整棵树，输出相应的字符串便是按字典序排序的结果。
比如给你N 个互不相同的仅由一个单词构成的英文名，让你将它们按字典序从小到大排序输出。

 

（5）字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间，当我们把大量字符串存储到一棵trie树上时，我们可以快速得到某些字符串的公共前缀。
举例：
给出N 个小写英文字母串，以及Q 个询问，即询问某两个串的最长公共前缀的长度是多少？
解决方案：首先对所有的串建立其对应的字母树。此时发现，对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数，于是，问题就转化为了离线（Offline）的最近公共祖先（Least Common Ancestor，简称LCA）问题。
而最近公共祖先问题同样是一个经典问题，可以用下面几种方法：
1. 利用并查集（Disjoint Set），可以采用采用经典的Tarjan 算法；
2. 求出字母树的欧拉序列（Euler Sequence ）后，就可以转为经典的最小值查询（Range Minimum Query，简称RMQ）问题了；

 

（6）字符串搜索的前缀匹配
trie树常用于搜索提示。如当输入一个网址，可以自动搜索出可能的选择。当没有完全匹配的搜索结果，可以返回前缀最相似的可能。
Trie树检索的时间复杂度可以做到n，n是要检索单词的长度，
如果使用暴力检索，需要指数级O(n2)的时间复杂度。

 

（7） 作为其他数据结构和算法的辅助结构
如后缀树，AC自动机等

后缀树可以用于全文搜索

 

转一篇关于几种Trie速度比较的文章：http://www.hankcs.com/nlp/performance-comparison-of-several-trie-tree.html

Trie树和其它数据结构的比较 http://www.raychase.net/1783

 

参考：

[1] 维基百科：Trie， https://en.wikipedia.org/wiki/Trie

[2] LeetCode字典树(Trie)总结， http://www.jianshu.com/p/bbfe4874f66f

[3] 字典树(Trie树)的实现及应用， http://www.cnblogs.com/binyue/p/3771040.html#undefined

[4] 6天通吃树结构—— 第五天 Trie树， http://www.cnblogs.com/huangxincheng/archive/2012/11/25/2788268.html

 

 

 

 =============摘录自维基百科============

In computer science, a trie, also called digital tree and sometimes radix tree or prefix tree (as they can be searched by prefixes), is a kind of search tree—an ordered tree data structure that is used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Values are not necessarily associated with every node. Rather, values tend only to be associated with leaves, and with some inner nodes that correspond to keys of interest. For the space-optimized presentation of prefix tree, see compact prefix tree.

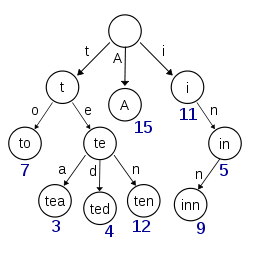
A trie for keys "A","to", "tea", "ted", "ten", "i", "in", and "inn".

In the example shown, keys are listed in the nodes and values below them. Each complete English word has an arbitrary integer value associated with it. A trie can be seen as a tree-shaped deterministic finite automaton. Each finite language is generated by a trie automaton, and each trie can be compressed into a deterministic acyclic finite state automaton.

Though tries are usually keyed by character strings,[not verified in body] they need not be. The same algorithms can be adapted to serve similar functions of ordered lists of any construct, e.g. permutations on a list of digits or shapes. In particular, a bitwise trie is keyed on the individual bits making up any fixed-length binary datum, such as an integer or memory address.[citation needed]

Contents

History and etymology

Tries were first described by René de la Briandais in 1959.[1][2]:336 The term trie was coined two years later by Edward Fredkin, who pronounces it /ˈtriː/ (as "tree"), after the middle syllable of retrieval.[3][4]However, other authors pronounce it /ˈtraɪ/ (as "try"), in an attempt to distinguish it verbally from "tree".[3][4][5]

Applications

As a replacement for other data structures

As discussed below, a trie has a number of advantages over binary search trees.[6] A trie can also be used to replace a hash table, over which it has the following advantages:

  • Looking up data in a trie is faster in the worst case, O(m) time (where m is the length of a search string), compared to an imperfect hash table. An imperfect hash table can have key collisions. A key collision is the hash function mapping of different keys to the same position in a hash table. The worst-case lookup speed in an imperfect hash table is O(N) time, but far more typically is O(1), with O(m) time spent evaluating the hash.[citation needed]
  • There are no collisions of different keys in a trie.
  • Buckets in a trie, which are analogous to hash table buckets that store key collisions, are necessary only if a single key is associated with more than one value.[citation needed]
  • There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
  • A trie can provide an alphabetical ordering of the entries by key.

Tries do have some drawbacks as well:

  • Tries can be slower in some cases than hash tables for looking up data, especially if the data is directly accessed on a hard disk drive or some other secondary storage device where the random-access time is high compared to main memory.[7]
  • Some keys, such as floating point numbers, can lead to long chains and prefixes that are not particularly meaningful. Nevertheless, a bitwise trie can handle standard IEEE single and double format floating point numbers.[citation needed]
  • Some tries can require more space than a hash table, as memory may be allocated for each character in the search string, rather than a single chunk of memory for the whole entry, as in most hash tables.

Dictionary representation

A common application of a trie is storing a predictive text or autocomplete dictionary, such as found on a mobile telephone. Such applications take advantage of a trie's ability to quickly search for, insert, and delete entries; however, if storing dictionary words is all that is required (i.e., storage of information auxiliary to each word is not required), a minimal deterministic acyclic finite state automaton (DAFSA) would use less space than a trie. This is because a DAFSA can compress identical branches from the trie which correspond to the same suffixes (or parts) of different words being stored.

Tries are also well suited for implementing approximate matching algorithms,[8] including those used in spell checking and hyphenation[4] software.

Term indexing

A discrimination tree term index stores its information in a trie data structure.[9]

Algorithms

Lookup and membership are easily described. The listing below implements a recursive trie node as a Haskell data type. It stores an optional value and a list of children tries, indexed by the next character:

import Data.Map
 
data Trie a = Trie { value    :: Maybe a,
                     children :: Map Char (Trie a) }

We can look up a value in the trie as follows:

find :: String -> Trie a -> Maybe a
find []     t = value t
find (k:ks) t = do
  ct <- Data.Map.lookup k (children t)
  find ks ct

In an imperative style, and assuming an appropriate data type in place, we can describe the same algorithm in Python (here, specifically for testing membership). Note that children is a list of a node's children; and we say that a "terminal" node is one which contains a valid word.

def find(node, key):
    for char in key:
        if char in node.children:
            node = node.children[char]
        else:
            return None
    return node.value == key

Insertion proceeds by walking the trie according to the string to be inserted, then appending new nodes for the suffix of the string that is not contained in the trie. In imperative Pascal pseudocode:

algorithm insert(root : node, s : string, value : any):
    node = root
    i    = 0
    n    = length(s)

    while i < n:
        if node.child(s[i]) != nil:
            node = node.child(s[i])
            i = i + 1
        else:
            break

    (* append new nodes, if necessary *)
    while i < n:
        node.child(s[i]) = new node
        node = node.child(s[i])
        i = i + 1

    node.value = value

Sorting

Lexicographic sorting of a set of keys can be accomplished with an inorder traversal over trie.

This algorithm is a form of radix sort.

A trie forms the fundamental data structure of Burstsort, which (in 2007) was the fastest known string sorting algorithm.[10] However, now there are faster string sorting algorithms.[11]

Full text search

A special kind of trie, called a suffix tree, can be used to index all suffixes in a text in order to carry out fast full text searches.

Implementation strategies

 
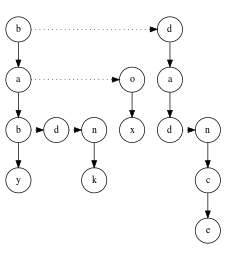
A trie implemented as a doubly chained tree: vertical arrows are child pointers, dashed horizontal arrows are next pointers. The set of strings stored in this trie is {baby, bad, bank, box, dad, dance}. The lists are sorted to allow traversal in lexicographic order.

There are several ways to represent tries, corresponding to different trade-offs between memory use and speed of the operations. The basic form is that of a linked set of nodes, where each node contains an array of child pointers, one for each symbol in the alphabet (so for the English alphabet, one would store 26 child pointers and for the alphabet of bytes, 256 pointers). This is simple but wasteful in terms of memory: using the alphabet of bytes (size 256) and four-byte pointers, each node requires a kilobyte of storage, and when there is little overlap in the strings' prefixes, the number of required nodes is roughly the combined length of the stored strings.[2]:341 Put another way, the nodes near the bottom of the tree tend to have few children and there are many of them, so the structure wastes space storing null pointers.[12]

The storage problem can be alleviated by an implementation technique called alphabet reduction, whereby the original strings are reinterpreted as longer strings over a smaller alphabet. E.g., a string of n bytes can alternatively be regarded as a string of 2n four-bit units and stored in a trie with sixteen pointers per node. Lookups need to visit twice as many nodes in the worst case, but the storage requirements go down by a factor of eight.[2]:347–352

An alternative implementation represents a node as a triple (symbol, child, next) and links the children of a node together as a singly linked list: child points to the node's first child, next to the parent node's next child.[12][13] The set of children can also be represented as a binary search tree; one instance of this idea is the ternary search tree developed by Bentley and Sedgewick.[2]:353

Another alternative in order to avoid the use of an array of 256 pointers (ASCII), as suggested before, is to store the alphabet array as a bitmap of 256 bits representing the ASCII alphabet, reducing dramatically the size of the nodes.[14]

Bitwise tries
This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (February 2015) (Learn how and when to remove this template message)

Bitwise tries are much the same as a normal character-based trie except that individual bits are used to traverse what effectively becomes a form of binary tree. Generally, implementations use a special CPU instruction to very quickly find the first set bit in a fixed length key (e.g., GCC's __builtin_clz() intrinsic). This value is then used to index a 32- or 64-entry table which points to the first item in the bitwise trie with that number of leading zero bits. The search then proceeds by testing each subsequent bit in the key and choosing child[0] or child[1] appropriately until the item is found.

Although this process might sound slow, it is very cache-local and highly parallelizable due to the lack of register dependencies and therefore in fact has excellent performance on modern out-of-order execution CPUs. A red-black tree for example performs much better on paper, but is highly cache-unfriendly and causes multiple pipeline and TLB stalls on modern CPUs which makes that algorithm bound by memory latency rather than CPU speed. In comparison, a bitwise trie rarely accesses memory, and when it does, it does so only to read, thus avoiding SMP cache coherency overhead. Hence, it is increasingly becoming the algorithm of choice for code that performs many rapid insertions and deletions, such as memory allocators (e.g., recent versions of the famous Doug Lea's allocator (dlmalloc) and its descendents).

Compressing tries

Compressing the trie and merging the common branches can sometimes yield large performance gains. This works best under the following conditions:

  • The trie is mostly static (key insertions to or deletions from a pre-filled trie are disabled).[citation needed]
  • Only lookups are needed.
  • The trie nodes are not keyed by node-specific data, or the nodes' data are common.[15]
  • The total set of stored keys is very sparse within their representation space.[citation needed]

For example, it may be used to represent sparse bitsets, i.e., subsets of a much larger, fixed enumerable set. In such a case, the trie is keyed by the bit element position within the full set. The key is created from the string of bits needed to encode the integral position of each element. Such tries have a very degenerate form with many missing branches. After detecting the repetition of common patterns or filling the unused gaps, the unique leaf nodes (bit strings) can be stored and compressed easily, reducing the overall size of the trie.

Such compression is also used in the implementation of the various fast lookup tables for retrieving Unicode character properties. These could include case-mapping tables (e.g. for the Greek letter pi, from ∏ to π), or lookup tables normalizing the combination of base and combining characters (like the a-umlaut in German, ä, or the dalet-patah-dagesh-ole in Biblical Hebrew, דַּ֫‎). For such applications, the representation is similar to transforming a very large, unidimensional, sparse table (e.g. Unicode code points) into a multidimensional matrix of their combinations, and then using the coordinates in the hyper-matrix as the string key of an uncompressed trie to represent the resulting character. The compression will then consist of detecting and merging the common columns within the hyper-matrix to compress the last dimension in the key. For example, to avoid storing the full, multibyte Unicode code point of each element forming a matrix column, the groupings of similar code points can be exploited. Each dimension of the hyper-matrix stores the start position of the next dimension, so that only the offset (typically a single byte) need be stored. The resulting vector is itself compressible when it is also sparse, so each dimension (associated to a layer level in the trie) can be compressed separately.

Some implementations do support such data compression within dynamic sparse tries and allow insertions and deletions in compressed tries. However, this usually has a significant cost when compressed segments need to be split or merged. Some tradeoff has to be made between data compression and update speed. A typical strategy is to limit the range of global lookups for comparing the common branches in the sparse trie.[citation needed]

The result of such compression may look similar to trying to transform the trie into a directed acyclic graph (DAG), because the reverse transform from a DAG to a trie is obvious and always possible. However, the shape of the DAG is determined by the form of the key chosen to index the nodes, in turn constraining the compression possible.

Another compression strategy is to "unravel" the data structure into a single byte array.[16] This approach eliminates the need for node pointers, substantially reducing the memory requirements. This in turn permits memory mapping and the use of virtual memory to efficiently load the data from disk.

One more approach is to "pack" the trie.[4] Liang describes a space-efficient implementation of a sparse packed trie applied to automatic hyphenation, in which the descendants of each node may be interleaved in memory.

External memory tries

Several trie variants are suitable for maintaining sets of strings in external memory, including suffix trees. A combination of trie and B-tree, called the B-trie has also been suggested for this task; compared to suffix trees, they are limited in the supported operations but also more compact, while performing update operations faster.[17]

See also

References

  1. Askitis, Nikolas; Zobel, Justin (2008). "B-tries for Disk-based String Management" (PDF). VLDB Journal: 1–26. ISSN 1066-8888.

External links

Wikimedia Commons has media related to Trie.
Look up trie in Wiktionary, the free dictionary.
posted on 2013-05-03 11:10  duanxz  阅读(896)  评论(0)  编辑  收藏  举报

Powered by: 博客园 Copyright © 2024 duanxz
Powered by .NET 9.0 on Kubernetes