机器学习之线性回归

背景

本文是我在学习 Andrew Ng 的机器学习课程的总结

简介

作为本系列的第一讲，线性模型形式简单，易于建模，但是蕴含着机器学习中一些重要的基本思想。许多功能更为强大的非线性模型可在线性模型的基础上引入层级结构或高维映射而得。此外，线性模型也有比较好的可解释性

例子

让我们从一个经典的例子开始。这个例子是预测住房价格的，我们要使用一个包含俄勒冈州波特兰市的住房价格数据集。我们根据不同房屋尺寸所售出的价格，画出数据集

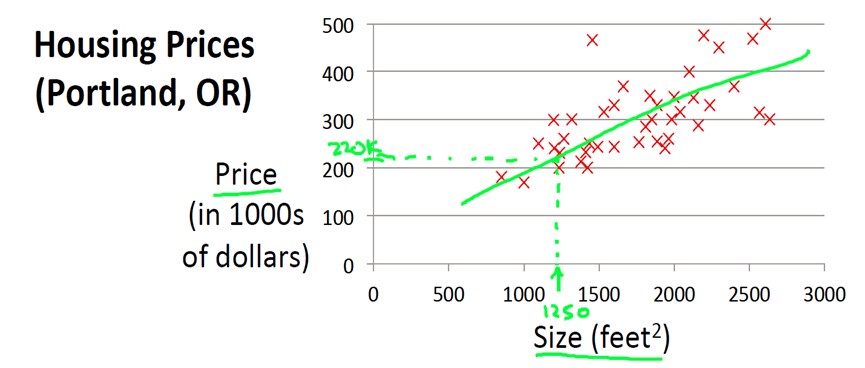
• 横坐标表示房屋尺寸size(\(feet^2\)), 纵轴表示实际价格Prices
• 从图中可以看出如果房屋尺寸为1250平方尺，最终能够以220000美元卖掉

我们如何表达我们的例子呢，我们定义一个函数 h:

\[h(x) = \theta_0x_0 + \theta_1x_1 \]

我们设\(x_0 = 1\), 那么 \(\theta_0\) 表示截距, \(\theta_1\) 表示房屋尺寸, \(h(x)\) 表示 实际售价

名词解释

我们使用 \(x^{(i)}\) 来表示输入变量，也叫做特征,在当前的例子里面是房屋尺寸。\(y^{(i)}\) 表示输出变量，也叫做目标变量，在当前的例子中是房屋的实际出售价格，一对 \((x^{(i)}, y^{(i)})\) 被称作 一个训练样本，一堆的训练样本称为训练集(training set). 我们的目标是通过给定训练集(training set), 去学习一个特征到目标变量映射的函数 \(h: x > y\), 由于历史原因我们把h称为 hypothesis。整个过程如下图

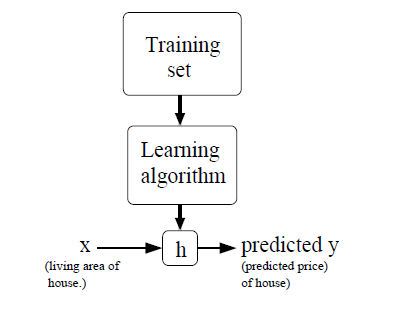
如果我们的目标变量是连续的，我们称之为回归问题，如果是离散的，则称之为分类问题

单变量线性回归

首先，我们来定义一下我们的函数 h:

\[h(x) = \theta_0x_0 + \theta_1x_1 \]

那么给定数据集，我们如何学习参数\(\theta\)呢，一种显而易见的做法是使我们的预测值和真实值尽可能接近，我们使用均方误差来衡量：

\[J(\theta) = \frac{1}{2}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \]

• 其中 m 为样本的个数
  我们称上面的式子为损失函数，我们绘制一个等高线图，三个坐标分别为\(\theta0\) 和 \(\theta1\) 和 J(\(\theta0\),\(\theta1\))：

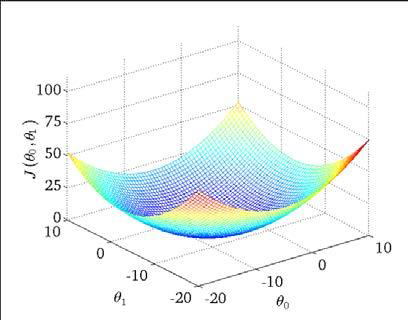
可以看出在三维空间中存在一个使得 J(\(\theta\)) 最小的点,由于损失函数 \(J(\theta)\) 是凸函数，我们的目的是最小化 \(J(\theta)\)， 可以使用的算法有 梯度下降， 最小二乘法， 牛顿法等。

均方误差

让我们从高斯分布的角度使用最大似然法来解释均方误差，首先把我们的假设h写成如下的形式：

\[y^{(i)} = \theta^Tx + \varepsilon^{(i)} \]

• \(\varepsilon\) 表示模型不能表示的误差项

首先有如下几个假设

• 误差 \(\varepsilon\) 是独立同分布的，也即IID (independently and identically distributed), 服从均值为0，方差为某定值的\(\sigma^2\) 的高斯分布
• 样本相互独立

推导步骤如下：

\[p(\varepsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\varepsilon- 0)^2}{2\sigma^2}) \]

\[p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(h_\theta(x^{(i)}) - y^{(i)})^2}{2\sigma^2}) \]

\[\begin{eqnarray*} L(\theta) & = & \prod_{i=1}^m p(\varepsilon^{(i)}) \\ & = & \prod_{i=1}^m \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(h_\theta(x^{(i)}) - y^{(i)})^2}{2\sigma^2}) \end{eqnarray*}\]

\[\begin{eqnarray*} l(\theta) & = & \log L(\theta) \\ & = & \sum_{i=1}^m \log \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(h_\theta(x^{(i)}) - y^{(i)})^2}{2\sigma^2}) \\ & = & \sum_{i=1}^m \log \frac{1}{\sqrt{2\pi}\sigma} - \frac {1}{\sigma^2} \frac {1}{2}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \end{eqnarray*}\]

要最大化上述公式，需要最小化：

\[J(\theta) = \frac{1}{2}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \]

算法

梯度下降法

• 梯度是方向导数的最大值
• 沿着梯度方向是函数值增加最快的方向
• 反方向是函数值下降最快的方向
• 梯度下降法是一种求函数极小值的方法

梯度下降法的公式是：

重复使用下面的算法更新 \(\theta\), 直到收敛 {

\[\theta_j := \theta_j - \alpha \frac{\partial }{\partial \theta_j} J(\theta) \]

}

其中 \(\alpha\) 称为学习率， 他决定了我们沿着能让损失函数下降程度最大的方向下降的步子有多大。
可以从下图看出梯度下降法的执行过程：

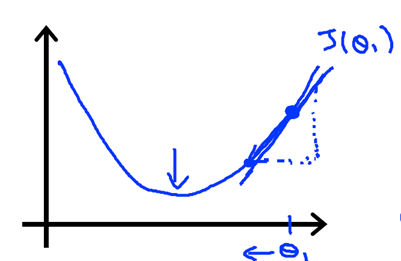
偏导数

我们先推导一下上式右手边的偏导数，在此我们假设只有一个样本数据：

\[\begin{eqnarray*} \frac{\partial }{\partial \theta_j} J(\theta) & = & \frac{\partial }{\partial \theta_j}\frac{1}{2} (h_\theta(x^{(i)}) - y^{(i)})^2\\ & = & \frac{1}{2} 2 (h_\theta(x) - y) \frac{\partial }{\partial \theta_j} (\sum_{i=1}^n \theta_ix_i - y) \\ & = & (h_\theta(x) - y) x_j \end{eqnarray*}\]

所以对于一个样本， 更新规则可以改写为：

\[\theta_j := \theta_j - \alpha (h_\theta(x) - y) x_j \]

学习率 \(\alpha\)

下图展示了学习率的取值不同，算法的收敛速度差异很大：

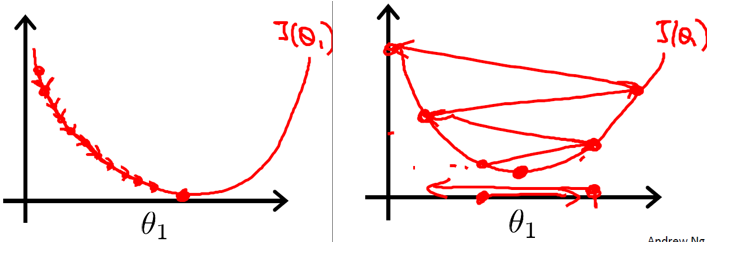
• 对于learning rate(又称为步长)来说，如果过小，梯度下降可能很慢；如果过大，梯度下降有可能“迈过”（overshoot）最小点，并且有可能收敛失败，并且产生“分歧”(diverge)

最小二乘法

由于损失函数是凸函数，最小值在偏导数等于0时取得：

\[\frac{\partial }{\partial \theta_j} J(\theta) = \cdots = 0 \]

多变量线性回归

例子

现在我们对我们开始的房价模型增加更多的特征，例如 房间数， 楼层数， 房龄

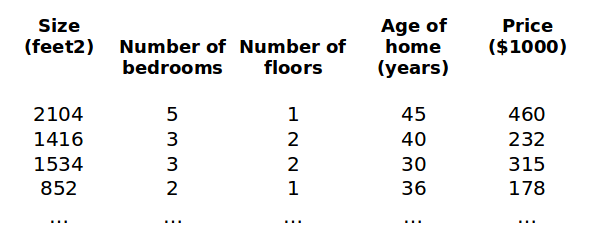
定义我们的函数 h 为

\[h(x) = \theta_0x_0 + \theta_1x_1 + \theta_2x_2 + \cdots + \theta_nx_n \]

• 令 \(x_0 = 1\), 我们可以把 h 向量化成更简单的形式：

\[h(x) = \theta^Tx \]

损失函数

\[J(\theta) = \frac{1}{2}\sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 \]

算法

梯度下降法

前面我们已经求出了单样本单变量下的梯度下降算法， 多样本多变量下的梯度下降算法定义如下：
重复使用下面的算法更新 \(\theta\), 直到收敛 {
$\theta_j := \theta_j - \alpha \sum_{i=1}^m (h_\theta(x) - y) x_j $ (for every j)
}

上述公式在每次更新时，都会使用全量数据集，计算复杂度很高，对于线性回归来说，由于损失函数是严格的凸函数，所以只会有一个全局最小值，如下的优化算法也可以达到很好的效果：

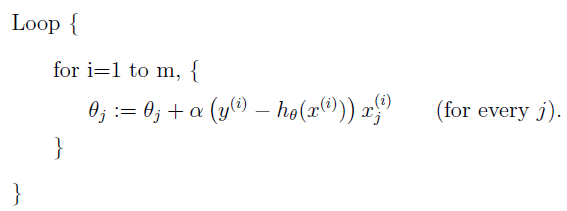
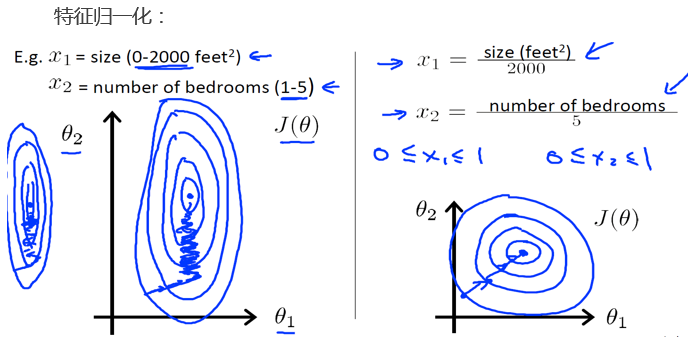
特征归一化

在我们面对包含多维特征的问题的时候，我们需要确保这些特征都有相似的尺度，这将帮助梯度下降算法更快的收敛
以房价问题为例， 假设我们使用两个特征，房屋尺寸和房间数量，尺寸的范围为0~2000平方英尺， 而房间的数量范围时 0~5, 以这两个特征作为横坐标和纵坐标绘制等高线图，可以看出图像很扁，梯度下降算法需要很多次才能收敛

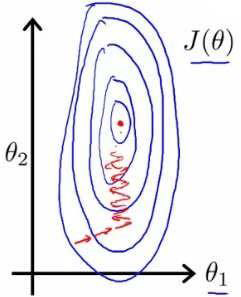
解决的方法是将所有特征的尺度缩放到 -1 ~ 1 之间

最小二乘法

牛顿法

正则

代码实现

python

以下代码在 jupyter中运行

numpy

%matplotlib inline

import numpy as np

x = np.array([0, 1, 2, 3])
y = np.array([-1, 0.2, 0.9, 2.1])

A = np.vstack([x, np.ones(len(x))]).T
m, c = np.linalg.lstsq(A, y)[0]
print(m, c)

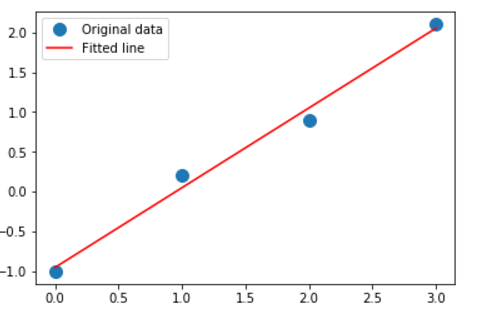
import matplotlib.pyplot as plt
plt.plot(x, y, 'o', label='Original data', markersize=10)
plt.plot(x, m*x + c, 'r', label='Fitted line')
plt.legend()
plt.show()

sklearn

from sklearn import linear_model
clf = linear_model.LinearRegression() # linear_model.LinearRegression(fit_intercept=False)
clf.fit ([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
clf.coef_

r

library(ggplot2)

x <- c(0, 1, 2, 3)
y <- c(-1, 0.2, 0.9, 2.1)
df <- data.frame(x,y)

lr_model <- lm(y ~ x) # lm(y ~ x - 1) # without intercept
summary(lr_model)


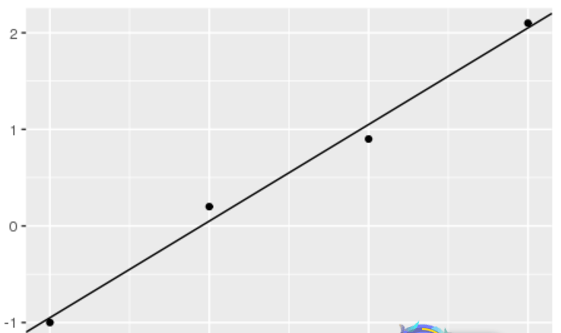
ggplot() + geom_point(aes(x=x, y=y), data=df) + geom_abline(slope=lr_model$coefficients[2], intercept=lr_model$coefficients[1])

java

依赖

<dependency>
     <groupId>org.apache.commons</groupId>
     <artifactId>commons-math3</artifactId>
     <version>3.6.1</version>      
 </dependency>

一元线性回归

regression = new SimpleRegression(); // new SimpleRegression(false); // without intercept
regression.addData(1d, 2d);
regression.addData(3d, 3d);
regression.addData(3d, 3d);
// double[][] data = { { 1, 3 }, {2, 5 }, {3, 7 }, {4, 14 }, {5, 11 }};
// regression.addData(data);

System.out.println(regression.getIntercept());
System.out.println(regression.getSlope());

多元线性回归

OLSMultipleLinearRegression regression = new OLSMultipleLinearRegression();
double[] y = new double[]{11.0, 12.0, 13.0, 14.0, 15.0, 16.0};
double[][] x = new double[6][];
x[0] = new double[]{0, 0, 0, 0, 0};
x[1] = new double[]{2.0, 0, 0, 0, 0};
x[2] = new double[]{0, 3.0, 0, 0, 0};
x[3] = new double[]{0, 0, 4.0, 0, 0};
x[4] = new double[]{0, 0, 0, 5.0, 0};
x[5] = new double[]{0, 0, 0, 0, 6.0};          
regression.newSampleData(y, x);
double[] beta = regression.estimateRegressionParameters();

参考文献

• machine learning Andrew Ng
• 机器学习 周志华