八皇后问题（N皇后问题）

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

首先来看看这张模拟八皇后的图。

这张图说明皇后具有横轴、竖轴以及两个斜轴方向的杀伤力，也就是像米字形一样；

为了减少判断，我们按照一个方向往另一个方向排列，中间不能跳行，这样我们就可以只判断已经有皇后的位置，还没有皇后的就可以偷懒不用判断了。

我的方案是：1.从最下面开始排列，然后往上添加，从左往右排列，这样就只需要判断比自己Y坐标低的具有杀伤能力的位置有没有皇后就OK

　　　　　　　　方法是把自己假定要放置皇后的位置的X和Y轴都依据判断特性进行处理；例如，左斜线X和Y轴都减1；中间的只需要把Y轴减1；右边的和左边的相反，X轴加1，Y轴减1；注意处理边界问题。

　　　　　　2.为了找到合适的位置我们需要在查找失败的时候具备回溯的能力，就需要退回到前一行（Y=Y-1，注意XY是否到边界），直至能回溯或者全部判断完毕，每次回溯的时候记得X轴要从头开始

　　　　　　3.通过一个数据结构记录正在查找的方案，通过另一个数据结构记录已经找到的方案，当然也可以用一个变量记录方案个数

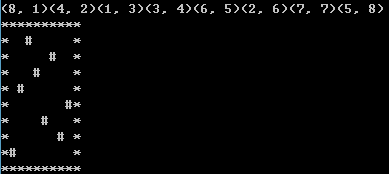
下面这张黑色背景是其中一个方案的截图，第一行代表皇后的坐标xy；后面的是棋盘，这里输出竖轴是x，横轴是y，从上到下，从左到右，其中*是边界，空格是空区，#是皇后。

#include <iostream>
#include <cstring>
#include "DTString.h"
#include "LinkList.h"　　// 这里使用链表存储皇后的位置

using namespace std;
using namespace DTLib;

template <int SIZE>             // N皇后问题，SIZE表示皇后个数或者棋盘大小
class QueenSolution : public Object
{
protected:
    enum { N = SIZE + 2 };      // N表示棋盘大小，为了边界识别，棋盘四周都要加一格

    struct Pos : public Object  // 方位结构体
    {
        Pos(int px = 0, int py = 0) : x(px), y(py) { }
        int x;
        int y;
    };

    int m_chessboard[N][N];     // 棋盘，0表示空位，1表示皇后，2表示边界
    Pos m_direction[3];         // 共3个方向；方向-1、-1表示左斜线；0、-1表示下方；1、-1表示右斜线；首先从最下方开始，所以只需考虑下面的行。
    LinkList<Pos> m_solution;   // 用链表记录解决方案，注意该链表只记录一个方案，而不是全部
    int m_count;                // 记录有效方案数量

    void init()　　　　　　　　　　// 初始化函数
    {
        m_count = 0;                    // 有效方案初始化为0

        for(int i=0; i<N; i+=(N-1))     // 设置棋盘边界，遍历第1行和最后一行
        {
            for(int j=0; j<N; j++)      // 遍历每一列
            {
                m_chessboard[i][j] = 2; // 给棋盘的上下设置边界
                m_chessboard[j][i] = 2; // 给棋盘的左右设置边界
            }
        }

        for(int i=1; i<=SIZE; i++)      // 初始化棋盘为空位，注意0是边界，所以从1开始
        {
            for(int j=1; j<=SIZE; j++)
            {
                m_chessboard[i][j] = 0;
            }
        }

        m_direction[0].x = -1;          // 初始化方向数据
        m_direction[0].y = -1;
        m_direction[1].x = 0;
        m_direction[1].y = -1;
        m_direction[2].x = 1;
        m_direction[2].y = -1;
    }

    void print()                        // 打印有效方案，方案记录了坐标值
    {
        for(m_solution.move(0); !m_solution.end(); m_solution.next())   // 打印坐标
        {
            cout << "(" << m_solution.current().x << ", " << m_solution.current().y << ")" ;
        }

        cout << endl;

        for(int i=0; i<N; i++)          // 打印棋盘
        {
            for(int j=0; j<N; j++)
            {
                switch(m_chessboard[i][j])
                {
                    case 0: cout << " "; break; // 空位
                    case 1: cout << "#"; break; // 皇后
                    case 2: cout << "*"; break; // 边界
                }
            }

            cout << endl;
        }

        cout << endl;                           // 棋盘打印完换行
    }

    bool check(int x, int y, int d)             // 检查是否可放置皇后（xy是假定要放置皇后的坐标，d是要判断有没有皇后的方向值）
    {
        bool flag = true;

        do　　　　　　　　　　　　　　　　　　　　　　 // 查询坐标直至边界或皇后
        {
            x += m_direction[d].x;　　　　　　　　// 坐标向下减少
            y += m_direction[d].y;
            flag = flag && (m_chessboard[x][y] == 0);// 查看坐标位置是否有空位（）
        }
        while( flag );

        return (m_chessboard[x][y] == 2);       // 判断do循环之后的xy值是否到边界，返回真就是到边界可放置皇后，否则就是有皇后不能放置
    }

    void run(int j) // 检查当前行有没有可放置皇后的位置
    {
        if( j <= SIZE ) // 检查当前行在棋盘内，注意不要跑到边界上
        {
            for(int i=1; i<=SIZE; i++)　　　　　　　　　　　　　　　　　　　　　　 // 遍历当前行的所有列
            {
                if( check(i, j, 0) && check(i, j, 1) && check(i, j, 2) )    // 检查当前位置是否可放置皇后，需要判断3个方向
                {
                    m_chessboard[i][j] = 1;                                 // 如果可以放置就标记该处有皇后

                    m_solution.insert(Pos(i, j));                           // 记录皇后的位置到链表

                    run(j + 1);                                             // 递归判断下一行

                    m_chessboard[i][j] = 0;                                 // 返回后要把棋盘当前位置的皇后清除，避免下一次调用时还有上次的皇后位置；

                    m_solution.remove(m_solution.length() - 1);             // 回溯后记录皇后位置的链表长度也要减少，因为之前的方案无效或已经输出；
                }
            }
        }
        else    // 如果j大于SIZE就表示一轮检查结束，方案计数加1并打印方案
        {
            m_count++;

            print();
        }
    }

public:
    QueenSolution()
    {
        init();
    }

    void run()
    {
        run(1); // 从第一行开始，注意边界占用的行数（本例四周都占用了1行或列记录边界，所以从1开始）

        cout << "Total: " << m_count << endl;   // 输出方案个数
    }
};

int main()
{
    QueenSolution<8> qs;

    qs.run();

    return 0;
}

本例来自于狄泰《数据结构》45课第3节整理。