二叉树之红黑树(RBTree)
红黑树(RB-Tree)
引用:https://www.cnblogs.com/skywang12345/
详解以后再补充。。。
红黑树和AVL树6层模式下的最少结点数
通过图可以看到红黑树可以实现更少的结点,反过来说就是同样的结点数红黑树最大数高会超过AVL树
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html这个网站可以测试动态效果,下图就是截图于此
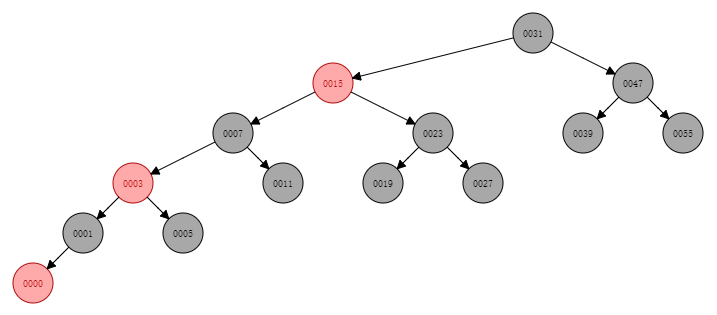

红黑树插入删除步骤

输出
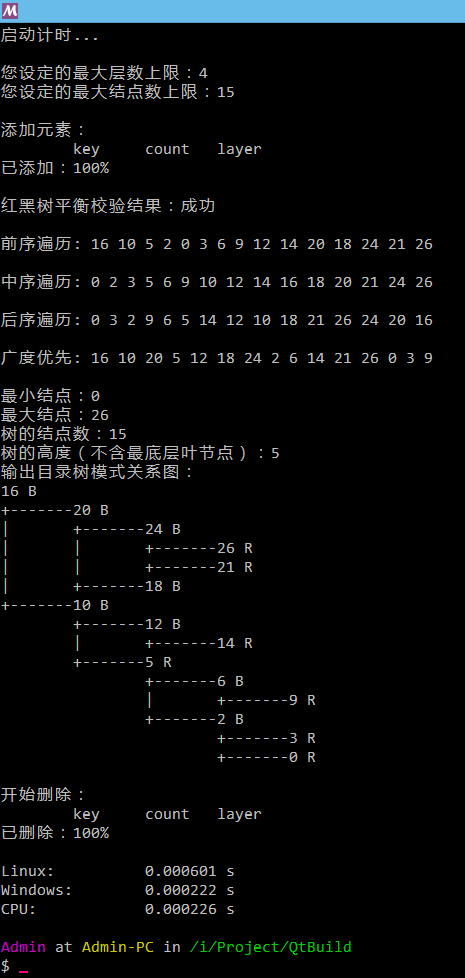
代码
其余代码:https://github.com/Duacai/Data-Structure-and-Algorithms/tree/master/Data-Structure/Tree/RBTree
工程通过Qt Creator创建
RBTree.h
1 #ifndef RBTREE_H 2 #define RBTREE_H 3 4 #include <iostream> 5 #include <iomanip> 6 #include <queue> 7 8 using namespace std; 9 10 namespace Viclib 11 { 12 13 enum RBTColor { RED, BLACK }; 14 15 template <typename T> 16 class RBTNode 17 { 18 public: 19 RBTColor mColor; 20 T mKey; 21 RBTNode<T>* mLeft; 22 RBTNode<T>* mRight; 23 RBTNode<T>* mParent; 24 25 RBTNode(RBTColor color, T key, RBTNode<T>* left, RBTNode<T>* right, RBTNode<T>* parent) : 26 mColor(color), mKey(key), mLeft(left), mRight(right), mParent(parent) {} 27 }; 28 29 template <typename T> 30 class RBTree 31 { 32 private: 33 RBTNode<T>* mRoot; 34 uint64_t mCount; 35 uint16_t mHeight; 36 37 void preOrder(RBTNode<T>* tree) const; 38 void inOrder(RBTNode<T>* tree) const; 39 void postOrder(RBTNode<T>* tree) const; 40 41 void levelOrder(RBTNode<T>* tree) const; 42 43 RBTNode<T>* search(RBTNode<T>* tree, T key) const; 44 RBTNode<T>* iterativeSearch(RBTNode<T>* tree, T key) const; 45 46 RBTNode<T>* minimum(RBTNode<T>* tree) const; 47 RBTNode<T>* maximum(RBTNode<T>* tree) const; 48 49 void lRotate(RBTNode<T>* &tree, RBTNode<T>* node) const; 50 void rRotate(RBTNode<T>* &tree, RBTNode<T>* node) const; 51 52 void insert(RBTNode<T>* &tree, RBTNode<T>* node); 53 void insertFixUp(RBTNode<T>* &tree, RBTNode<T>* node); // 插入修正红黑树 54 55 void remove(RBTNode<T>* &tree, RBTNode<T> *del); 56 void removeFixUp(RBTNode<T>* &tree, RBTNode<T>* del, RBTNode<T>* parent); // 删除修正红黑树(被删除的是黑色) 57 58 void printTree(RBTNode<T> const* const tree, bool firstNode) const; 59 60 void destroy(RBTNode<T>* &tree); 61 uint16_t max(uint16_t left, uint16_t right) const; 62 uint16_t updateHeight(RBTNode<T> *node); 63 64 public: 65 RBTree(); 66 ~RBTree(); 67 68 void preOrder() const; 69 void inOrder() const; 70 void postOrder() const; 71 72 void levelOrder() const; 73 74 RBTNode<T>* search(T key) const; 75 RBTNode<T>* iterativeSearch(T key) const; 76 77 T const* minimum() const; 78 T const* maximum() const; 79 80 RBTNode<T>* successor(RBTNode<T>* node) const; 81 RBTNode<T>* predecessor(RBTNode<T>* node) const; 82 83 void insert(T key); 84 bool remove(T key); 85 86 void printTree() const; 87 88 void destroy(); 89 uint64_t getCount() const; 90 uint16_t getHeight(bool update = true); 91 bool rootIsNullptr() const; 92 T getRootKey() const; 93 uint8_t setKeyStrLen(); 94 }; 95 96 template <typename T> 97 RBTree<T>::RBTree() : mRoot(nullptr), mCount(0ull), mHeight(0) 98 { 99 } 100 101 template <typename T> 102 RBTree<T>::~RBTree() 103 { 104 destroy(); 105 } 106 107 template <typename T> 108 void RBTree<T>::preOrder(RBTNode<T>* tree) const 109 { 110 if ( tree != nullptr ) 111 { 112 cout << tree->mKey << " " << flush; 113 preOrder(tree->mLeft); 114 preOrder(tree->mRight); 115 } 116 } 117 118 template <typename T> 119 void RBTree<T>::preOrder() const 120 { 121 preOrder(mRoot); 122 cout << endl; 123 } 124 125 template <typename T> 126 void RBTree<T>::inOrder(RBTNode<T>* tree) const 127 { 128 if ( tree != nullptr ) 129 { 130 inOrder(tree->mLeft); 131 cout << tree->mKey << " " << flush; 132 inOrder(tree->mRight); 133 } 134 } 135 136 template <typename T> 137 void RBTree<T>::inOrder() const 138 { 139 inOrder(mRoot); 140 cout << endl; 141 } 142 143 template <typename T> 144 void RBTree<T>::postOrder(RBTNode<T>* tree) const 145 { 146 if ( tree != nullptr ) 147 { 148 postOrder(tree->mLeft); 149 postOrder(tree->mRight); 150 cout << tree->mKey << " " << flush; 151 } 152 } 153 154 template <typename T> 155 void RBTree<T>::postOrder() const 156 { 157 postOrder(mRoot); 158 cout << endl; 159 } 160 161 template <typename T> 162 void RBTree<T>::levelOrder(RBTNode<T>* tree) const 163 { 164 if ( tree != nullptr ) 165 { 166 queue<RBTNode<T>*> tmp; 167 tmp.push(tree); 168 169 while( tmp.size() > 0 ) 170 { 171 RBTNode<T>* t = tmp.front(); 172 173 if ( t->mLeft != nullptr ) 174 tmp.push(t->mLeft); 175 176 if ( t->mRight != nullptr ) 177 tmp.push(t->mRight); 178 179 tmp.pop(); 180 181 cout << t->mKey << " " << flush; 182 } 183 } 184 } 185 186 template <typename T> 187 void RBTree<T>::levelOrder() const 188 { 189 levelOrder(mRoot); 190 cout << endl; 191 } 192 193 template <typename T> 194 RBTNode<T>* RBTree<T>::search(RBTNode<T>* tree, T key) const 195 { 196 if ( tree==nullptr || key==tree->mKey ) 197 return tree; 198 199 if ( key < tree->mKey ) 200 return search(tree->mLeft, key); 201 else 202 return search(tree->mRight, key); 203 } 204 205 template <typename T> 206 RBTNode<T>* RBTree<T>::search(T key) const 207 { 208 return search(mRoot, key); 209 } 210 211 template <typename T> 212 RBTNode<T>* RBTree<T>::iterativeSearch(RBTNode<T>* tree, T key) const 213 { 214 while ( tree!=nullptr && key!=tree->mKey ) 215 { 216 if ( key < tree->mKey ) 217 tree = tree->mLeft; 218 else 219 tree = tree->mRight; 220 } 221 222 return tree; 223 } 224 225 template <typename T> 226 RBTNode<T>* RBTree<T>::iterativeSearch(T key) const 227 { 228 return iterativeSearch(mRoot, key); 229 } 230 231 template <typename T> 232 RBTNode<T>* RBTree<T>::minimum(RBTNode<T>* tree) const 233 { 234 if ( tree == nullptr ) 235 return nullptr; 236 237 while ( tree->mLeft != nullptr ) 238 tree = tree->mLeft; 239 240 return tree; 241 } 242 243 template <typename T> 244 T const* RBTree<T>::minimum() const 245 { 246 RBTNode<T>* ret = minimum(mRoot); 247 if ( ret != nullptr ) 248 return &ret->mKey; 249 250 return nullptr; 251 } 252 253 template <typename T> 254 RBTNode<T>* RBTree<T>::maximum(RBTNode<T>* tree) const 255 { 256 if ( tree == nullptr ) 257 return nullptr; 258 259 while ( tree->mRight != nullptr ) 260 tree = tree->mRight; 261 262 return tree; 263 } 264 265 template <typename T> 266 T const* RBTree<T>::maximum() const 267 { 268 RBTNode<T>* ret = maximum(mRoot); 269 if ( ret != nullptr ) 270 return &ret->mKey; 271 272 return nullptr; 273 } 274 275 template <typename T> 276 RBTNode<T>* RBTree<T>::successor(RBTNode<T>* tree) const // 查找tree的后继,比tree大 277 { 278 if ( tree->right != nullptr ) // 在右节点查找最小结点 279 return minimum(tree->right); 280 281 RBTNode<T>* p = tree->parent; 282 while ( p!=nullptr && tree==p->right ) // 父节点非空且自己是右节点就继续寻找,直至自己是左结点或父节点为空 283 { 284 tree = p; 285 p = p->parent; 286 } 287 288 return p; 289 } 290 291 template <typename T> 292 RBTNode<T>* RBTree<T>::predecessor(RBTNode<T>* tree) const // 查找tree的前任,比tree小 293 { 294 if ( tree->left != nullptr ) // 在左结点查找最大结点 295 return maximum(tree->left); 296 297 RBTNode<T>* p = tree->parent; 298 while ( p!=nullptr && tree==p->left ) // 父节点非空且自己是左结点就继续寻找,直至自己是右节点或父节点为空 299 { 300 tree = p; 301 p = p->parent; 302 } 303 304 return p; 305 } 306 307 /* 左旋 308 * p p 309 * | | 310 * old new 311 * / \ --(左旋)--> / \ 312 * a new old c 313 * / \ / \ 314 * B c a B 315 */ 316 template <typename T> 317 void RBTree<T>::lRotate(RBTNode<T>* &tree, RBTNode<T>* node) const // 将右边重的结点旋转至左边重 318 { // 当前结点成为右孩子的左孩子,右孩子的左孩子成为自己的右孩子,右孩子则替换自己位置 319 RBTNode<T>* r = node->mRight; // 新结点指向右节点 320 321 node->mRight = r->mLeft; // 更新 【当前结点(旧结点)】 与 【右节点(新结点)的左孩子】 之间的关系 322 if ( r->mLeft != nullptr ) 323 r->mLeft->mParent = node; 324 325 r->mParent = node->mParent; // 更新 父节点 和 新孩子 之间的关系 326 if ( node->mParent == nullptr ) 327 tree = r; 328 else 329 { 330 if ( node == node->mParent->mLeft ) // 判断并更新父节点的新孩子 331 node->mParent->mLeft = r; 332 else 333 node->mParent->mRight = r; 334 } 335 336 r->mLeft = node; // 更新 新旧结点 之间的关系 337 node->mParent = r; 338 } 339 340 /* 右旋 341 * p p 342 * | | 343 * old new 344 * / \ --(右旋)--> / \ 345 * new c a old 346 * / \ / \ 347 * a B B c 348 */ 349 template <typename T> 350 void RBTree<T>::rRotate(RBTNode<T>* &tree, RBTNode<T>* node) const 351 { 352 RBTNode<T>* l = node->mLeft; 353 354 node->mLeft = l->mRight; 355 if ( l->mRight != nullptr ) 356 l->mRight->mParent = node; 357 358 l->mParent = node->mParent; 359 if ( node->mParent == nullptr ) 360 tree = l; 361 else 362 { 363 if ( node == node->mParent->mLeft ) 364 node->mParent->mLeft = l; 365 else 366 node->mParent->mRight = l; 367 } 368 369 l->mRight = node; 370 node->mParent = l; 371 } 372 373 template <typename T> 374 void RBTree<T>::insertFixUp(RBTNode<T>* &tree, RBTNode<T>* node) // 插入修正红黑树 375 { 376 RBTNode<T> *parent, *gparent; // 父结点,爷爷结点 377 378 // node有父结点且父亲是红色(R红色、B黑色、@插入结点) 379 while ( (parent = node->mParent) && (parent->mColor==RED) ) 380 { 381 gparent = parent->mParent; 382 383 if ( parent == gparent->mLeft ) // 父亲是左孩子,叔叔是右孩子 384 { 385 { // 叔叔有效且是红色,while保证父亲也是红色 386 RBTNode<T>* uncle = gparent->mRight; 387 if ( uncle && uncle->mColor==RED ) // 父亲是红色,自己默认又是红色,所以需要变色 388 { // 将父亲和叔叔设为黑结点,爷爷设为红节点; 389 uncle->mColor = BLACK; // B R 390 parent->mColor = BLACK; // R R B B 391 gparent->mColor = RED; // R(@) R(@) // 不区分自己是左孩子还是右孩子 392 node = gparent; // node指向爷爷后向上再判断其它结点是否需要平衡 393 continue; 394 } 395 } 396 // 父亲为红色时如果叔叔不是红色,则叔叔必是黑色叶子,且父亲的子女也全是叶子;因为父亲必须有一个叶子子结点才能插入,如果叔叔不是叶子或父亲的儿子不全是叶子则无法平衡 397 { // 叔叔为空,自己是红色父亲的右孩子,旋转成左孩子(父子身份也交换,且父子仍为红色) 398 if ( parent->mRight == node )// 红节点的子结点如有叶子则全是叶子,否则不平衡;父亲之前没有子结点则父亲无兄弟 399 { 400 RBTNode<T>* tmp; 401 lRotate(tree, parent); // 左旋后node替换父亲,父亲则成为自己的左孩子,变成左左模式,左左都是红色 402 tmp = parent; // 旋转后修正父子指针位置,父子互换 403 parent = node; // B B B 404 node = tmp; // R R(@) R 405 } // R(@) R R(@) 406 } 407 408 { // 叔叔为空,自己是红色父亲的左孩子 409 parent->mColor = BLACK; // B R B 410 gparent->mColor = RED; // R B R(@) R 411 rRotate(tree, gparent); // R(@) R(@) 412 } 413 } 414 else // 父亲是右孩子,伯父是左孩子 415 { 416 { // 伯父有效且是红色,while保证父亲也是红色 417 RBTNode<T>* uncle = gparent->mLeft; 418 if ( uncle && uncle->mColor==RED ) 419 { 420 uncle->mColor = BLACK; // B R 421 parent->mColor = BLACK; // R R B B 422 gparent->mColor = RED; // R(@) R(@) 423 node = gparent; 424 continue; 425 } 426 } 427 428 { // 伯父为空或为黑色,自己是红色父亲的左孩子,旋转成右孩子(父子身份也交换,且父子仍为红色) 429 if ( parent->mLeft == node ) 430 { 431 RBTNode<T>* tmp; 432 rRotate(tree, parent); 433 tmp = parent; // B B B 434 parent = node; // R R(@) R 435 node = tmp; // R(@) R R(@) 436 } 437 } 438 439 { // 伯父为空或为黑色,自己是红色父亲的右孩子 440 parent->mColor = BLACK; // B R B 441 gparent->mColor = RED; // R # R R(@) 442 lRotate(tree, gparent); // R(@) R(@) 443 } 444 } 445 } 446 447 tree->mColor = BLACK; // 如果没有父节点则当前结点就是根节点;父节点为黑则这条语句无意义 448 } 449 450 template <typename T> 451 void RBTree<T>::insert(RBTNode<T>* &tree, RBTNode<T>* node) 452 { 453 RBTNode<T>* parent = nullptr; // 插入点的父节点 454 RBTNode<T>* root = tree; // 辅助寻找parent 455 456 while ( root != nullptr ) // 寻找插入点 457 { 458 parent = root; 459 if ( node->mKey < root->mKey ) 460 root = root->mLeft; 461 else 462 root = root->mRight; 463 } 464 465 node->mParent = parent; // 设置node结点的父节点 466 if ( parent != nullptr ) // 有父节点则插入为子结点 467 if ( node->mKey < parent->mKey ) 468 parent->mLeft = node; 469 else 470 parent->mRight = node; 471 else // 父节点为空则设为根节点 472 tree = node; 473 474 node->mColor = RED; // 设为红色 475 ++mCount; 476 477 insertFixUp(tree, node); // 只有父节点是红色才需要平衡,但是要注意根节点没有父亲且默认插入的是红色 478 } 479 480 template <typename T> 481 void RBTree<T>::insert(T key) 482 { 483 RBTNode<T>* node = new RBTNode<T>(RED, key, nullptr, nullptr, nullptr); // 颜色在重载版本改为红色,此处可任意填写 484 485 insert(mRoot, node); 486 } 487 488 template <typename T> 489 void RBTree<T>::removeFixUp(RBTNode<T>* &tree, RBTNode<T>* del_child, RBTNode<T>* del_parent) // 删除修正红黑树(被删除的是黑色) 490 { 491 RBTNode<T>* other; // child的兄弟(原来的叔伯) 492 493 // del_child为假或del_child为黑结点,且del_child不是根节点(del_child如果不是根节点就绝对是nullptr) 494 while ( (!del_child || del_child->mColor==BLACK) && del_child!=tree ) // B黑,R红,p=parent,c=child,o=other,ol=other->left,or=other->right 495 { 496 if ( del_parent->mLeft == del_child ) // 如果del_child是左结点;注意替换者已经离开了,所以child和parent是父子关系 497 { // 父亲绝对有两个儿子,因为del_child原先是黑色孙子,所以绝对有一个叔伯(现在是兄弟) 498 other = del_parent->mRight; 499 if ( other->mColor == RED ) // del_child的兄弟是红节点,它的子结点必定全是黑色 500 { 501 other->mColor = BLACK; 502 del_parent->mColor = RED; 503 lRotate(tree, del_parent); 504 other = del_parent->mRight; 505 } 506 507 if ( (!other->mLeft || other->mLeft->mColor==BLACK) && // del_child兄弟的左结点为假或者为黑,且右结点也为假或者为黑 508 (!other->mRight || other->mRight->mColor==BLACK) ) // 上面if保证del_child的兄弟也是黑色 509 { 510 other->mColor = RED; 511 del_child = del_parent; 512 del_parent = del_child->mParent; 513 } 514 else 515 { 516 if ( !other->mRight || other->mRight->mColor==BLACK ) // del_child兄弟是黑色,且该兄弟孩子不全为黑 517 { 518 other->mLeft->mColor = BLACK; 519 other->mColor = RED; 520 rRotate(tree, other); 521 other = del_parent->mRight; 522 } 523 524 other->mColor = del_parent->mColor; 525 del_parent->mColor = BLACK; 526 other->mRight->mColor = BLACK; 527 lRotate(tree, del_parent); 528 del_child = tree; 529 break; 530 } 531 } 532 else // 如果del_child是右结点 533 { 534 other = del_parent->mLeft; 535 if ( other->mColor == RED ) 536 { 537 other->mColor = BLACK; 538 del_parent->mColor = RED; 539 rRotate(tree, del_parent); 540 other = del_parent->mLeft; 541 } 542 543 if ( (!other->mLeft || other->mLeft->mColor==BLACK) && 544 (!other->mRight || other->mRight->mColor==BLACK) ) 545 { 546 other->mColor = RED; 547 del_child = del_parent; 548 del_parent = del_child->mParent; 549 } 550 else 551 { 552 if ( !other->mLeft || other->mLeft->mColor==BLACK ) 553 { 554 other->mRight->mColor = BLACK; 555 other->mColor = RED; 556 lRotate(tree, other); 557 other = del_parent->mLeft; 558 } 559 560 other->mColor = del_parent->mColor; 561 del_parent->mColor = BLACK; 562 other->mLeft->mColor = BLACK; 563 rRotate(tree, del_parent); 564 del_child = tree; // 也可以改成 tree->color = BLACK; 565 break; 566 } 567 } 568 } 569 570 if ( del_child != nullptr ) // del_child如果存在且是红色,或者是根节点 571 del_child->mColor = BLACK; 572 } 573 574 template <typename T> 575 void RBTree<T>::remove(RBTNode<T>* &tree, RBTNode<T>* del) 576 { 577 RBTNode<T> *child, *parent; 578 RBTColor color; 579 580 if ( del->mLeft!=nullptr && del->mRight!=nullptr ) // 如果删除结点有两个孩子,需要找一个替换者 581 { 582 RBTNode<T>* replace = del->mRight; // 替换者指向右结点最小者;也可以指向左结点的最大者 583 while ( replace->mLeft != nullptr ) 584 replace = replace->mLeft; 585 586 if ( del->mParent != nullptr ) // 更新父结点指向替换者 587 { 588 if ( del->mParent->mLeft == del ) 589 del->mParent->mLeft = replace; 590 else 591 del->mParent->mRight = replace; 592 } 593 else 594 tree = replace; 595 596 child = replace->mRight; // 保存替换者的子结点、父结点、颜色 597 parent = replace->mParent; 598 color = replace->mColor; 599 600 if ( del == parent ) // 删除的是替换者的父结点(这时替换者就是del的右结点,因为替换者没有左结点,所以del的右结点最小) 601 parent = replace; 602 else 603 { 604 if ( child != nullptr ) 605 child->mParent = parent; 606 parent->mLeft = child; // 替换者的父亲接管替换者的儿子(此时替换者只有右儿子,因为自己是右子树的最左下者) 607 608 replace->mRight = del->mRight; // 更新替换者和被删除者右儿子的关系(因为替换者位于右子树) 609 del->mRight->mParent = replace; 610 } 611 612 replace->mParent = del->mParent; // 更新替换者的父亲、颜色、以及与被删除者左结点的关系 613 replace->mColor = del->mColor; 614 replace->mLeft = del->mLeft; 615 del->mLeft->mParent = replace; 616 } 617 else // 删除结点孩子不足两个,独子或者叶节点就是替换者 618 { 619 if ( del->mLeft != nullptr ) // 保存替换者的子结点、父结点、颜色 620 child = del->mLeft; 621 else 622 child = del->mRight; 623 parent = del->mParent; 624 color = del->mColor; 625 626 if ( child != nullptr ) // 更新 '被删除结点的父节点' 和 '被删除结点的子结点' 的关系 627 child->mParent = parent; // 父亲(也就是被删除结点)被删除,所以爷爷直接和唯一一个孙子互相更新关系即可 628 if ( parent != nullptr ) 629 { 630 if ( parent->mLeft == del ) 631 parent->mLeft = child; 632 else 633 parent->mRight = child; 634 } 635 else 636 tree = child; 637 } 638 639 --mCount; // 结点计数减一 640 641 if ( color == BLACK ) // 如果替换者或被删除者是黑色需要重新平衡(被删除者有两个儿子则是替换者),因为删除了一个黑结点 642 removeFixUp(tree, child, parent); // child如果不是根节点或红色节点,那它绝对是nullptr指针(替换者至多有一个红色儿子,且该儿子没有后代) 643 644 delete del; // 删除节点并返回 645 del = nullptr; 646 } 647 648 template <typename T> 649 bool RBTree<T>::remove(T key) 650 { 651 bool ret = false; 652 RBTNode<T>* node = search(mRoot, key); 653 654 if ( node != nullptr ) 655 { 656 remove(mRoot, node); 657 ret = true; 658 } 659 660 return ret; 661 } 662 663 template <typename T> 664 void RBTree<T>::printTree(RBTNode<T> const* const tree, bool firstNode) const 665 { 666 if ( tree==nullptr ) 667 return; 668 669 bool static outTag[64] = {false}; // size = max layer limit; 670 uint8_t static layer = 0; 671 uint8_t i; 672 ++layer; 673 674 if ( layer >= 2 ) 675 { 676 for (i=2; i<layer; ++i ) 677 if ( outTag[i] ) 678 cout << "| "; 679 else 680 cout << " "; 681 cout << "+-------" << flush; 682 } 683 cout << tree->mKey << ' ' << (tree->mColor==BLACK ? 'B' : 'R') << endl; 684 685 for ( i=2-1; i>0; --i) // 从右往左输出结点,即先打印最右边结点,其次次右边的结点;此循环不输出最左边的结点 686 { 687 if ( (tree->mLeft+i) != nullptr ) // 注意树的子结点指针必须是从左往右依次排列,中间不能有其它变量(left_1,left_2,left_3...left_n) 688 { // 如果你的子结点数量不定,一定要把后面的首个指针设为nullptr 689 outTag[layer] = !firstNode; 690 printTree(tree->mRight, false); 691 } 692 } 693 if ( tree->mLeft != nullptr ) // 输出最左边的结点 694 { 695 printTree(tree->mLeft, true); 696 outTag[layer] = firstNode; 697 } 698 699 --layer; 700 } 701 702 template <typename T> 703 void RBTree<T>::printTree() const 704 { 705 printTree(mRoot, true); // 右边参数此时无意义 706 } 707 708 template <typename T> 709 void RBTree<T>::destroy(RBTNode<T>* &tree) 710 { 711 if ( tree == nullptr ) 712 return; 713 714 if ( tree->mLeft != nullptr ) 715 destroy(tree->mLeft); 716 if ( tree->mRight != nullptr ) 717 destroy(tree->mRight); 718 719 delete tree; 720 } 721 722 template <typename T> 723 void RBTree<T>::destroy() 724 { 725 destroy(mRoot); 726 727 mRoot = nullptr; 728 mCount = 0ull; 729 mHeight = 0; 730 } 731 732 template <typename T> 733 uint64_t RBTree<T>::getCount() const 734 { 735 return mCount; 736 } 737 738 template <typename T> 739 uint16_t RBTree<T>::updateHeight(RBTNode<T> *node) 740 { 741 if ( node == nullptr ) 742 return 0; 743 744 return max(updateHeight(node->mLeft), updateHeight(node->mRight))+1; 745 } 746 747 template <typename T> 748 uint16_t RBTree<T>::getHeight(bool update) 749 { 750 if ( update == true ) 751 mHeight = updateHeight(mRoot); 752 753 return mHeight; 754 } 755 756 template <typename T> 757 uint16_t RBTree<T>::max(uint16_t left, uint16_t right) const 758 { 759 return (left > right) ? left : right; 760 } 761 762 template <typename T> 763 bool RBTree<T>::rootIsNullptr() const 764 { 765 return mRoot==nullptr; 766 } 767 768 template <typename T> 769 T RBTree<T>::getRootKey() const 770 { 771 return (rootIsNullptr()) ? ~0ull : mRoot->mKey; 772 } 773 774 } 775 776 #endif // RBTREE_H
main.cpp
1 #include "RBTree.h" 2 3 #include "Times.h" 4 5 using namespace std; 6 using namespace Viclib; 7 8 typedef uint64_t templateType; 9 typedef uint64_t sizeType; 10 11 static bool checkTree(RBTree<templateType>* tree); 12 13 int main(int argc, char* argv[]) 14 { 15 // msys2终端1920*2宽424个英文字符 16 uint16_t layer = 16; 17 18 if ( argc == 2 && atoi(argv[1])>=0 ) 19 layer = static_cast<uint16_t>(atoi(argv[1])); 20 else { 21 cout << "请输入结点层数,注意内存大小" << endl; 22 cin >> layer; 23 } 24 25 timingStart(); 26 cout << endl; 27 28 uint64_t const count = (1ull<<layer)-1ull; 29 30 cout << "您设定的最大层数上限:" << layer << endl; 31 cout << "您设定的最大结点数上限:" << count << endl; 32 33 templateType *t = nullptr, tmp = 0; 34 RBTree<templateType>* tree = new RBTree<templateType>(); 35 36 cout << endl << "添加元素:\n\tkey\tcount\tlayer" << endl; 37 srand(static_cast<uint32_t>(time(nullptr))); 38 while ( tree->getCount() < count ) 39 { 40 do 41 { 42 tmp = static_cast<templateType>( 43 static_cast<sizeType>(rand()) 44 * static_cast<sizeType>(rand()) 45 * static_cast<sizeType>(rand()) 46 % (count*2)); 47 } while(tree->iterativeSearch(tmp)); 48 //tmp = setArr(count); 49 tree->insert(tmp); 50 //cout << "插入:\t" << tmp << "\t" << tree->getCount() << "\t" << tree->getHeight(true) << endl; 51 52 if ( (tree->getCount()*100%count) == 0 || tree->getCount() == count ) 53 cout << "\r已添加:" << setw(2) << tree->getCount()*100.0/count << '%' << flush; 54 } 55 cout << endl; 56 57 cout << "\n红黑树平衡校验结果:"; 58 if ( checkTree(tree) ) 59 cout << "成功\n" << endl; 60 else 61 { 62 cout << "节点的路径与左边第一个节点路径黑色数量不同\n" << endl; 63 64 cout << "输出目录树模式关系图:" << endl; 65 tree->printTree(); 66 cout << endl; 67 68 exit(1); 69 } 70 71 cout << "前序遍历: "; 72 tree->preOrder(); 73 cout << "\n中序遍历: "; 74 tree->inOrder(); 75 cout << "\n后序遍历: "; 76 tree->postOrder(); 77 cout << "\n广度优先: "; 78 tree->levelOrder(); 79 cout << endl; 80 81 if ( (tree!=nullptr) && ((t = const_cast<templateType*>(tree->minimum())) != nullptr) ) 82 cout << "最小结点:" << *t << endl; 83 if ( (tree!=nullptr) && ((t = const_cast<templateType*>(tree->maximum())) != nullptr) ) 84 cout << "最大结点:" << *t << endl; 85 cout << "树的结点数:" << tree->getCount() << endl; 86 cout << "树的高度(不含最底层叶节点):" << tree->getHeight(true) << endl; 87 88 // cout << "输出树形关系图:" << endl; 89 // tree->printGraph(); 90 // cout << endl; 91 92 cout << "输出目录树模式关系图:" << endl; 93 tree->printTree(); 94 cout << endl; 95 96 cout << "开始删除:\n\tkey\tcount\tlayer" << endl; 97 srand(static_cast<uint32_t>(time(nullptr))); 98 while ( !tree->rootIsNullptr() ) // 随机数删除 99 { 100 do 101 { 102 tmp = static_cast<templateType>( 103 static_cast<sizeType>(rand()) 104 * static_cast<sizeType>(rand()) 105 * static_cast<sizeType>(rand()) 106 % (count*2)); 107 } while(!tree->iterativeSearch(tmp)); 108 if ( tree->remove(tree->getRootKey()) ) 109 { 110 //cout << "删除:\t" << tmp << "\t" << tree->getCount() << "\t" << tree->getHeight(true) << endl; 111 112 if ( (tree->getCount()*100%count) == 0 || tree->getCount() == count ) 113 cout << "\r已删除:" << setw(2) << (count-tree->getCount())*100.0/count << '%' << flush; 114 } 115 } 116 cout << endl; 117 118 tree->destroy(); 119 tree = nullptr; 120 121 cout << endl; 122 timingEnd(); 123 124 return 0; 125 } 126 127 static bool checkTree(RBTree<templateType>* tree) 128 { 129 if ( tree == nullptr ) 130 return true; 131 132 queue<RBTNode<templateType>*> tmp; 133 tmp.push(tree->search(tree->getRootKey())); 134 queue<RBTNode<templateType>*> leaf; 135 RBTNode<templateType>* t; 136 uint8_t i = 0; 137 uint8_t j = 0; 138 139 while( tmp.size() > 0 ) 140 { 141 t = tmp.front(); 142 143 if ( t->mLeft != nullptr ) 144 tmp.push(t->mLeft); 145 else 146 leaf.push(t); 147 148 if ( t->mRight != nullptr ) 149 tmp.push(t->mRight); 150 else 151 leaf.push(t); 152 153 tmp.pop(); 154 } 155 156 t = leaf.front(); 157 leaf.pop(); 158 while ( t != nullptr ) 159 { 160 if ( t->mColor == BLACK ) ++i; 161 t = t->mParent; 162 } 163 164 while ( !leaf.empty() ) 165 { 166 t = leaf.front(); 167 168 j = 0; 169 if ( t->mColor == BLACK ) ++j; 170 while ( t->mParent != nullptr ) 171 { 172 t = t->mParent; 173 if ( t->mColor == BLACK ) ++j; 174 } 175 176 if ( i != j ) 177 { 178 cout << leaf.front()->mKey; 179 return false; 180 } 181 182 leaf.pop(); 183 } 184 185 return true; 186 }


