最小路径和

题目描述：

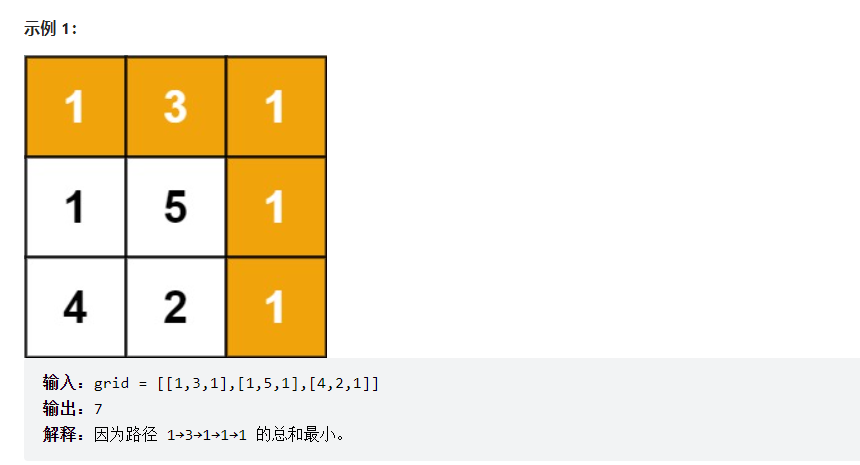
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

 

 

 

 

    
    /**
     * 解题思路：
     *      第一步：确定dp数组，本题定义一个二维dp数组，那么dp[i][j]表示为在(i,j)位置，由(0,0) --> (i,j)最短路径
     *      第二步：确定递推公式，根据题意可知，dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1]) + grid[i][j]
     *      第三步：初始化。我们一般都是初始化第一行和第一列，那么dp[0][i] = grid[0][i] + dp[0][i-1],dp[j][0] = dp[j - 1][0] + grid[j][0]
     *      如果想不明白，那么你可以这样想，输入的数组是一个1 * n或者 n * 1，我想这样你就会明白初始化
     *      第四步：遍历顺序，就是正常遍历
     *      第五步：返回右下角即可
     * @param grid
     * @return
     */
    public static int minPathSum(int[][] grid) {
        int a = grid.length;
        int b = grid[0].length;
        int[][] arr = new int[a][b];
        int tmp = 0;
        for(int i = 0;i < b;i++){
            arr[0][i] = grid[0][i] + tmp;
            tmp = arr[0][i];
        }
        tmp = 0;
        for(int i = 0;i < a;i++){
            arr[i][0] = grid[i][0] + tmp;
            tmp = arr[i][0];
        }
        for(int i = 1;i < a;i++){
            for(int j = 1;j < b;j++){
                arr[i][j] = Math.min(arr[i][j-1],arr[i-1][j]) + grid[i][j];
            }
        }
        return arr[a-1][b-1];
    }