快速幂
首先我们来补充
模意义下运算的一些基本知识
1.定义: 设a=kb+r 则a mod b=r (0<=r<b)
或写作a≡r(mod b)——>数学上的写法 或 a%b=r 均等价
r=a-kb(被除数-除数*商)
例子(1) 5%3=2 5/3=1...2;
(2)-5%3=?(较坑)
解: 根据定义 先算出除数
那么-5/3=-1
由r=a-kb得 r=-5-3*(-1)=-2;
(3)-5%(-3)=?
解(-5)/(-3)=1; 由r=a-kb得 r=-5-(-3)*1=-2
注意:正%正=正 负%正=负 负%负=负
总结:换种说法来说,在摸运算中,决定你答案的符号(即余数的符号),只和“%”符号前那个数有关
取模后答案的符号与“%”符号前面的数的符号有关。
- 模运算的性质
(模运算的优先级与乘法与除法是一样的)
性质一(a+b)mod p=(a mod p + b mod p) mod p
性质二(a*b)mod p=(a mod p)*(b mod p) mod p
由性质一可得 我们在做运算时可以边加边模
例如 给n个数 a1,a2,a3,...,an 要把这n个数加起来再摸p(即计算(a1+a2+a3+...+an)%p)
注意:如果先把n个数加起来的话,可能会出现爆int的情况
所以我们的做法可以是 先立一个ans=0,然后for i=1 to n(伪代码),我们就可以让ans=(ans+ai)%p
注意:因为第一条性质说,你在做加法运算的时候,中间任意多次的模p,对结果不产生影响。
例:(a+b)mod p也与[a+(b mod p)mod p]是相等的
也就是说,你中间可以做任意多次的模p或不模p,对结果不产生影响。
所以说在做类似的多个数值求和再取模的问题时,可以把ans随时加上一个数再随时模p,这样的运算,我们就把它叫做边加边模。
同理,这种运算在加法,减法以及乘法都是成立的。
即算乘积时亦可用此方法 令ans=1;for 1 to n;ans=(ans*ai)%p;
总结:在做类似题目时,无论是加法,减法,乘法,要边取模边做运算,以防止运算的过程中爆掉int(重要)
小问题:思考如何证明第二条性质
令a=a1p+r1 ; b=b1p+r2
此时a%p=r1;b%p=r2;
(a*b)%p=(a1b1p + a1r2p + b1r1p + r1r2)%p
因为前面三项均为p的倍数 所以最后的结果等于r1r2 % p
同理如果算的为(a%p)*(b%p)%p的话,结果依旧为r1r 2% p
故性质二成立 证毕
下面进入正题
快速幂(目标 给定x,y,p,计算x^y mod p(x,y,p均为小于10^9的整数))
初步思考可以写出一个伪代码: ans=1;
for i=1 to y; ans=(ans * x)%p
解释一下这段代码 根据所求,我们就先暴力枚举下来然后边乘边模。
找一找问题:
第一点,在ans=(ans * x)%p中,虽然整个过程中都对p取了模,说明了ans是一个小于10^9的数的,
由题意可知 x也是小于10^9的数,所以ans * x会变为一个小于10^18的数,众所周知,int的范围是在(-2)^31到(2^31)-1的,2^31大概在2*10^9左右,所以一乘,ans * x在取模之前是要爆int 的
下面介绍两种解决方法:
- 声明变量时,把所有int的类型开成long long(不推荐,较慢)
- 在ans * x处做一个强制类型转换(3种方法)
方法1:(long long)ans * x % p;
方法2: 1ll * ans * x % p;
1ll代表一个long long类型的1
平常在c++中写一个1其实是一个int类型的1,如果在后面加一个ll的话,它就变成了一个long long类型的1
方法3:同理,也可以写作(0ll+ans)% p;
一个long long类型加上一个int类型,结果应为long long
那为什么不把ans直接开成long long呢
因为两个long long相乘要稍慢于一个long long乘以一个int的,故不推荐直接把ans开成long long
第二点,这段代码的复杂度显然是O(y)的,看一下我们的数据范围,x,y,p均小于等于10^9;
因此在最坏情况下,这个代码运行完成需要10^9次
现在的计算机一秒钟运算的次数大约为 3*10^8到8*10^8这个量级
因此如果设计一个程序想要它 1s跑出来的话,大约是需要保证运算次数小于等于10^8次(因为计算复杂度时没有计算常数,所以需要给常数预留一定的空间)
所以就需要程序跑得更快
那怎么做呢
不妨想一想,O(y)的复杂度核心来自我们暴力枚举x^y,使y个x相乘做了x-1个乘法运算
那换句话说,我们想要让这个算法变快,我们就要设法使做乘法的次数更少,便可以让复杂度变得更少
比如 x^37我们可以写成(x^18)^2 * x,如果我们知道x^18的值,那么我们仅需要两次乘法便可以求出结果,所以问题就变成了如何求x^18,我们又可以用类似方法,将x^18表示为(x^9)^2
过程如下
x^37-->(x^18)^2 * x
x^18-->(x^9)^2
x^9-->(x^4)^2 * x
x^4-->(x^2)^2
x^2-->x * x 总共需要7次乘法,即可算出x^37
这种方法就叫做快速幂,它通过一种折半的思想,不断把更大的问题换成更小的问题的组合
最后附上代码
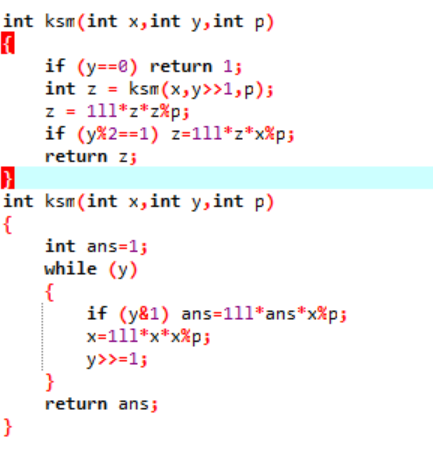
第一次写博客,还请各位大佬提出自己宝贵的意见(深深感谢)!!!


