数据结构与算法(四):树和二叉树
什么是二叉树?
树的定义
树(tree)是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
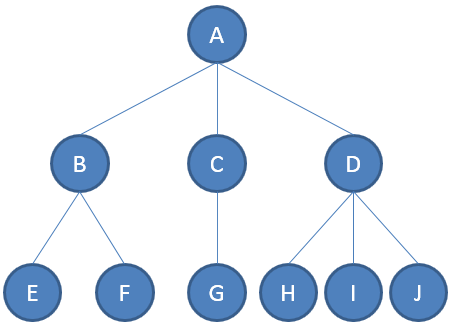
树的相关概念
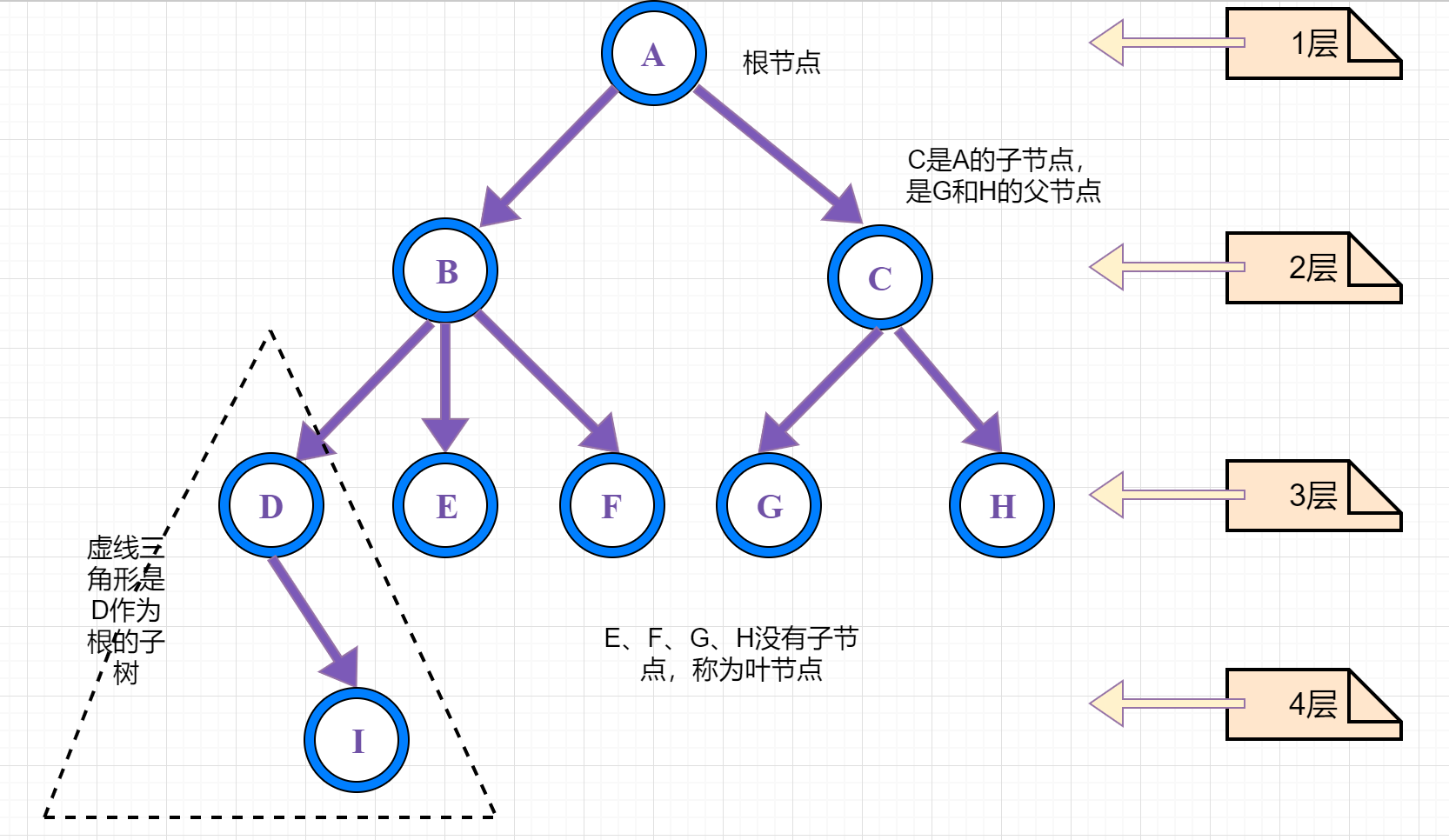
①、路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”。
②、根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
③、父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
④、子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
⑤、兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
⑥、叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的A、E、F、G都是叶子节点。
⑦、子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
⑧、节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
⑨、深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
⑩、高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
二叉树的定义
如果了解了什么是树,那在这里二叉树也很好理解了。二叉树最基础的树类型结构,掌握二叉树的中序、前序、后序遍历方式,二叉树的插入和删除操作,为学习更复杂的二叉树打下扎实的基础
二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
与普通树不同,普通树的节点个数至少为1,而二叉树的节点个数可以为0;普通树节点的最大分支度没有限制,而二叉树节点的最大分支度为2;普通树的节点无左、右次序之分,而二叉树的节点有左、右次序之分。
二叉树的特殊类型
二叉树有两种特殊类型 满二叉树 和 完全二叉树
满二叉树
满二叉树比较好理解,即一棵深度为k,且有
如下图所示:
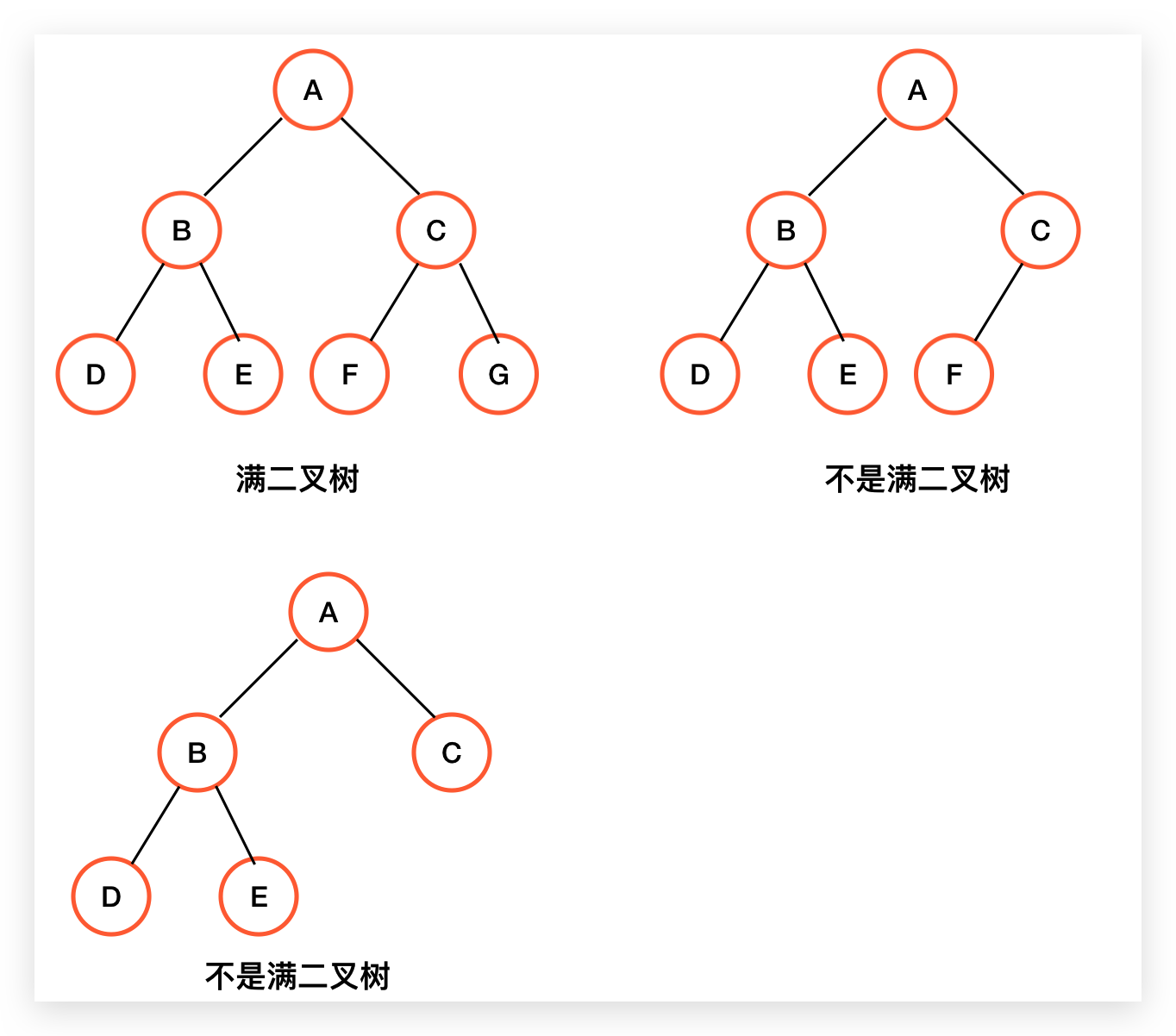
满二叉树是是平衡的,左右对称,具备以下特点:
1、所有叶子节点都在同一层。
2、非叶子节点的度一定是 2 (节点的度表示该节点的子树个数)。
3、同样深度的二叉树中,满二叉树的叶子节点最多。
完全二叉树
从概念上来讲,完全二叉树是指,如果对一棵有 n 个节点的二叉树按层次编号(从上到下,从左到右),如果任意编号 i 的节点与同样深度的满二叉树中编号为 i 的节点位置完全相同,则这棵树为完全二叉树。配合下图,可以更好的理解概念:
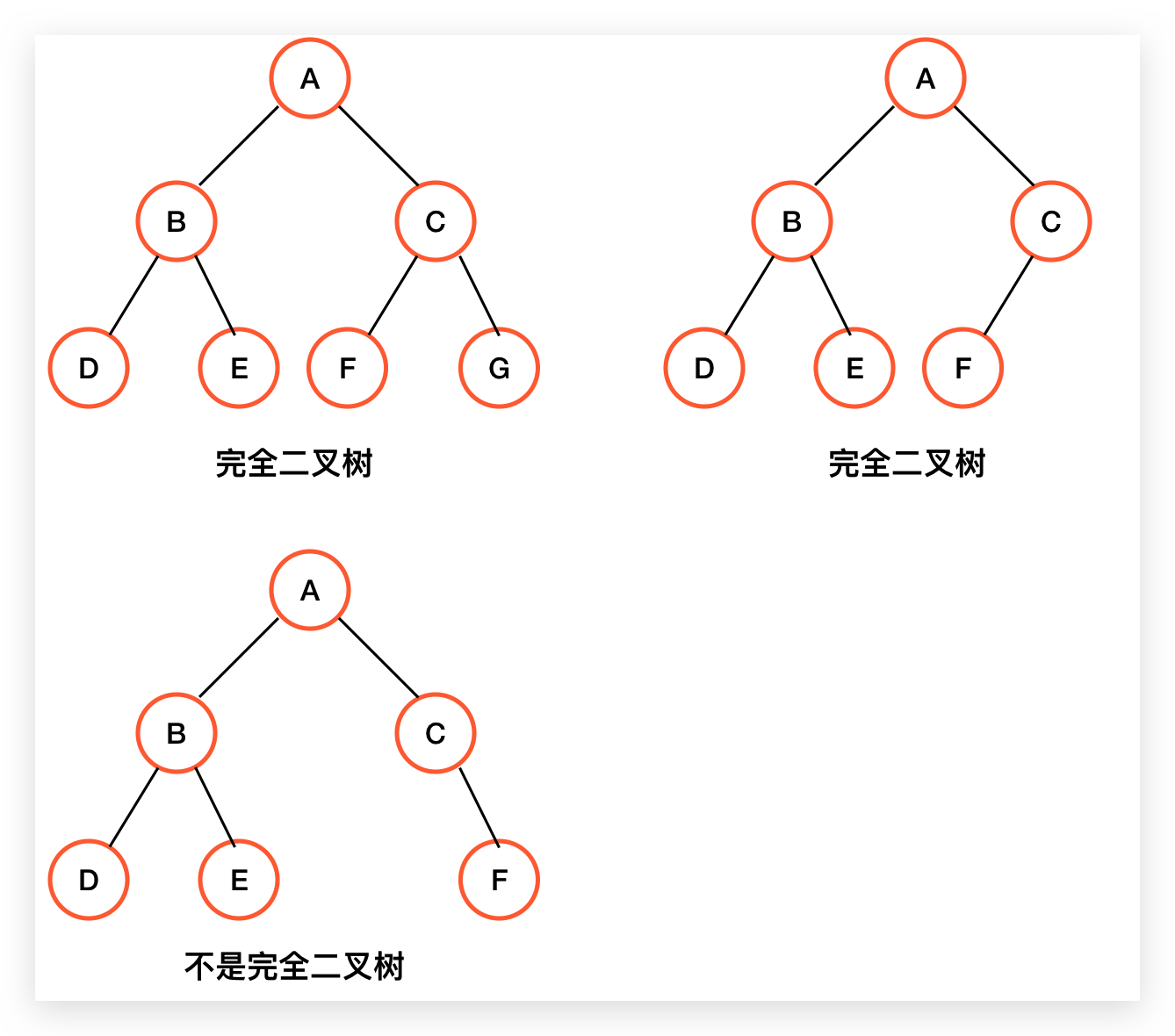
所以满二叉树一定是完全二叉树,反过来则不一定是,完全二叉树具备以下特点:
1、叶子节点只能出现在最下两层
2、如果节点的度为 1,则该节点只能有左子树,不存在只有右子树的情况。
完全二叉树用数组表示

二叉树的遍历
二叉树的遍历分为深度优先遍历(简称:DFS)和 广度优先遍历 (简称:BFS),其中 中序、前序、后序 三种遍历方式属于深度优先遍历,广度优先遍历需要借助队列按层遍历每个节点。
深度优先遍历(DFS)
二叉树的 中序遍历、前序遍历、后序遍历 都属于深度优先遍历。前中后说的是根节点的顺序,前序访问顺序:根 -> 左 -> 右;中序访问顺序:左 -> 根 -> 右;后序访问顺序:左 -> 右 -> 根;
举个栗子:
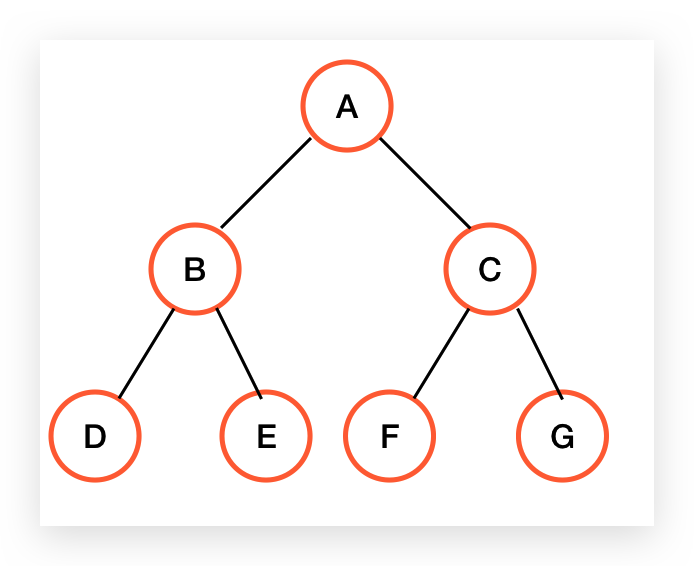
针对上边二叉树
前序遍历:A B D E C F G
中序遍历:D B E A F C G
后序遍历:D E B F G C A
下面是深度优先遍历相关代码:
public class PrintTree {
public static void main(String[] args) {
BinaryTreeNode<String> root = new BinaryTreeNode("A");
root.left = new BinaryTreeNode("B");
root.right = new BinaryTreeNode("C");
root.left.left = new BinaryTreeNode("D");
root.left.right = new BinaryTreeNode("E");
root.right.left = new BinaryTreeNode("F");
root.right.right = new BinaryTreeNode("G");
PrintTree printTree = new PrintTree();
printTree.preOrderTree(root);
System.out.println("前序遍历");
printTree.inOrderTree(root);
System.out.println("中序遍历");
printTree.postOrderTree(root);
System.out.println("后序遍历");
}
/**
* 前序遍历:根 -> 左 -> 右
*
* @param root
*/
public void preOrderTree(BinaryTreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " ");
preOrderTree(root.left);
preOrderTree(root.right);
}
/**
* 中序遍历:左 -> 根 -> 右
*
* @param root
*/
public void inOrderTree(BinaryTreeNode root) {
if (root == null) {
return;
}
preOrderTree(root.left);
System.out.print(root.val + " ");
preOrderTree(root.right);
}
/**
* 后序遍历:左 -> 右 -> 根
*
* @param root
*/
public void postOrderTree(BinaryTreeNode root) {
if (root == null) {
return;
}
preOrderTree(root.left);
preOrderTree(root.right);
System.out.print(root.val + " ");
}
private static class BinaryTreeNode<T> {
public T val;
public BinaryTreeNode left;
public BinaryTreeNode right;
public BinaryTreeNode() {
}
public BinaryTreeNode(T value) {
this.val = value;
}
public BinaryTreeNode(T val, BinaryTreeNode left, BinaryTreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
广度优先遍历(BFS)
广度优先遍历从根节点开始借助队列,一层层的遍历二叉树。
如下图所示:
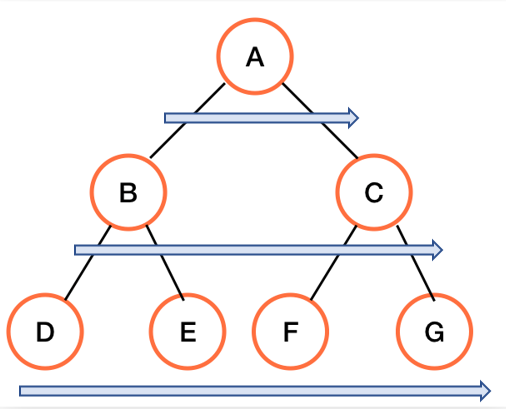
广度优先遍历结果:A B C D E F G
public class PrintTree {
public static void main(String[] args) {
BinaryTreeNode<String> root = new BinaryTreeNode("A");
root.left = new BinaryTreeNode("B");
root.right = new BinaryTreeNode("C");
root.left.left = new BinaryTreeNode("D");
root.left.right = new BinaryTreeNode("E");
root.right.left = new BinaryTreeNode("F");
root.right.right = new BinaryTreeNode("G");
PrintTree printTree = new PrintTree();
printTree.breadthOrderTree(root);
System.out.println("广度优先遍历");
}
/**
* 广度优先遍历
* @param root
*/
public void breadthOrderTree(BinaryTreeNode root){
if (root == null){
return;
}
Queue<BinaryTreeNode> queue = new LinkedList<BinaryTreeNode>();
queue.add(root);
while (!queue.isEmpty()){
BinaryTreeNode node = queue.poll();
System.out.print(node.val + " ");
if (node.left != null){
queue.add(node.left);
}
if (node.right != null){
queue.add(node.right);
}
}
}
private static class BinaryTreeNode<T> {
public T val;
public BinaryTreeNode left;
public BinaryTreeNode right;
public BinaryTreeNode() {
}
public BinaryTreeNode(T value) {
this.val = value;
}
public BinaryTreeNode(T val, BinaryTreeNode left, BinaryTreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
}
总结
- 树是由边和节点构成,根节点是树最顶端的节点,它没有父节点;
- 二叉树中,最多有两个子节点;
- 某个节点的左子树每个节点都比该节点的关键字值小,右子树的每个节点都比该节点的关键字值大,那么这种树称为二叉搜索树,其查找、插入、删除的时间复杂度都为logN;
- 可以通过前序遍历、中序遍历、后序遍历来遍历树,前序是根节点-左子树-右子树,中序是左子树-根节点-右子树,后序是左子树-右子树-根节点;
- 删除一个节点只需要断开指向它的引用即可;
- 哈夫曼树是二叉树,用于数据压缩算法,最经常出现的字符编码位数最少,很少出现的字符编码位数多一些。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号