数据结构与算法(三):链表
链表和数组是两个非常基础的数据结构,学习数据结构与算法都是先从学习数组和链表这两种数据结构开始。你真的了解链表这种数据结构吗?它有哪些特点?它在内存中是如何存储的?它是如何实现插入和删除操作?下面让我们带着这些问题学习链表。
什么是链表?
链表的定义
链表通过指针将一组零散的内存块串联在一起。其中,我们把内存块称为链表的节点。为了将所有的节点串起来,每个链表的节点除了存储数据之外,还需要记录链上的下一个节点的地址。如图所示,我们把这个记录下个节点地址的指针叫作后继指针 next。
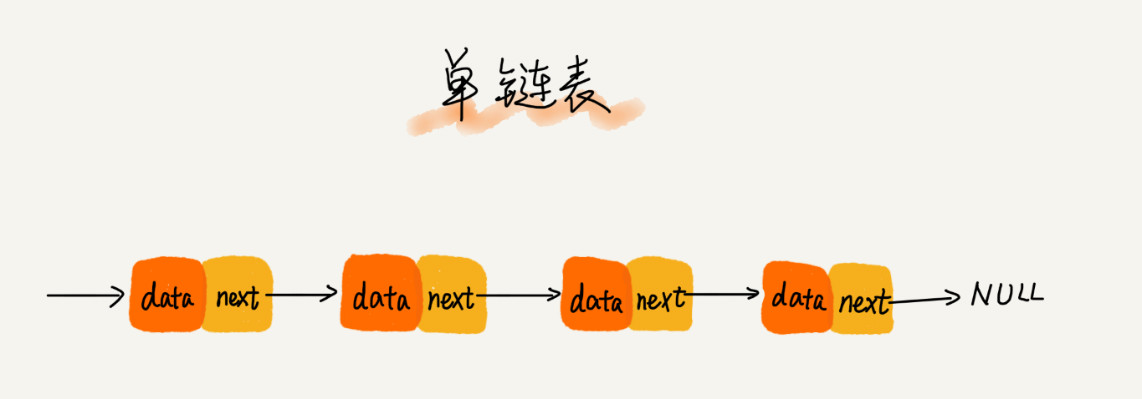
从单链表图中可以发现,其中有两个结点是比较特殊的,它们分别是第一个节点和最后一个节点。我们习惯性地把第一个结节点叫作头节点,把最后一个节点叫作尾节点。其中,头节点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而尾节点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个节点。
举例说明
类似生活中的火车,火车有火车头,中间是火车的车厢,最后一节是尾车厢,再之后就是空。
链表的分类
单向链表
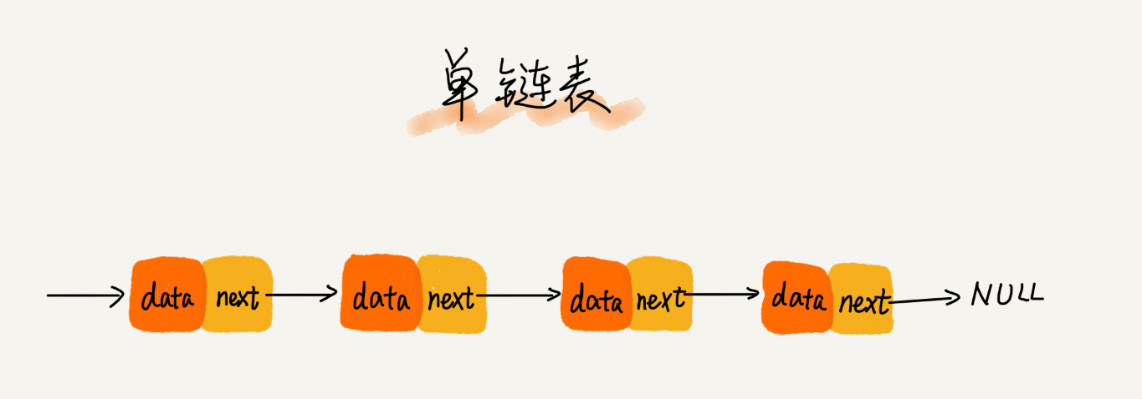
- 一个节点有一个指针域属性,指向其后继节点,尾节点的后继节点为NULL。
循环链表
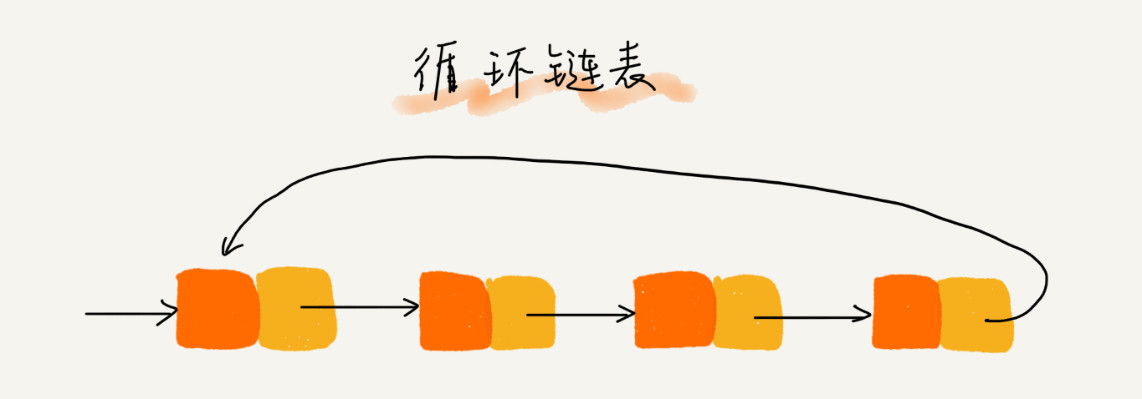
- 相比于单向链表,尾节点的后继节点为链表的首节点。
双向链表
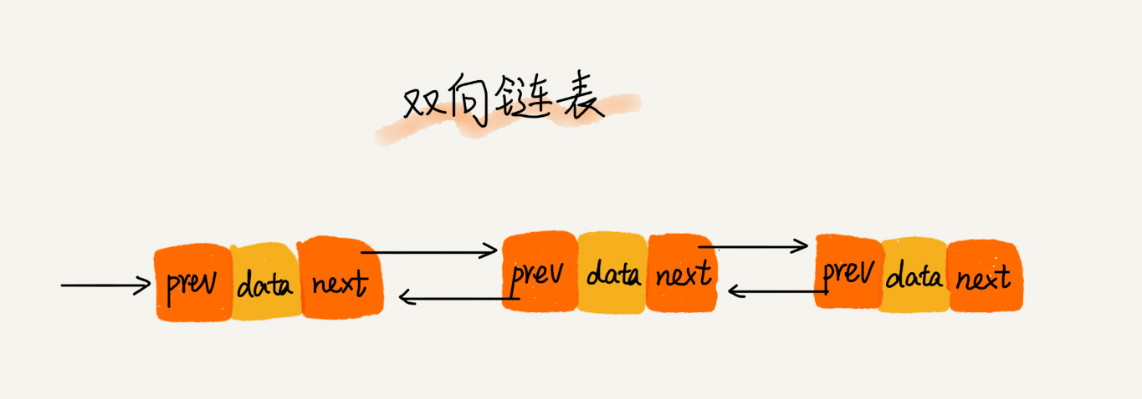
- 一个节点两个指针域属性,分别指向其前驱、后继节点,尾节点的后继节点为NULL。
双向循环链表
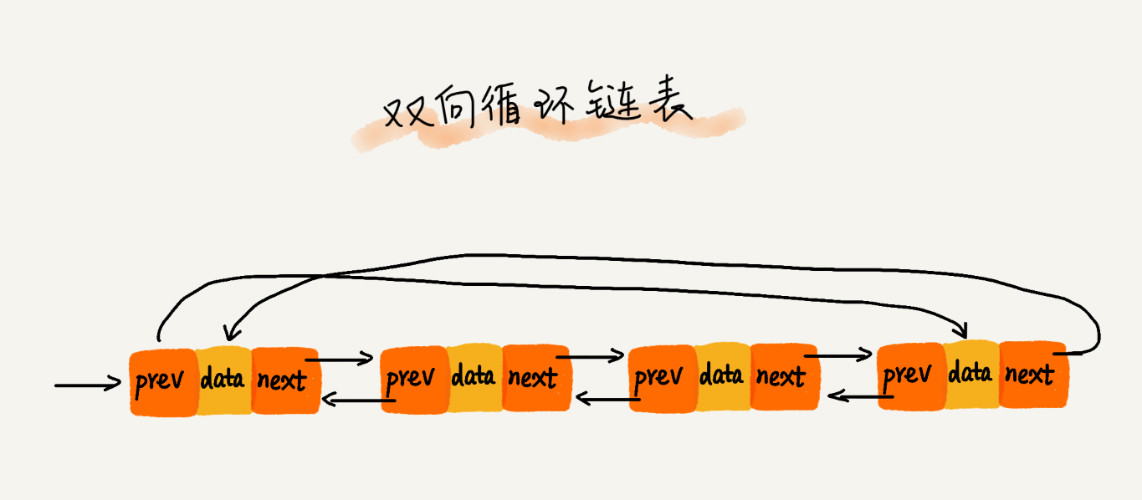
- 能通过任何一个节点找到其他所有节点,相比于双向链表,把最后一个节点的后继节点指向了第一个节点,进而形成环式循环。
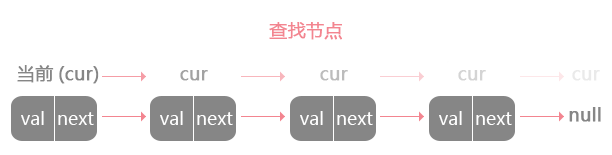
链表查询操作
链表无法像数组那样根据下标随机访问,需要从头节点开始依次遍历,所以链表的查找效率并不是很高。例如我们检查链表中是否包含某个数,需要从头节点开始遍历,这种查询操作消耗时间复杂度O(n)。
class LinkedList {
...
contains (val) {
let cur = this.head; // 不能用head遍历,会改变head的指向
while(cur != null) { // 因为尾节点指向null
if (cur.val == val) {
return true;
}
cur = cur.next; // 指向下一个节点
}
return false; // 遍历结束木有
}
}
链表插入操作
与数组添加数据向尾部添加比较方便恰恰相反,链表的添加数据从头部添加会比较方便。这里分为从头部添加,以及从头部之外的位置添加。
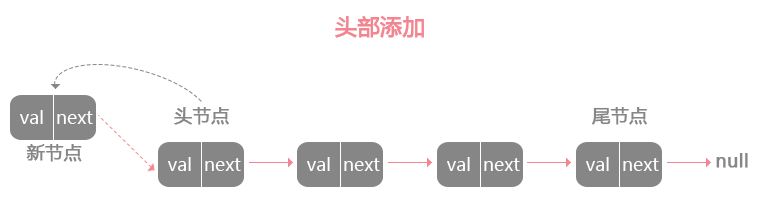
从头部添加
从头部添加新节点只需要做两件事,首先让新节点的next指针指向原先的头节点,然后将之前的头节点指向新节点,此时新节点就成为链表的头节点。这种操作时间复杂度O(1)
class LinkedList {
...
addFirst (val) {
const node = new ListNode(val)
node.next = this.head
this.head = node
// 可简写为 this.head = new ListNode(val, this.head)
}
}
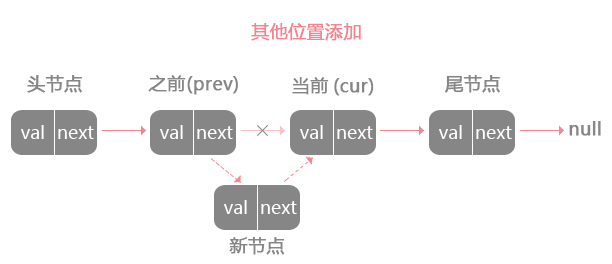
从其他位置添加
其余情况的添加节点,首先需要从头节点遍历找到待插入节点之前的节点,然后将之前节点的next指针指向新节点,新节点的指针指向待插入节点。这种操作时间复杂度O(n),因为需要先遍历查找待插入节点位置。
class LinkedList {
...
add (val, index) { // 指定下标位置添加节点
if (index < 0 || index > this.size) { // 处理越界问题
return
}
if (index == 0) { // 如果是首位添加,单独处理
this.addFirst(val)
} else {
let prev = this.head // 这里要赋值给prev,因为如果用head遍历,会改变head的指向
while(index > 1) { // 因为是找到之前的节点,所以少遍历一位
prev = prev.next // 从头依次遍历下一个节点
index--
}
const node = new ListNode(val)
// 创建一个新节点
node.next = prev.next
// 遍历结束后,prev就是之前节点,而prev.next就是待插入节点
// 让新节点指向当前节点
prev.next = node
// 之前的节点指向新节点形成链条
// 同理简写 prev.next = new ListNode(val, prev.next)
this.size++
}
}
}
这里比较麻烦,对于从头部添加以及其他位置添加需要分别的处理,因为链表头之前没有节点。而链表的编写有一个技巧就是在head指针之前,设置一个虚拟节点(也可以叫哨兵节点或哑节点),让两种操作可以统一化,我们可以这样对add方法进行改造:
class LinkedList {
...
add(val, index = 0) {
const dummy = new ListNode(); // 设置一个虚拟节点
dummy.next = this.head; // 让这个虚拟节点指向原来的头节点
let prev = dummy; // 遍历就从虚拟节点开始
while (index > 0) {
prev = prev.next;
index--;
}
prev.next = new ListNode(val, prev.next);
this.size++;
this.head = dummy.next // 虚拟头节点之后才是真实的节点,让head重新指向
}
}
通过这样的改造,之前的addFirst方法也可以不需要,默认就是从头部添加节点。
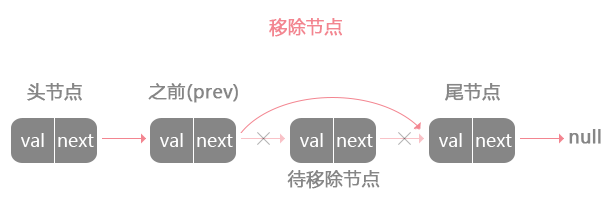
链表删除操作
如果需要删除某个节点,同理也需要找到删除节点之前的节点,让之前节点的指针指向下一个即可。这里还是 引入虚拟节点,因为删除头节点时,没有之前节点的缘故。移除头节点时间复杂度还是O(1),移除其他节点时间复杂度O(n)
class LinkedList {
...
remove(val) {
const dummy = new ListNode()
dummy.next = this.head
let prev = dummy
while(prev.next != null) {
if(prev.next.val == val) { // 找到了待移除的节点
const delNode = prev.next // 先保存待移除的节点
prev.next = delNode.next // 让之前的节点指向待移除之后的节点
delNode.next = null // 让待移除节点的指针指向空,方便GC
this.size--
break;
}
prev = prev.next // 查找下一个
}
}
}
操作链表小技巧
1、把head指针缓存起来
因为head指针始终指向的是链表的头部,而head指针又是Java里的引用类型,所以当改变cur的引用时,head的内部也会同步改变,但head始终还是头指针。
let cur = this.head
cur = cur.next // head不会有任何变化
this.head = this.head.next // 改变了头指针的位置
cur.next = null // 同样head.next也会变为null
this.head.next === null // true
2、使用虚拟节点指向头节点
这个也是上面代码使用过的技巧,这么做的原因是为了方便统一处理,然后也是不改变头指针的指向。
一般这么使用:
const dummy = new ListNode()
dummy.next = this.head
let prev = dummy
... 处理逻辑
return dummy.next
3、把赋值理解为指向
如const a = b,我们一般的理解是将b赋值给a。但如果遇到链表代码,我们需要这么解读const a = b,让a指向b,也就是从右到左的看代码变为从左到右
node.next = node.next.next
// 将node指向它的下个节点的下个节点,
// 而不要解读成将node.next.next赋值给node.next
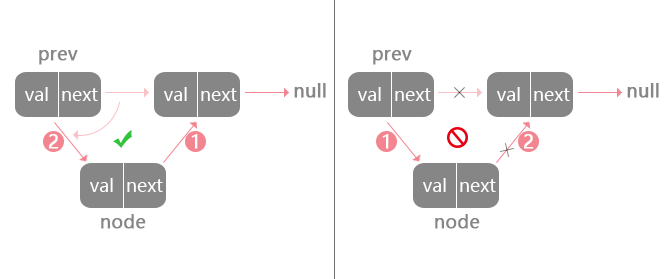
4、注意改变指针的先后顺序
例如之前插入节点的操作,首先需要让新节点指向待插入的节点,然后让之前的节点指向新节点。如果我们颠倒顺序:
颠倒顺序:
const node = new ListNode(val)
prev.next = node // 先让之前的节点指向新节点
node.next = prev.next // 然后让新节点指向待插入节点
因为这个时候prev.next已经指向了node,已经断开了和之后节点的链接,所以下一行的node.next指向的还是自己。这也说明写链表代码对逻辑性的要求,个人感觉看似简单的链表比二叉树还难理解些。
5、注意边界条件判断
当链表为空、只有一个节点、只有两个节点时,边界条件的判空要特别注意,经常遇到的问题就是指针为空的报错。
链表应用
876. 链表的中间结点
题目
给定一个带有头结点
head的非空单链表,返回链表的中间结点。如果有两个中间结点,则返回第二个中间结点。
解题分析
- 快慢指针解题法
- 存在两个指针:一个快指针,一个慢指针
- 快慢指针的起点都是链表的头节点,快指针每次走两步,慢指针每次都一步,快指针速度是慢指针2倍
- 当快指针指向null时,慢指针刚好到达链表中间位置
图解分析
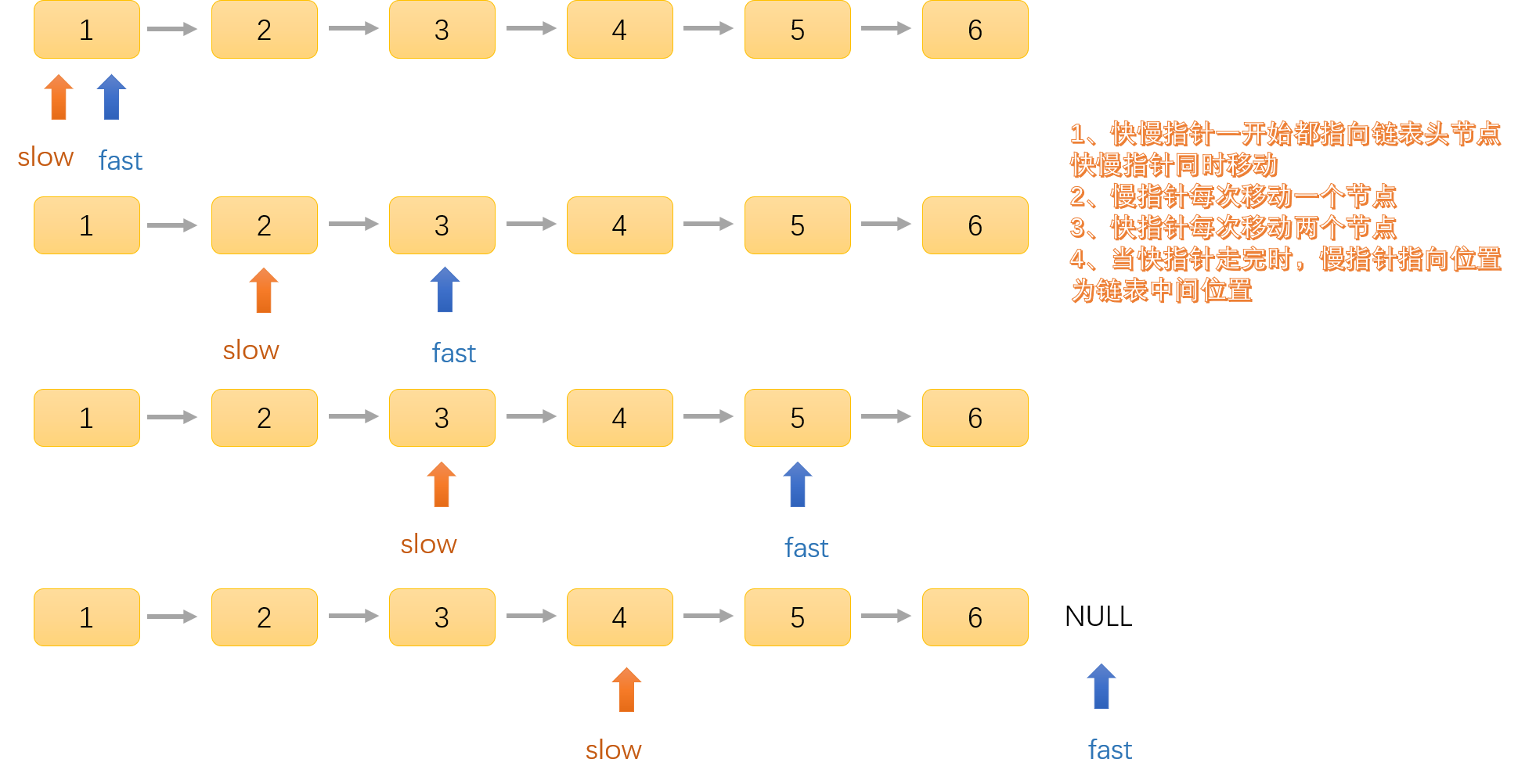
复杂度分析
时间复杂度:O(n) 其中n为链表长度,需要遍历整个链表才能得到中间位置
空间复杂度:O(1) 只需要常数空间存放 slow 和 fast 两个指针。
代码
class Solution {
public ListNode middleNode(ListNode head) {
// 1、快慢指针的起点都是链表头节点
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null){
// 2、慢指针每次走一步
slow = slow.next;
// 3、快指针是慢指针2倍速度
fast = fast.next.next;
}
return slow;
}
}
面试题 02.08. 环路检测
题目
给定一个链表,如果它是有环链表,实现一个算法返回环路的开头节点。
有环链表的定义:在链表中某个节点的next元素指向在它前面出现过的节点,则表明该链表存在环路。
25. K 个一组翻转链表
题目
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号