manacher分析

1.前言

最开始我看blog，化简式子时化简错了，理解了好久

2.算法分析

attention:

1.dp[i]表示以i为中心的回文串的长度的一半

$manacher$ 算法非常类似于暴力，只是比暴力多了一个初始化，剪掉了一下情况

暴力做法

枚举中心点，不断向外拓展，直至左右两端点不相同

首先，我们的初始化分为两种情况

(1).dp[index * 2 - i] > max - i

如图，因为 $[index-dp[index],index+dp[index]]$ (即为用黑色标出的区间)​为一个回文串，所以我们能知道，$dp[i]$ (用绿色标出的区间表示) 的最小值为 $max-i$(用蓝色标出的区间表示)​所以我们的 $dp[i]$ 可以初始化成 $max-i$

(2).dp[index * 2 - i] <= max - i

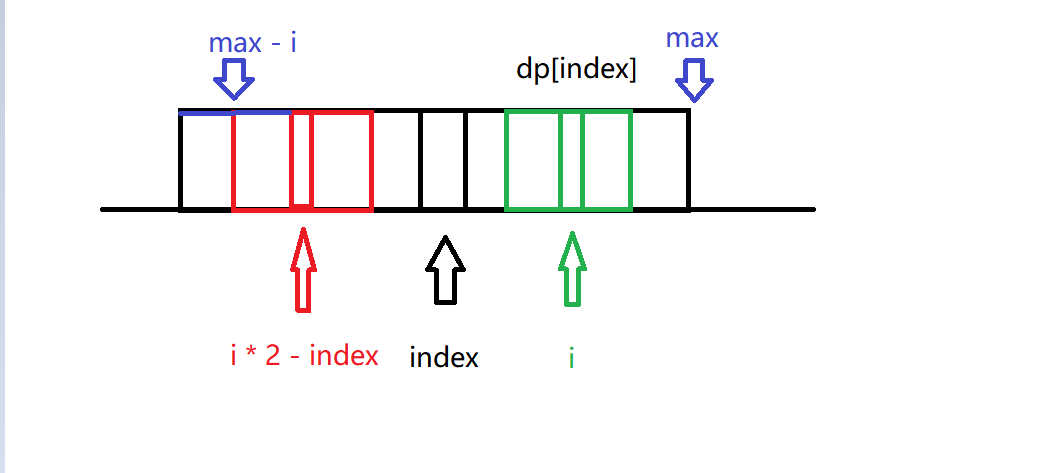
如图，同理，$dp[i]$ (用绿色标出的区间表示) 的最小值为 $dp[i\ast 2-index]$(用红色标出的区间表示)所以我们的 $dp[i]$ 可以初始化成 $dp[i\ast 2-index]$

由于会出现区间大小为偶数的情况，这个时候 $Ta$ 的重心点为空，所以我们在每两个字符中间加一个字符(例如 @)，在 $s[0]$ 处加一个不同于 刚才加的那个字符 (例如 #)(reason: 为了防止左右扩展时下表为负, $eg.$ a)，这样，就不用写两种情况了

完

真的完了？是的，就这

3.参考代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 22 * 1e6 + 5;

int dp[MAXN];
char s[MAXN], tem[MAXN];

int Min (int x, int y) { return x < y ? x : y; }
int Max (int x, int y) { return x > y ? x : y; }

int Init (char *str) {
	int len = strlen (str + 1), cnt = 0;
	tem[0] = '#';
	for (int i = 1; i <= len; i++) {
		tem[++cnt] = '@';
		tem[++cnt] = str[i];
	}
	tem[++cnt] = '@';
	memcpy (str, tem, sizeof tem);
	return cnt;
}

int Manacher (char *str) {
	int index = 0, max = 0, len = strlen (str + 1), res = 0;
	for (int i = 1; i <= len; i++) {
		if (max >= i)
			dp[i] = Min (max - i, dp[(index << 1) - i]);
		else 
			dp[i] = 0;
		while (str[i - dp[i] - 1] == str[i + dp[i] + 1]) dp[i]++;
		if (i + dp[i] > max) {
			max = i + dp[i];
			index = i;
		}
		res = Max (dp[i], res);
	}
	return res;
}

int main () {
	int step = 0;
	while (scanf ("%s", s + 1)) {
		int len = strlen (s + 1);
		if (s[1] == 'E' && s[2] == 'N' && s[3] == 'D' && len == 3) break;
		Init (s);
		printf ("Case %d: %d\n", ++step, Manacher (s));
	}
	return 0;
}