[Ceoi2016」match 题解

1.前言

和"自胡川"（手动滑稽 玩耍的出题人都是神犇

2.题解

若只要求匹配上的话，我们平时的做法就是建一个栈，对于当前元素，若栈顶元素和 $ta$ 相同，则弹出，组成一对，否则扔进栈里。

Q:区间[l,r]里的元素可以通通匹配上是什么情况？
A:遍历到 l - 1 时 和遍历到 r 时的栈内元素相同

$Wa$！！！太妙了。（出题人 $yyds$)

那就很简单了。

---

我们可以用 $Hash$ 表记录下遍历到 $i$ 的栈内元素。用递归去寻找答案

函数 $solve(l,r)$ 的作用是：匹配区间 $[l,r]$ 内的元素。

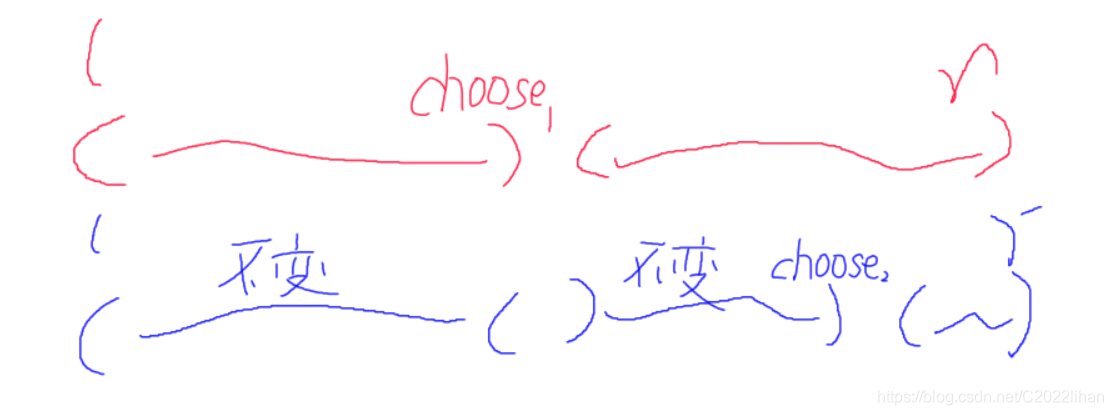
容易证明，当 $l$ 匹配的元素下标越大，则字典序越小，大概像这样就可以草草证明。

若 $l$ 能匹配 $i$
则 $i$ 满足两个条件:

1. $s[i]$ == $s[l]$
2. $Hash[i]$ == $Hash[l]$

用 $vector$ ，开两位，$g[i][j]$ 记录对应字符为 $i$，$Hash$ 值为 $j$ 的下标
二分寻找最远的 $i$ 即可。

参考代码

#include <map>
#include <stack>
#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;

#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
    x = 0; T f = 1;
    char ch = getchar ();
    while (ch < '0' || ch > '9') {
        if (ch == '-') f = -1;
        ch = getchar ();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 1) + (x << 3) + ch - '0';
        ch = getchar ();
    }
    x *= f;
}
template <typename T>
void write (T x) {
    if (x < 0) {
        putchar ('-');
        x = -x;
    }
    if (x < 10) {
        putchar (x + '0');
        return;
    }
    write (x / 10);
    putchar (x % 10 + '0');
}
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }

const int Maxn = 1e5;
const int Maxkind = 26;
const ULL P = 31;

int a[Maxn + 5];
ULL Hash[Maxn + 5];
char s[Maxn + 5];

int Top;
ULL pre[Maxn + 5];
char st[Maxn + 5];

vector <ULL> v;
vector <int> g[Maxkind + 5][Maxn + 5];
int Find (ULL x) {
	return lower_bound (v.begin (), v.end (), x) - v.begin () + 1;
}

#define ch (s[l] - 'a' + 1) 
char ans[Maxn + 5];
void solve (int l, int r) {
	if (l > r) return;
	int L = 0, R = (int)g[ch][Hash[l]].size () - 1, last;
	while (L + 1 < R) {
		int mid = L + R >> 1;
		if (g[ch][Hash[l]][mid] > r) R = mid;
		else L = mid;
	}
	if (g[ch][Hash[l]][R] <= r) last = g[ch][Hash[l]][R];
	else last = g[ch][Hash[l]][L];
	//二分寻找最远的 i (last) 
	ans[l] = '(';
	ans[last] = ')';
	solve (l + 1, last - 1);
	solve (last + 1, r);
}

int main () {
	scanf ("%s", s + 1);
	int len = strlen (s + 1);
	
	for (int i = 1; i <= len; i++) {
		if (st[Top] == s[i]) {
			Hash[i] = pre[Top];
			Top--;
			//attention：87 88 不交换位置，代码量 -= Inf 
		}
		else {
			st[++Top] = s[i];
			pre[Top] = pre[Top - 1] * P + st[Top] - 'a' + 1;
			Hash[i] = pre[Top];
		}
	}
	
	if (Top) {
		printf ("-1");
		return 0;
	}
	
	for (int i = 1; i <= len; i++) {
		v.push_back (Hash[i]);
	}
	sort (v.begin (), v.end ());
	v.erase (unique (v.begin (), v.end ()), v.end ());
	for (int i = 1; i <= len; i++) {
		Hash[i] = Find (Hash[i]);
		g[s[i] - 'a' + 1][Hash[i]].push_back (i);
	}
	//Hash过大，离散化一下 
	
	solve (1, len);
	for (int i = 1; i <= len; i++) {
		printf ("%c", ans[i]);
	}
    return 0;
}