初二20210605综合测试 心路历程 +题解
25min:乱搞T1后,果断放弃 T1
//判断正确
40min: 看完所有题,立马决定写 T4
//判断正确
70min: 写完 T4
//很遗憾,没考虑好 -1 的情况,绑点绑成零分。(主要还是 T1 没做出来,心态不好)
190min: 疯狂修改 T2
//本场考试重大失误(关键是我的代码还是对的,只是输出慢了。。。
195min: 写完 T1 暴力
//判断正确
205min: 写出 T1 正解
230min: 写完 T3 暴力
//判断正确
整场考试,大部分的抉择都是正确的,T2 的失利让我整个崩掉,所以,一些优势很容易就会因为一个小错误而全部输掉,甚至处于极大的劣势。
本场重点:
1.输入输出(你别笑。
2.对局势的判断。
下面两份代码的差别就只有输出
代码1
#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 6 * 1e6;
const int Maxkind = 10;
int n, m, k;
char a[Maxn + 5], b[Maxn + 5];
char ans1[Maxn + 5], ans2[Maxn + 5], ans3[Maxn + 5], ans4[Maxn + 5];
queue <int> q[Maxkind + 5];
int solve (char *s, char *ans, int len) {
for (int i = 1; i <= Maxkind; i++)
while (q[i].size ())
q[i].pop ();
for (int i = 1; i <= len; i++)
q[s[i] - '0'].push (i);
if (len <= k) {
for (int i = 1; i <= len; i++)
ans[i] = s[i];
return len;
}
int Need = k, p = 0, Up = Maxkind;
for (int i = 1; i <= len && Need; i++) {
//[i, len - Need + 1]
int idx = -1;
for (int j = Up; j >= 0; j--) {
while (q[j].size () && q[j].front () < i)
q[j].pop ();
if (q[j].size () && q[j].front () <= len - Need + 1) {
idx = q[j].front ();
break;
}
Up--;
}
Need--;
ans[++p] = s[idx];
i = idx;
if (s[len - Need + 1] - '0' > Up) {
for (int j = len - Need + 1; j <= len; j++)
ans[++p] = s[j];
return p;
}
}
return p;
}
signed main () {
// freopen ("password.in", "r", stdin);
// freopen ("password.out", "w", stdout);
read (n); read (m); read (k);
scanf ("%s %s", a + 1, b + 1);
for (int i = 1; i <= m; i++)
a[i + n] = b[i];
for (int i = 1; i <= n; i++)
b[i + m] = a[i];
int len1 = solve (a, ans1, n + m);
int len2 = solve (b, ans2, n + m);
bool comp = 0;
for (int i = 1; i <= len1; i++) {
if (ans1[i] > ans2[i]) {
comp = 1;
break;
}
if (ans2[i] > ans1[i]) {
comp = 0;
break;
}
}
if (comp == 1)
for (int i = 1; i <= len1; i++)
printf ("%c", ans1[i]);
else
for (int i = 1; i <= len2; i++)
printf ("%c", ans2[i]);
return 0;
}
#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 6 * 1e6;
const int Maxkind = 10;
int n, m, k;
char a[Maxn + 5], b[Maxn + 5];
char ans1[Maxn + 5], ans2[Maxn + 5], ans3[Maxn + 5], ans4[Maxn + 5];
int hh[Maxkind + 5], tt[Maxkind + 5], q[Maxkind + 5][Maxn + 5];
int solve (char *s, char *ans, int len) {
for (int i = 1; i <= Maxkind; i++)
hh[i] = 1, tt[i] = 0;
for (int i = 1; i <= len; i++)
q[s[i] - '0'][++tt[s[i] - '0']] = i;
if (len <= k) {
for (int i = 1; i <= len; i++)
ans[i] = s[i];
return len;
}
int Need = k, p = 0, Up = Maxkind;
for (int i = 1; i <= len && Need; i++) {
//[i, len - Need + 1]
int idx = -1;
for (int j = Up; j >= 0; j--) {
while (hh[j] <= tt[j] && q[j][hh[j]] < i)
hh[j]++;
if (hh[j] <= tt[j] && q[j][hh[j]] <= len - Need + 1) {
idx = q[j][hh[j]++];
break;
}
Up--;
}
Need--;
ans[++p] = s[idx];
i = idx;
if (s[len - Need + 1] - '0' > Up) {
for (int j = len - Need + 1; j <= len; j++)
ans[++p] = s[j];
return p;
}
}
return p;
}
signed main () {
// freopen ("password.in", "r", stdin);
// freopen ("password.out", "w", stdout);
read (n); read (m); read (k);
scanf ("%s %s", a + 1, b + 1);
for (int i = 1; i <= m; i++)
a[i + n] = b[i];
for (int i = 1; i <= n; i++)
b[i + m] = a[i];
int len1 = solve (a, ans1, n + m);
int len2 = solve (b, ans2, n + m);
bool comp = 0;
for (int i = 1; i <= len1; i++) {
if (ans1[i] > ans2[i]) {
comp = 1;
break;
}
if (ans2[i] > ans1[i]) {
comp = 0;
break;
}
}
if (comp == 1)
printf ("%s", ans1 + 1);
else
printf ("%s", ans2 + 1);
return 0;
}
时间对比 (在柠檬上我甚至跑了12s)
代码1

代码2

如果没有花大量时间在 T2 上,那么分数肯定也会大幅提升,虽然这个点已经被强调过无数次了,但主要的原因还是在于见识太少了,如果 我早点知道 %c & %s 时间的巨大差异,我也不会在这里强调如果了…
悲伤的小结部分过去啦,现在应该进入快乐的题解部分
T1.军训列队
很难。但是一听正解就会了,这正是思维题的魅力所在吧。
记 F ( i , j ) F (i, j) F(i,j) 表示第 i i i 列,第 j j j 行的精神值。
F ( i , j ) = i 2 + i j + j 2 + ( i − j ) ∗ 1 0 4 F (i, j) = i ^ 2 + ij + j ^ 2 + (i - j) * 10^4 F(i,j)=i2+ij+j2+(i−j)∗104
F ( i + 1 , j ) − F ( i , j ) = 2 i + 1 + j + 1 0 4 > 0 F (i + 1, j) - F (i, j) = 2i + 1 + j + 10 ^ 4 > 0 F(i+1,j)−F(i,j)=2i+1+j+104>0
所以对于每一列的同学的精神值都有单调性。
二分答案,统计精神值大于 m i d mid mid 的同学的人数,统计时,枚举每一列,二分知道第一个满足的同学即可
#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 1e6;
const LL Inf = 0x3f3f3f3f3f;
int n, m;
LL k, a[Maxn + 5];
LL solve (LL i, LL j) {
return i * i + (i - j) * 100000 + j * j + i * j;
}
LL check (LL x) {
LL ans = 0;
for (int j = 1; j <= m; j++) {
int l = 1, r = n + 1;
while (l + 1 < r) {
int mid = l + r >> 1;
if (solve (mid, j) >= x) r = mid;
else l = mid;
}
if (solve (l, j) >= x) ans += n - l + 1;
else ans += n - r + 1;
}
return ans;
}
signed main () {
// freopen ("array.in", "r", stdin);
// freopen ("array.out", "w", stdout);
read (n); read (m); read (k);
LL l = -Inf, r = Inf;
while (l + 1 < r) {
LL mid = l + r >> 1;
if (check (mid) >= k) l = mid;
else r = mid;
}
if (check (r) == k) write (r);
else write (l);
return 0;
}
T2.破解密码
y z k yzk yzk 巨佬的思路实在是太妙了,比我这个 s b sb sb 思路好了太多,在这里膜拜。
(之后说的选数都是:先选的就排在前面,即从左往右选择子序列)
容易想到:
1.将
A
A
A,
B
B
B 序列先合并起来。成为
A
B
AB
AB 和
B
A
BA
BA,比较两者大小(
t
r
y
m
y
e
d
g
e
trymyedge
trymyedge巨佬已证)
2.我们选数时,尽可能先选大的。
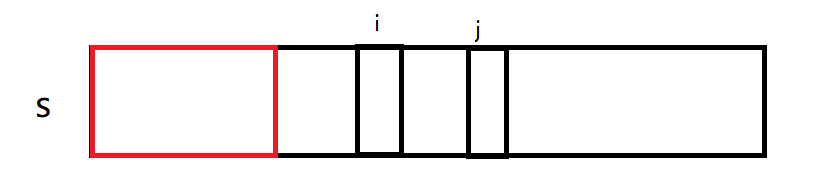
例如上图,假设红色部分的选择部分一样,若
s
[
i
]
>
s
[
j
]
s[i] > s[j]
s[i]>s[j] 则
i
i
i 序列的字典序一定大于
j
j
j 序列
3.
如果
A
A
A 的位数多余
B
B
B ,则
A
>
B
A > B
A>B (不考虑前导零的情况)
有了性质,我们开始做题了。
对于 2 2 2, 3 3 3 条性质。我们应先满足第 3 3 3 条。
N e e d Need Need 表示还要选择的数的个数, l e n len len 表示字符串的总长度。
则我们一定不能选择 ( l e n − N e e d + 1 , l e n ] (len - Need + 1, len] (len−Need+1,len] 内的数,因为选择其中的数的话,我们接下来选择的数的个数就一定到达不了 N e e d − 1 Need - 1 Need−1 个了

如图,我们只能选择红色部分。
那么我们只需要选择 [ i , l e n − N e e d + 1 ] [i, len - Need + 1] [i,len−Need+1] 里的最大最靠左的点就行了。
怎样求解最大最靠右的点呢?
我们可以将值为 i i i 的点压入队列 q [ i ] q[i] q[i], U p Up Up 表示区间内最大的值,每次我们从 q [ U p ] q[Up] q[Up] 里取出一个在区间中的值即可。如果队列中没有数满足,则 U p − − Up-- Up−−。
重点来了:当我们选择了一个数后,区间右端点向右移一位(因为 N e e d Need Need 减 1 1 1 了)。若 s [ l e n − N e e d + 1 ] > U p s[len - Need + 1] > Up s[len−Need+1]>Up, 则下一次我们只可能选择 l e n − N e e d + 1 len - Need + 1 len−Need+1, 所以我们必须选择区间 [ l e n − N e e d + 1 , l e n ] [len - Need + 1, len] [len−Need+1,len] 了。若 s [ l e n − N e e d + 1 ] ≤ U p s[len - Need + 1] \leq Up s[len−Need+1]≤Up, 则后面我们 U p Up Up 变化时一定会枚举到,就不需要管了。
#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 6 * 1e6;
const int Maxkind = 10;
int n, m, k;
char a[Maxn + 5], b[Maxn + 5];
char ans1[Maxn + 5], ans2[Maxn + 5], ans3[Maxn + 5], ans4[Maxn + 5];
int hh[Maxkind + 5], tt[Maxkind + 5], q[Maxkind + 5][Maxn + 5];
int solve (char *s, char *ans, int len) {
for (int i = 1; i <= Maxkind; i++)
hh[i] = 1, tt[i] = 0;
for (int i = 1; i <= len; i++)
q[s[i] - '0'][++tt[s[i] - '0']] = i;
if (len <= k) {
for (int i = 1; i <= len; i++)
ans[i] = s[i];
return len;
}
int Need = k, p = 0, Up = Maxkind;
for (int i = 1; i <= len && Need; i++) {
//[i, len - Need + 1]
int idx = -1;
for (int j = Up; j >= 0; j--) {
while (hh[j] <= tt[j] && q[j][hh[j]] < i)
hh[j]++;
if (hh[j] <= tt[j] && q[j][hh[j]] <= len - Need + 1) {
idx = q[j][hh[j]++];
break;
}
Up--;
}
Need--;
ans[++p] = s[idx];
i = idx;
if (s[len - Need + 1] - '0' > Up) {
for (int j = len - Need + 1; j <= len; j++)
ans[++p] = s[j];
return p;
}
}
return p;
}
signed main () {
// freopen ("password.in", "r", stdin);
// freopen ("password.out", "w", stdout);
read (n); read (m); read (k);
scanf ("%s %s", a + 1, b + 1);
for (int i = 1; i <= m; i++)
a[i + n] = b[i];
for (int i = 1; i <= n; i++)
b[i + m] = a[i];
int len1 = solve (a, ans1, n + m);
int len2 = solve (b, ans2, n + m);
bool comp = 0;
for (int i = 1; i <= len1; i++) {
if (ans1[i] > ans2[i]) {
comp = 1;
break;
}
if (ans2[i] > ans1[i]) {
comp = 0;
break;
}
}
if (comp == 1)
printf ("%s", ans1 + 1);
else
printf ("%s", ans2 + 1);
return 0;
}
T3. HH去散步
可以发现两道题的差异只在于不能走回头路, 可以有两种做法(代码应该差不多,但思路差别很大),一种是 t r y m y e d g e trymyedge trymyedge 巨佬的 d p dp dp 优化法, t r y m y e d g e trymyedge trymyedge 巨佬的题解已经十分清楚,这里不再赘述,我就讲一讲把路径做矩阵元素的做法。
加速矩阵 “连边” (即建邻接矩阵) 的原理可以参考我的 blog 的 2. ( 1 ) 2.(1) 2.(1)
把每一个无向边拆成两个有向边 i i i 和 i + m i + m i+m ,则 c [ 1 ] [ j ] c[1][j] c[1][j] 表示停留在路径 j j j 上的方案总数(注意:没有走到路径的对应点上,但也相当于走到了 j j j 的终点)。则除了 i i i 和 i + m i + m i+m 不能“连边”以外(不走回头路),对于其他的任意两条边 i ( x i → y i ) i (x_i \rightarrow y_i) i(xi→yi), j ( x j → y j ) j (x_j \rightarrow y_j) j(xj→yj),若 y i = x j y_i = x_j yi=xj(即可以从 i i i 路径走到 j j j 路径),则连上一条边。
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 20;
const int Maxm = 120;
const int Mod = 45989;
int n, m, s, t;
LL k;
struct date {
int x, y;
}d[Maxm + 5];
struct Matrix {
int n, m;
int c[Maxm + 5][Maxm + 5];
Matrix () {
memset (c, 0, sizeof c);
}
void Init () {
for (int i = 1; i <= n; i++)
c[i][i] = 1;
}
};
Matrix operator * (Matrix x, Matrix y) {
Matrix ans; ans.n = x.n; ans.m = y.m;
for (int i = 1; i <= ans.n; i++)
for (int j = 1; j <= ans.m; j++)
for (int k = 1; k <= x.m; k++)
ans.c[i][j] = (ans.c[i][j] + x.c[i][k] * y.c[k][j]) % Mod;
return ans;
}
Matrix quick_pow (Matrix a, LL b) {
Matrix ans;
ans.n = m * 2; ans.m = m * 2; ans.Init ();
while (b) {
if (b & 1) ans = ans * a;
a = a * a; b >>= 1;
}
return ans;
}
signed main () {
read (n); read (m); read (k); read (s); read (t);
for (int i = 1; i <= m; i++) {
read (d[i].x); read (d[i].y);
d[i + m].x = d[i].y; d[i + m].y = d[i].x;
}
Matrix a, b; b.n = m * 2; b.m = m * 2;
//a为答案矩阵,b为加速矩阵
for (int i = 1; i <= m * 2; i++)
for (int j = 1; j <= m * 2; j++)
if (d[i].y == d[j].x && Abs (i - j) != m && i != j)
b.c[i][j] = 1;//如果i号路径可以走到j号路径,则“连边”
a.n = 1; a.m = m * 2;
for (int i = 1; i <= a.m; i++)
if (d[i].x == s)
a.c[1][i] = 1;
Matrix ans = a * quick_pow (b, k - 1);
int res = 0;
for (int i = 1; i <= ans.m; i++)
if (d[i].y == t)
res = (res + ans.c[1][i]) % Mod;
write (res);
return 0;
}
T4.现代豪宅
这道题其实是一道又板代码量又不是特别大的题,结果许多巨佬没有看到
这道题是由两道题拼接拼接而成的 回家(T4) (截取了 ta 巧妙的连边) 和 虫洞(截取了 ta 巧妙的分层图思想)。
1.建图
(1)节点
如果 ( 1 , 1 ) (1, 1) (1,1) 上有点存在,则记录下 ta 的编号,否则建立一个虚拟节点 0 0 0。
把开关当作图的节点,则我们多建点 i + m i + m i+m,表示走到 i i i 号开关时,这时候所有的门都是竖着的关闭,同理,点 i i i 表示走到 i i i 号开关时,这时候所有的门都是横着的关闭。
(2)连边
先将所有的 i i i 和 i + m i + m i+m 相连,代价为 1 1 1 (打开开关,切换门的方向)
将所有的开关按照 x x x 为第一关键字, y y y 为第二关键字排序,对于相邻的两点 i − 1 i - 1 i−1, i i i, 如果满足 x i − 1 = x i x_{i - 1} = x_i xi−1=xi , 则连边 ( i − 1 ) . i d (i - 1).id (i−1).id 和 i . i d i.id i.id ( i d id id 表示排序前的下标)。
再将所有的开关按照 y y y 为第一关键字, x x x 为第二关键字排序,对于相邻的两点 i − 1 i - 1 i−1, i i i, 如果满足 y i − 1 = y i y_{i - 1} = y_i yi−1=yi , 则连边 ( i − 1 ) . i d + m (i - 1).id + m (i−1).id+m 和 i . i d + m i.id + m i.id+m ( i d id id 表示排序前的下标)。
为什么这样连边呢?
如图

若正确的走法为 i → k i \rightarrow k i→k, 则可以拆成 i → j i \rightarrow j i→j, j → k j \rightarrow k j→k(巧妙的连边)。
最后跑最短路就行了。统计答案的话就枚举所有开关,如果走得到这个开关(我考试就没写这个,可我记得我写了??)且走得到点
(
n
,
n
)
(n, n)
(n,n),则计算 ta 的答案。
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
#define int long long
#define LL long long
#define ULL unsigned long long
template <typename T>
void read (T &x) {
x = 0; T f = 1;
char ch = getchar ();
while (ch < '0' || ch > '9') {
if (ch == '-') f = -1;
ch = getchar ();
}
while (ch >= '0' && ch <= '9') {
x = (x << 3) + (x << 1) + ch - '0';
ch = getchar ();
}
x *= f;
}
template <typename T>
void write (T x) {
if (x < 0) {
x = -x;
putchar ('-');
}
if (x < 10) {
putchar (x + '0');
return;
}
write (x / 10);
putchar (x % 10 + '0');
}
template <typename T>
void print (T x, char ch) {
write (x); putchar (ch);
}
template <typename T> T Abs (T x) { return x > 0 ? x : -x; }
template <typename T> T Max (T x, T y) { return x > y ? x : y; }
template <typename T> T Min (T x, T y) { return x < y ? x : y; }
const int Maxn = 2 * 1e5;
const LL Inf = 0x3f3f3f3f3f3f3f;
int n, m, k, idx;
struct Node {
int x, y, id;
}a[Maxn * 2 + 10], b[Maxn * 2 + 10];
bool cmpx (Node x, Node y) {
if (x.x != y.x) return x.x < y.x;
else return x.y < y.y;
}
bool cmpy (Node x, Node y) {
if (x.y != y.y) return x.y < y.y;
else return x.x < y.x;
}
struct edge {
int len, Head[Maxn * 2 + 10];
int to[Maxn * 8 + 10], Next[Maxn * 8 + 10];
LL val[Maxn * 8 + 10];
void Init () {
len = 1;
memset (Head, 0, sizeof Head);
}
void plus (int x, int y, LL VAL) {
to[++len] = y;
Next[len] = Head[x];
val[len] = VAL;
Head[x] = len;
}
void add (int x, int y, LL VAL) {
plus (x, y, VAL);
plus (y, x, VAL);
}
}mp;
struct Date {
int u;
LL val;
Date () {}
Date (int U, LL VAL) {
u = U; val = VAL;
}
};
bool operator < (Date x, Date y) {
return x.val > y.val;
}
priority_queue <Date> q;
LL dist[Maxn * 2 + 10];
bool vis[Maxn * 2 + 10];
void dijkstra () {
memset (dist, 0x3f, sizeof dist);
if (idx != 0) {
dist[idx] = 0;
q.push (Date (idx, 0));
}
else {
dist[0] = 0;
q.push (Date (0, 0));
}
while (q.size ()) {
Date tem = q.top (); q.pop ();
int u = tem.u;
if (vis[u] == 1) continue;
vis[u] = 1;
for (int i = mp.Head[u]; i; i = mp.Next[i]) {
int v = mp.to[i], w = mp.val[i];
if (vis[v] == 1) continue;
if (dist[v] > dist[u] + w) {
dist[v] = dist[u] + w;
q.push (Date (v, dist[v]));
}
}
}
}
signed main () {
// freopen ("building.in", "r", stdin);
// freopen ("building.out", "w", stdout);
mp.Init ();
read (n); read (m); read (k);
for (int i = 1; i <= k; i++) {
read (a[i].x); read (a[i].y);
a[i].id = i; b[i] = a[i];
b[i + k] = b[i];
if (a[i].x == a[i].y && a[i].x == 1)
idx = i;
}
sort (a + 1, a + 1 + k, cmpx);
if (a[1].x == 1) mp.add (0, a[1].id, a[1].y - 1);
for (int i = 1; i <= k; i++)
mp.add (a[i].id, a[i].id + k, 1);
for (int i = 2; i <= k; i++)
if (a[i].x == a[i - 1].x)
mp.add (a[i - 1].id, a[i].id, a[i].y - a[i - 1].y);
sort (a + 1, a + 1 + k, cmpy);
for (int i = 2; i <= k; i++)
if (a[i].y == a[i - 1].y)
mp.add (a[i - 1].id + k, a[i].id + k, a[i].x - a[i - 1].x);
dijkstra ();
LL ans = Inf; bool flag = 0;
for (int i = 1; i <= k * 2; i++) {
if (vis[i] == 0) continue;
if (b[i].x == n) {
flag = 1;
ans = Min (ans, dist[i] + m - b[i].y + (i <= k ? 0 : 1));
}
if (b[i].y == m) {
flag = 1;
ans = Min (ans, dist[i] + n - b[i].x + (i <= k ? 1 : 0));
}
}
if (flag == 0) printf ("-1");
else write (ans);
return 0;
}



