经典基础算法之BST详解(系列二)
4. 二叉查找树(BST)
4.1 BST数据结构定义
使用C++语言,如果需要使用BST,那么不用重新造轮子了,C++语言里的map, set等STL容器应该可以满足需求了(虽然STL里这些容器大多是以红黑树作为其底层实现),如果你需要使用小/大根堆(也叫优先队列,特殊的、自平衡的BST),STL也能满足你的需求(可以参考这里:http://www.cnblogs.com/dskit/archive/2009/12/13/1623152.html)。
先来看下BST的定义,BST是满足如下3个条件的二叉树:
1. 节点的左子树包含的节点的值小于该节点的值
2. 节点的右子树包含的节点的值大于等于该节点的值
3. 节点的左子树和右子树都是BST
BST的数据结构包含指向左右孩子的指针,以及一个指向节点父节点的指针(该指针在删除节点的时候可以用于快速获取其父节点,从而简化操作)。BST的初始构建可以利用插入操作完成,BST最常使用的操作是查找和遍历,还有删除操作但相对较少使用;删除操作是BST支持的几种操作中实现难度最大的,下面我们依次介绍这BST的插入、查询、遍历和删除操作。
1: #ifndef _BINARY_SEARCH_TREE_H
2: #define _BINARY_SEARCH_TREE_H
3: #include <stdio.h>
4:
5: /* 关键值比较函数 */
6: typedef int (*bstCmp)(void *left, void *right);
7:
8: /* 遍历树时的处理函数 */
9: typedef void (*bstKeyHandler)(void *key, int key_len);
10:
11: typedef struct bst {
12: struct bst *left;
13: struct bst *right;
14: /* 使用parent域的原因:在删除节点时可以快速获得被删除节点的父节点 */
15: struct bst *parent;
16: /* 关键值,可以是包含了丰富内容的结构 */
17: void *key;
18: /* key所指向空间的长度 */
19: int key_len;
20: } bst;
21:
22: typedef enum TraverseType {
23: TRAVERSE_TYPE_MID, /* 中序遍历 */
24: TRAVERSE_TYPE_PRE, /* 前序遍历 */
25: TRAVERSE_TYPE_SUF /* 后序遍历 */
26: } TraverseType;
27:
28: bst *bstSearch(bst *root, void *key, bstCmp cmp);
29: bst *bstInsert(bst *root, void *key, int key_len, bstCmp cmp);
30: int bstDelete(bst *root, void *key, bstCmp cmp);
31: void bstTraverse(bst *root, bstKeyHandler handler, TraverseType type);
32: #endif
33:
4.2 BST的插入
插入操作类似于查找,是个递归过程,只不过插入操作在查找不到的时候创建一个新节点并将其加入树,需考虑下面4种情形:
1. 当前节点的关键值等于待插入节点关键值,则不做任何处理(若需要可更新该节点),返回;
2. 当前节点的关键值小于待插入节点关键值,根据BST的定义,待插入节点应插入当前节点的左子树:
a) 若当前节点的左子树为空,则待插入节点应为当前节点的左孩子,新建节点并插入,
b) 若当前节点的左子树非空,则递归插入;
3. 当前节点的关键值大于待插入节点关键值,根据BST的定义,待插入节点应插入当前节点的右子树:
a) 若当前节点的右子树为空,则待插入节点应为当前节点的右孩子,新建节点并插入,
b) 若当前节点的右子树非空,则递归插入;
4. 若当前节点为空,则说明当前为空树,待插入节点应为树根。
1: bst *bstNewNode(void *key, int key_len, bst *parent)
2: {
3: bst *new = (bst *)calloc(1, sizeof(bst));
4: if (NULL == new) {
5: abort();
6: }
7: new->key = calloc(1, key_len);
8: if (NULL == new->key) {
9: abort();
10: }
11: new->key = key;
12: new->key_len = key_len;
13: new->parent = parent;
14: memmove(new->key, key, key_len);
15:
16: return new;
17: }
18:
19: bst *bstInsert(bst *root, void *key, int key_len, bstCmp cmp)
20: {
21: if (NULL == root) { /* 该分支处理根节点插入 */
22: return bstNewNode(key, key_len, NULL);
23: }
24:
25: int ret = cmp(root->key, key);
26: if (0 == ret) {
27: return root; /* 关键值相同,不更新该元素,如需要可更新该节点 */
28: } else if (0 < ret) {
29: if (NULL == root->right) {
30: root->right = bstNewNode(key, key_len, root);
31: return root->right;
32: } else {
33: return bstInsert(root->right, key, key_len, cmp);
34: }
35: } else /* 0 >= ret */ {
36: if (NULL == root->left) {
37: root->left = bstNewNode(key, key_len, root);
38: return root->right;
39: } else {
40: return bstInsert(root->left, key, key_len, cmp);
41: }
42: }
43: }
4.3 BST的查找
BST的查找实现利用递归相对简单,具体实现如下:
1: bst *bstSearch(bst *root, void *key, bstCmp cmp)
2: {
3: if (NULL == root) {
4: return NULL; /* 被查找关键值不存在于树中 */
5: }
6:
7: int ret = cmp(root->key, key);
8: if (0 == ret) {
9: return root; /* 找到! */
10: } else if (0 < ret) {
11: return bstSearch(root->right, key, cmp); /* 待查找关键值大于当前节点关键值,则在当前节点的右子树中查找 */
12: } else /* 0 >= ret */ {
13: return bstSearch(root->left, key, cmp); /* 待查找关键值小于当前节点关键值,则在当前节点的左子树中查找 */
14: }
15: }
4.4 BST的遍历
遍历实现也是利用递归的思路进行;可在实现中携带type参数,用于支持的遍历方式:中序、前序或后序。下面的实现是中序遍历,若需要可实现另外两种遍历方式。
1: void bstTraverse(bst *root, bstKeyHandler handler, TraverseType type)
2: {
3: handler(root->key, root->key_len); /* handler为节点的访问处理函数 */
4:
5: if (NULL != root->left) {
6: //printf("%d's left: ", *(int *)root->key);
7: bstTraverse(root->left, handler, type);
8: }
9: if (NULL != root->right) {
10: //printf("%d's right: ", *(int *)root->key);
11: bstTraverse(root->right, handler, type);
12: }
13:
14: return ;
15: }
4.5 BST的删除
插入操作也类似于查找,是个递归过程,只不过删除操作在找到被删除节点后的处理要复杂些,需考虑下面4种情形:
1. 当前节点的关键值等于待删除关键值,则进入删除处理过程;
2. 当前节点的关键值小于待插入节点关键值,根据BST的定义,应在当前节点的左子树上递归删除操作;
3. 当前节点的关键值大于待插入节点关键值,根据BST的定义,应在当前节点的右子树上递归删除操作;
4. 若当前节点为空,则说明查找不到待删除关键值的节点,返回-1指示删除失败。
删除处理过程又需要考虑以前几种情形:
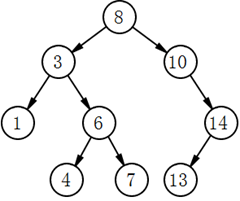
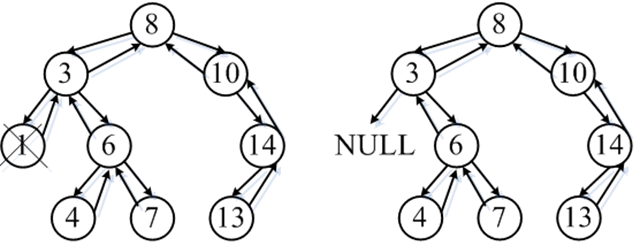
1. 待删除节点为叶子节点(左右孩子均为空);
a) 将待删除节点的父节点指向该待删除节点的指针置为空,
b) 删除待删除节点。
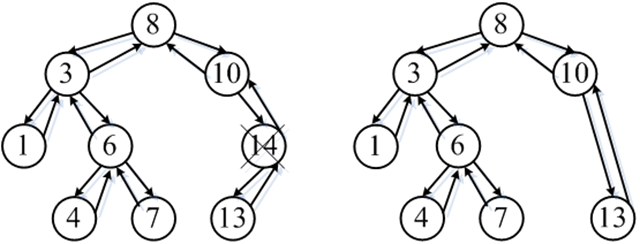
2. 待删除节点(10)为左孩子为空,右孩子非空;
a) 将待删除节点(10)的父节点(8)原来指向待删除节点(10)的指针重新指向待删除节点(10)的右孩子(14),
b) 将待删除节点(10)的右孩子节点(14)原来指向待删除节点(10)的父指针重新指向待删除节点(10)的父节点(8),
b) 删除待删除节点(10)。
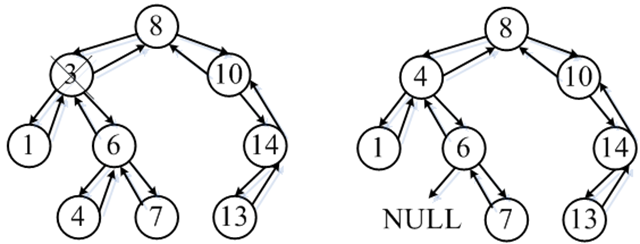
上面展示了待删除节点(10)为(8)右孩子节点的情况,由于待删除节点(10)的右孩子节点必定大于等于(10),而(10)又为(8)的右孩子,所以待删除节点(10)的右孩子节点必定大于(8),待删除节点(10)的右孩子节点可以直接取代(10)的位置作为(8)的右孩子。那么等待删除节点本身为左孩子的情况呢?请看下图,节点(3)满足本身待删除节点本身为左孩子的情况,根据BST的定义,若待删除节点(3)为左孩子,则待删除节点的所有孩子节点均小于其父节点(8),所以也可以将其右孩子节点直接作为(8)的左孩子。
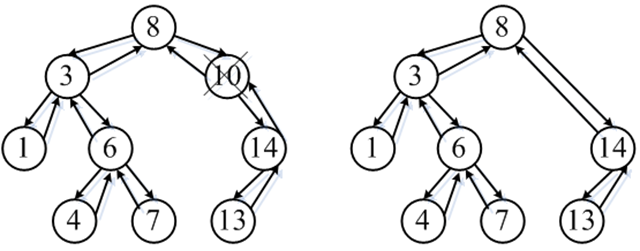
3. 待删除节点(14)为左孩子非空,右孩子为空;
a) 将待删除节点(14)的父节点(10)原来指向待删除节点(14)的指针重新指向待删除节点(10)的左孩子(13),
b) 将待删除节点(14)的左孩子节点(13)原来指向待删除节点(14)的父指针重新指向待删除节点(14)的父节点(10),
c) 删除待删除节点(14)。
可以这样操作的原因分析类似2中的分析,不再赘述。
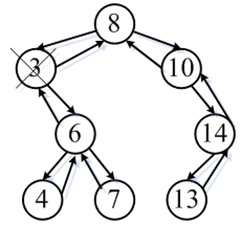
4. 待删除节点(3)为左孩子非空,右孩子非空。
a) 将待删除节点(3)的关键值与其右子树上值最小节点(4)的值交换,原节点(4)转换为待删除节点,准备被删除,
注1:待删除节点右子树上最小值节点的左孩子必为空, 否则,根据BST定义,最小值节点应在该节点的左子树上;
注2:待删除节点右子树上最小值节点的右孩子可为空,也可不为空;
注3:待删除节点与其右子树上最小值节点交换后,删除原右子树最小值节点后,仍为BST。
b) 根据注1,删除新待删除节点转换为删除叶子节点或删除只有右孩子节点的情况,本例为删除叶子节点。
另外,也可以选择待删除节点左子树上的最大值节点进行交换,处理方式与上述方式类似,读者可以自行分析;有文献称总是选择与右子树上最小值节点交换或总是选择与左子树上最大值节点交换,可能造成树的不平衡,从而使对BST的操作效率降低。
1: int bstDelete(bst *root, void *key, bstCmp cmp)
2: {
3: if (NULL == root) { /* 查找待删除关键值失败 */
4: return -1;
5: }
6:
7: int ret = cmp(root->key, key);
8: if (0 == ret) { /* 查找到待删除关键值,进入删除处理程序 */
9: if ((NULL != root->left) && (NULL != root->right)) {
10: bst *right_min = bstSearchMin(root->right);
11: bstSwap(root, right_min); /* 交换待删除关键值与该待删节点右子树上关键值最小的节点的关键值交换 */
12: if (right_min->parent->left == right_min) {
13: right_min->parent->left = right_min->right; /* 将指向当前待删除节点的指针置为当前待删除节点的右子树(这里的右子树可以为空) */
14: } else {
15: right_min->parent->right = right_min->right; /* 将指向当前待删除节点的指针置为当前待删除节点的右子树(这里的右子树可以为空) */
16: }
17: if (NULL != right_min->right) { /* 注意:这里需更新当前待删除节点右子树的父节点指针 */
18: right_min->right->parent = right_min->parent;
19: }
20: free(right_min); /* 删除待删除节点右子树上值最小的节点 */
21: } else {
22: if (NULL != root->left) {
23: if (root->parent->left == root) {
24: root->parent->left = root->left;
25: } else {
26: root->parent->right = root->left;
27: }
28: root->left->parent = root->parent;
29: } else if (NULL != root->right) {
30: if (root->parent->left == root) {
31: root->parent->left = root->right;
32: } else {
33: root->parent->right = root->right;
34: }
35: root->right->parent = root->parent;
36: } else {
37: if (root->parent->left == root) {
38: root->parent->left = NULL;
39: } else {
40: root->parent->right = NULL;
41: }
42: }
43: free(root);
44: }
45: return 0;
46: } else if(0 < ret) { /* 当前节点的关键值大于待插入节点关键值,根据BST的定义,应在当前节点的右子树上递归删除操作; */
47: return bstDelete(root->right, key, cmp);
48: } else /* 0 >= ret */ { /* 当前节点的关键值小于待插入节点关键值,根据BST的定义,应在当前节点的左子树上递归删除操作 */
49: return bstDelete(root->left, key, cmp);
50: }
51:
52: return 0;
53: }
4.6 性能分析
平均复杂度 最坏情况复杂度
插入操作 O(logN) O(N)
查询操作 O(logN) O(N)
删除操作 O(logN) O(N)
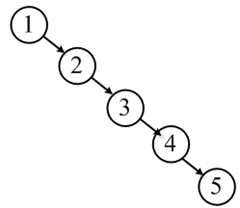
当插入节点为有序序列时,构建的树上的节点只有左孩子或右孩子,有最大复杂度O(N)。如插入有序序列(1, 2, 3, 4, 5),插入操作完成后的BST如下图:
4.7 二叉查找树应用
1. 如何合并两颗BST?
法一:遍历其中一颗BST,将其插入另一颗BST。
法二:根据两颗树的根节点选取一个虚拟的根节点,将两颗BST作为虚拟根节点的左右子树,然后对虚拟根节点进行删除操作即可。
法一的时间复杂度为O(MlogN)或O(NlogM),法二的时间复杂度为O(logN)或O(logM)。可见法二的合并效率更高。
2. 有上百万个电话号码,需要频繁的进行查找操作,怎样设计数据结构使其效果最高?
该类问题使用BST可以很好的解决,当然使用其他改进的数据结构如红黑树、字典树也是高效的解决方案。
4.8 参考文献
http://en.wikipedia.org/wiki/Binary_search_tree
本文许可自由转载,转载请注明出处!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号