noip2018day1-赛道修建
题目描述
\(C\) 城将要举办一系列的赛车比赛。在比赛前,需要在城内修建 $m $条赛道。
\(C\) 城一共有 \(n\) 个路口,这些路口编号为 \(1,2,…,n\)有 $n-1 $条适合于修建赛道的双向通行的道路,每条道路连接着两个路口。其中,第 $i $条道路连接的两个路口编号为 \(a_i\) 和 \(b_i\),该道路的长度为 \(l_i\)。借助这 \(n-1\) 条道路,从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 \(e_1,e_2,…,e_k\),满足可以从某个路口出发,依次经过 道路 \(e_1,e_2,…,e_k\)(每条道路经过一次,不允许调头)到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全,要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案,使得修建的 \(m\)条赛道中长度最小的赛道长度最大(即 \(m\) 条赛道中最短赛道的长度尽可能大)
Input
输入文件第一行包含两个由空格分隔的正整数 \(n,m\),分别表示路口数及需要修建的 赛道数。
接下来 \(n-1\) 行,第 \(i\)行包含三个正整数 \(a_i,b_i,l_i\),表示第 \(i\) 条适合于修建赛道的道 路连接的两个路口编号及道路长度。
保证任意两个路口均可通过这 \(n-1\) 条道路相互到达。
每行中相邻两数之间均由一个空格分隔。
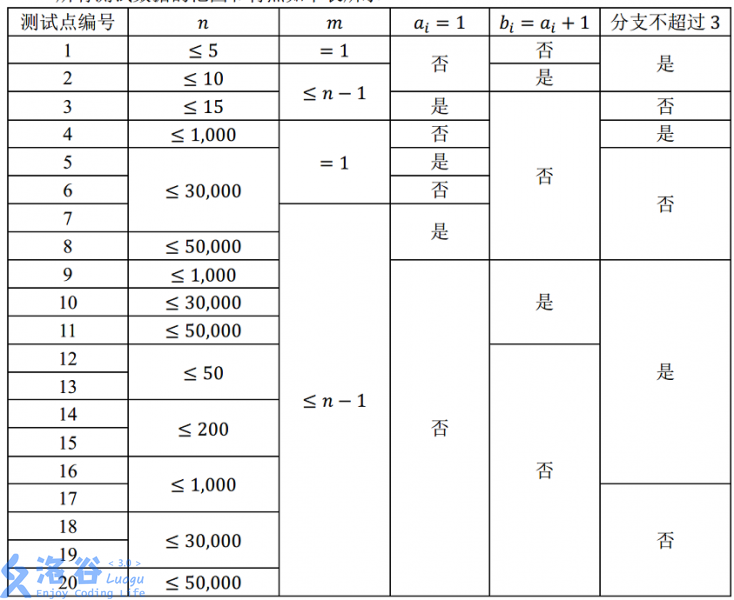
对于所有的数据, \(2 ≤ n ≤ 50,000\), \(1 ≤ m ≤ n-1\), \(1 ≤ a_i,b_i ≤ n\), \(1 ≤ l_i ≤ 10,000\)。
Output
输出共一行,包含一个整数,表示长度最小的赛道长度的最大值。
Sample Input
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
9 3
1 2 6
2 3 3
3 4 5
4 5 10
6 2 4
7 2 9
8 4 7
9 4 4
Sample Output
31
15
很自然的想到是二分。。。
话说为什么联赛有那么多二分???
最小值最大,标准的二分询问。
我们可以去二分它的最小值最大的答案,然后去\(check\)它。
怎么去\(check\)它呢?首先,我们先分析路径的状态。
一条路径在树上有两种状态:
- 挂在一个节点下面的一条链。
- 两条挂在节点下的链组成的路径。
很显然,我们需要一种方法使得所有路径长度大于等于当前\(x\)的数量最大。
我们可以发现,若以一个节点为根节点的子树有残留的形如\(1\)的链有两种选择。
- 将其和其他的链进行配对形成如同\(2\)所说的链对。
- 不满足条件\(1\),将其作为子链的一部分并到其父亲节点上。
很显然,只有这样才可以保证所有的链数量最多。
那么,我们该如何维护这个过程呢?
利用\(mutilset\)动态的维护这个过程就可以了。
当然,作为一名\(oier\)只写一个正解是不太友善的。。。万一挂了呢?
我们要切分!!!
特殊情况一:链
对于一条链,问题变成了有\(n\)个数,将其分为\(m\)个不重叠的区间并且每个区间和最大。
这个问题可以直接二分求解,\(check\)函数如下:
bool check(int x){
int Sum=0,tot=0;
rep(i,1,n){
Sum+=A[i];
if(Sum>=x)Sum=0,tot++;
}
return tot>=m;
}
特殊情况二:菊花图
对于菊花图也还是直接二分。
很显然,我们可以先将所有的边按照边权进行一波排序。
然后,我们开两个指针分别指向开头和结尾。
我们再移动指针直到其相遇。
我们可以发现,一条长度已经大于等于当前\(x\)的边可以直接当一条路径。
而未到当前长度的边可以从尾指针向前找到一个相加可以满足条件的边即可。
bool check(int x){
int posl=0,posr=cnt,tot=0;
while(posr>posl) {
if(A[posr]>=x)posr--,tot++;
else {
while(posl<posr&&A[posl]+A[posr]<x)posl++;
if(posl==posr)continue;
posr--,posl++,tot++;
}
}
return tot>=m;
}
代码如下
#include <bits/stdc++.h>
using namespace std;
#define LL long long
#define reg register
#define Raed Read
#define debug(x) cerr<<#x<<" = "<<x<<endl;
#define rep(a,b,c) for(reg int a=(b),a##_end_=(c); a<=a##_end_; ++a)
#define ret(a,b,c) for(reg int a=(b),a##_end_=(c); a<a##_end_; ++a)
#define drep(a,b,c) for(reg int a=(b),a##_end_=(c); a>=a##_end_; --a)
#define erep(i,G,x) for(int i=(G).Head[x]; i; i=(G).Nxt[i])
inline int Read() {
int res = 0, f = 1;
char c;
while (c = getchar(), c < 48 || c > 57)if (c == '-')f = 0;
do res = (res << 3) + (res << 1) + (c ^ 48);
while (c = getchar(), c >= 48 && c <= 57);
return f ? res : -res;
}
template<class T>inline bool Min(T &a, T const&b) {
return a > b ? a = b, 1 : 0;
}
template<class T>inline bool Max(T &a, T const&b) {
return a < b ? a = b, 1 : 0;
}
const int N=5e4+5,M=5e4+5,mod=1e9+7;
bool MOP1;
int n,m,L,R;
struct Link_list {
int Tot,Head[N],to[M<<1],Nxt[M<<1],cost[M<<1];
inline void clear(void) {
Tot=0;
memset(Head,0,sizeof Head);
}
inline void AddEdgepair(const int a,const int b,const int c) {
to[++Tot]=b,cost[Tot]=c,Nxt[Tot]=Head[a],Head[a]=Tot;
to[++Tot]=a,cost[Tot]=c,Nxt[Tot]=Head[b],Head[b]=Tot;
}
} G;
struct T3flower {
int Ans,cnt,A[N];
inline bool check(const int x) {
int posl=0,posr=cnt,tot=0;
while(posr>posl) {
if(A[posr]>=x)posr--,tot++;
else {
while(posl<posr&&A[posl]+A[posr]<x)posl++;
if(posl==posr)continue;
posr--,posl++,tot++;
}
}
return tot>=m;
}
inline void solve(void) {
int Ans=0;
cnt=0;
erep(i,G,1) {
int y=G.to[i];
A[++cnt]=G.cost[i];
}
sort(A+1,A+cnt+1);
while(L<=R) {
int mid=(L+R)>>1;
if(check(mid))Ans=mid,L=mid+1;
else R=mid-1;
}
printf("%d\n",Ans);
}
} Pflower;
int deg[N];
struct T3list {
int cnt,A[N];
inline bool check(const int x) {
int Sum=0,tot=0;
rep(i,1,n-1) {
Sum+=A[i];
if(Sum>=x)Sum=0,tot++;
}
return tot>=m;
}
void dfs(const int x,const int pre) {
erep(i,G,x) {
int y=G.to[i];
if(y==pre)continue;
A[++cnt]=G.cost[i];
dfs(y,x);
}
}
inline void solve(void) {
int Ha=0;
cnt=0;
rep(i,1,n)if(deg[i]==1) {
Ha=i;
break;
}
dfs(Ha,0);
int Ans=0;
while(L<=R) {
int mid=(L+R)>>1;
if(check(mid))Ans=mid,L=mid+1;
else R=mid-1;
}
printf("%d\n",Ans);
}
} Plist;
struct T330 {
int tot;
void dfs(const int x,const int pre,int &len,const int mid) {
multiset<int>v;
erep(i,G,x) {
int y=G.to[i];
if(y==pre)continue;
int res=0;
dfs(y,x,res,mid),res+=G.cost[i];
if(res>=mid)tot++;
else v.insert(res);
}
len=0;
while(!v.empty()) {
int res=*v.begin();
v.erase(v.begin());
set<int>::iterator it=v.lower_bound(mid-res);
if(it!=v.end())v.erase(it),tot++;
else Max(len,res);
}
}
inline void solve(void) {
int Ans=0;
while(L<=R) {
int mid=(L+R)>>1,ans=0;
tot=0,dfs(1,0,ans,mid);
if(tot>=m)Ans=mid,L=mid+1;
else R=mid-1;
}
printf("%d\n",Ans);
}
} P100;
int Ma,w;
void find(const int x,const int pre,const int s) {
if(s>Ma)Ma=s,w=x;
erep(i,G,x) {
int y=G.to[i];
if(y==pre)continue;
find(y,x,s+G.cost[i]);
}
}
bool MOP2;
inline void _main() {
n=Read(),m=Read();
L=1e9;
int flag_flower=1,flag_list=1;
ret(i,1,n) {
int a=Read(),b=Read(),c=Read();
Min(L,c),R+=c;
if(a!=1)flag_flower=0;
if(b!=a+1)flag_list=0;
deg[a]++,deg[b]++;
G.AddEdgepair(a,b,c);
}
R/=m;
find(1,-1,0),find(w,-1,0),Min(R,Ma);
if(m==1)printf("%d\n",Ma);
else if(flag_flower)Pflower.solve();
else if(flag_list)Plist.solve();
else P100.solve();
}
signed main() {
_main();
return 0;
}

