树的子结构（二叉树的创建，遍历，查询）（c++）

题目描述

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

【分析】

典型的二叉树问题。 
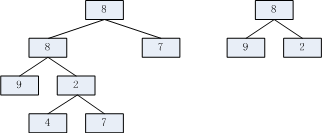
判断两个二叉树的所属关系，其实还是要从二叉树的结构特点出发，二叉树由根节点和左右孩子构成，如果一个二叉树是另一个的子树，说明这个二叉树根节点，左右孩子必然存在于另一个二叉树中，例如：

观察上图，发现第二个二叉树明显是第一个二叉树的子结构，首先，看根节点，8，第一棵树根节点为8，等于第二棵二叉树，观察其左右孩子结构，如果一致，说明所属关系成立，但是根结点为8的第一棵二叉树左孩子是8，第二棵二叉树左节点却是9，所以继续查看观察的第一棵二叉树的左子树，左子树第一个根节点就是8，所以看它的左右孩子，左孩子是9，等于第二棵二叉树，所以再看右孩子，是2，结构完全相等，说明第二棵二叉树是第一棵二叉树的子结构成立。

在判断过程中，很明显用递归方法比较简单，递归判断二叉树A的根结点和二叉树B根节点是否相同，找到相同的后，再递归判断左右孩子结构是否一致。

 

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;

struct TreeNode
{
    char val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x):val(x),left(NULL),right(NULL) {}
};

//按前序遍历输入二叉树中结点的值，构建二叉树

 void creat(TreeNode **T)
    {
        char ch;
        scanf("%c",&ch);
        if(ch=='#')
            *T=NULL;
        else
        {
            *T=(struct TreeNode *)malloc(sizeof(struct TreeNode));
            (*T)->val=ch;
            creat(&(*T)->left);
            creat(&(*T)->right);
        }
    }

//输出前序遍历
void print(TreeNode* &root)
{
    if(root==NULL)
        return;
    cout<<root->val;
    print(root->left);
    print(root->right);
}

//输出中序遍历
void print1(TreeNode* &root)
{
    if(root==NULL)
        return;
    print(root->left);
     cout<<root->val;
    print(root->right);
}

//输出后序遍历
void print2(TreeNode* &root)
{
    if(root==NULL)
        return;
    print(root->left);
    print(root->right);
    cout<<root->val;
}

class Solution
{
public:
    bool doesTree1HasTree2(TreeNode *pRoot1,TreeNode *pRoot2)
    {
        if(pRoot2==NULL)
            return true;
        if(pRoot1==NULL)
            return false;
        if(pRoot1->val!=pRoot2->val)
            return false;
        return doesTree1HasTree2(pRoot1->left,pRoot2->left)&&doesTree1HasTree2(pRoot1->right,pRoot2->right);
    }

    bool HasSubtree(TreeNode* pRoot1,TreeNode* pRoot2)
    {
        bool result=false;
        if(pRoot1!=NULL&&pRoot2!=NULL)
        {
            if(pRoot1->val==pRoot2->val)
                result=doesTree1HasTree2(pRoot1,pRoot2);
            if(!result)
                result=HasSubtree(pRoot1->left,pRoot2);
            if(!result)
                result=HasSubtree(pRoot1->right,pRoot2);
        }
        return result;
    }

};
int main()
{
    TreeNode *root1=NULL,*root2=NULL;
    creat(&root1);
    getchar();
    creat(&root2);
    //print(root1);
    //cout<<endl;
    //print(root2);

    Solution s;
   cout<<s.HasSubtree(root1,root2)<<endl;
    return 0;
}

输入：

889##24##7##7##
89##2##

输出：

1