编程内功修炼 - 算法
编程内功讲什么?
主要讲解以下算法:
分治法
堆排序
二叉树
动态规划
贪心算法
图
算法的作用:
算法解决了哪些问题?
互联网信息的访问检测,海量数据的管理
在一个交通图中,寻找最近的路
人类基因工程,dna有10万个基因,处理这些基因序列需要复杂的算法支持
上面的算法是我们没有接触到,或者是封装到底层的东西,那么作为程序员,在日常编码过程中会在什么地方使用算法呢?
在你利用代码去编写程序,去解决问题的时候,其实这些编码过程都可以总结成一个算法,只是有些算法看起来比较普遍比较一般,偶尔我们也会涉及一些复杂的算法比如一些AI.
大多数我们都会利用已有的思路(算法)去开发游戏!
注意地方:
编程内功主要讲解的是算法,并不会讲解Unity的使用
分治算法:
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。 可使用分治法求解的一些经典问题 (1)二分搜索 (2)大整数乘法 (3)Strassen矩阵乘法 (4)棋盘覆盖 (5)合并排序 (6)快速排序 (7)线性时间选择 (8)最接近点对问题 (9)循环赛日程表 (10)汉诺塔
分治算法 - 最大子数组问题:


股票问题 1,暴力求解 2,分治法
树(数据结构的一种 ):
什么是树?
![]()
1,空树 2,只有一个根节点的树 3,
什么是子树? 什么是父子结点? 什么是根节点? 什么是度?(拥有子树的个数称为结点的度)
结点关系:孩子,兄弟
什么是树的层次? 最大层是树的深度 什么是有序树和无序树?
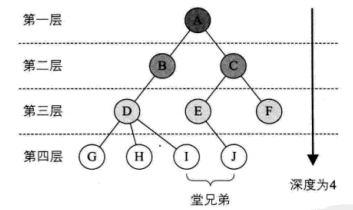
树的错误案例:
1,树只有一个根节点
2,子树之间是不相交的
3,一个结点不能有两个父结点
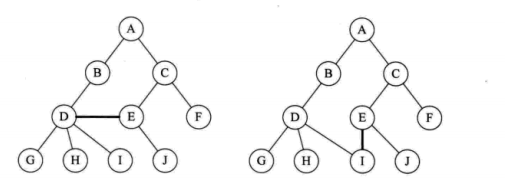
树的存储结构:
存储结构一般是 顺序存储和链式存储。
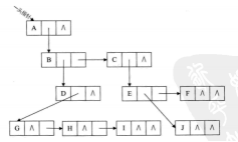
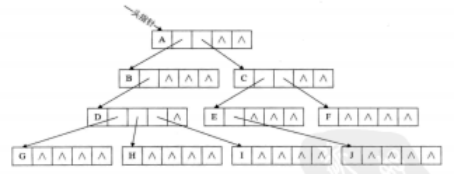
树的关系复杂 使用链式存储
1,双亲表示法

2,孩子表示法

3,孩子兄弟表示法

二叉树:
什么是二叉树?

1,空二叉树 2,只有根结点 3,大于一个结点 什么是左右子树?
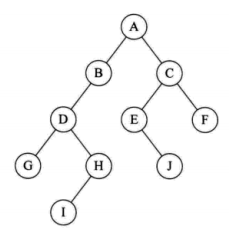
特殊二叉树:
1,斜树 左斜树 右斜树
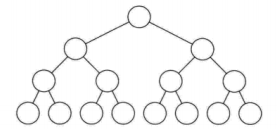
2,满二叉树
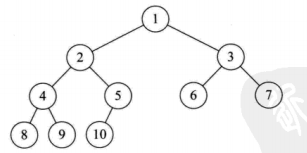
3,完全二叉树

非完全二叉树:
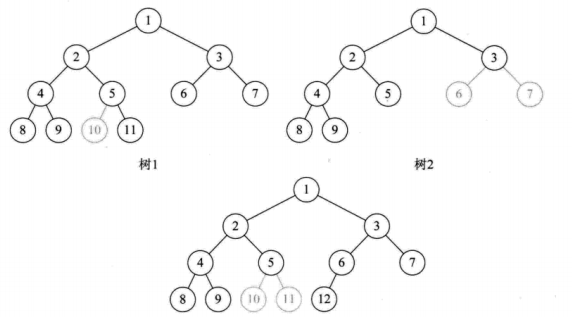
二叉树性质:
1,在二叉树的第i层上最多有 2i-1个结点(i>=1) 2,深度为k的二叉树至多有2k-1个结点 20+21+22+23+24+25+26+27+.....+2k-1+-1 =1+20+21+22+23+24+25+26+27+.....+2k-1-1 =21+21+22+23+24+25+26+27+.....+2k-1-1 =22+22+23+24+25+26+27+.....+2k-1-1 =23+23+24+25+26+27+.....+2k-1-1 =2k-1+2k-1-1 =2k-1 3,对于一个完全二叉树,假设它有n个结点,对结点进行从1开始编号,对任一结点i满足下面 a,它的双亲是结点 i/2 (除了i=1的情况) b,左孩子是 2i 右孩子是 2i+1 c,如果2i>n 说明无左孩子 2i+1>n 说明无右孩子
二叉树存储结构:
一般的树来说是一对多的关系,使用顺序结构存储起来比较困难,但是二叉树是一种特殊的树,每个结点最多有两个子节点,并且子节点有左右之分,并且兄弟,父亲,孩子可以很方便的通过编号得到,所以我们使用顺序存储结构使用二叉树的存储。
二叉树存储 - 1:


二叉树存储 - 2:
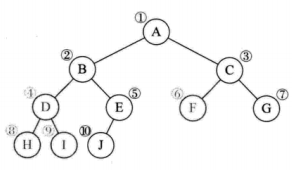

二叉树存储 - 3:
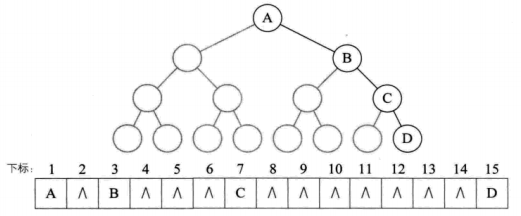
顺序存储一般只用于完全二叉树
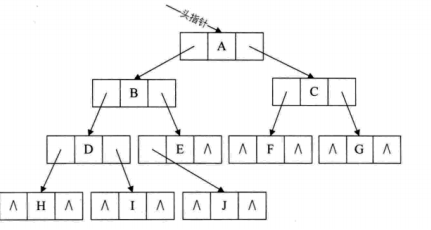
二叉树 - 二叉链表存储:
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域,我们称这样的链表为二叉链表。

二叉树的遍历:
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次且仅被访问一次。 1,前序遍历 先输出当前结点的数据,再依次遍历输出左结点和右结点 A (B) (C) B (D) C (E) F D G H E I A B D G H C E I

2,中序遍历 先遍历输出左结点,再输出当前结点的数据,再遍历输出右结点 GDH B A E I C F

3,后序遍历 先遍历输出左结点,再遍历输出右结点,最后输出当前结点的数据 G H D B I E F C A
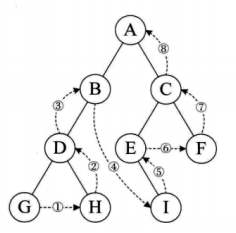
4,层序遍历 从树的第一层开始,从上到下逐层遍历,在同一层中,从左到右对结点 逐个访问输出
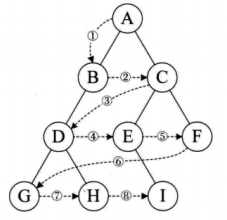

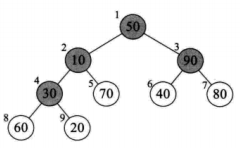
二叉排序树:
二叉排序树,又称为二叉查找树。它或者是一棵空树,或者是具有下列性质的二叉树。 若它的左子树不为空,则左子树上所有的结点的值均小于根结构的值; 若它的右子树不为空,则右字数上所有结点的值均大于它的根结点的值; 它的左右子树也分别为二叉排序树。 1,排序方便 2,方便查找 3,方便插入和删除
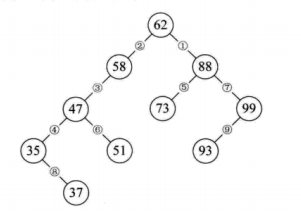
二叉排序树 删除操作:
二叉排序树
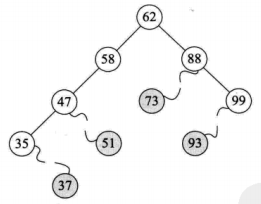
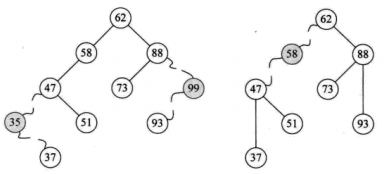
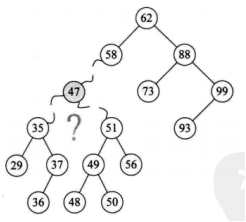
二叉排序树删除
1,叶子结点
2,仅有左子树或者右子数的结点
3,左右子树都有
二叉排序树的存储:
因为二叉排序树的存储,跟自身值的大小有关系,并不是想之前学习的完全二叉树使用顺序结构可以存储的 所以我们使用链式结构存储二叉排序树。
一个是树类的定义 BSTree
一个是结点类的定义BSNode
堆:
堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于等于其左右孩子结点的值,称为小顶堆!
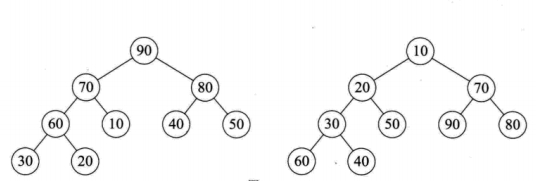
堆排序:
堆排序算法就是利用堆(小顶堆或者大顶堆)进行排序的方法。 将待排序的序列构造成一个大顶堆,此时整个序列的最大值就是根节点。将它移走(跟堆的最后一个元素交换,此时末尾元素就是最大值),然后将剩余的n-1个序列重新构造成一个堆,这样就会得到n个元素中的次小值。如此反复执行,便能得到一个有序序列了。
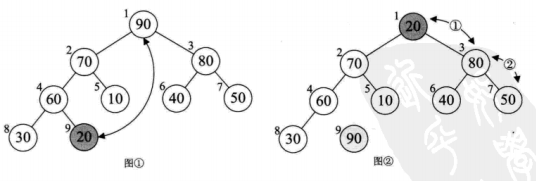
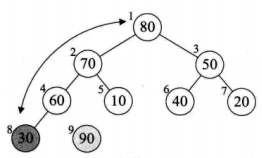
堆排序:
动态规划(Dynamic Programming):
什么是动态规划,我们要如何描述它?
动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。
动态规划和分治法相似,都是通过组合子问题的解来求解原问题。分治法将问题划分成互不相交的子问题,递归求解子问题,再将他们的解组合起来,求出原问题的解。与之相反,动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。在这种情况下,分治算法会做出许多不必要的工作,它会反复的求解那些公共子问题。而动态规划算法对每个子子问题只求解一次,将结果保存到表格中,从而无需每次求解一个子子问题都要重新计算。
动态规划 - 钢条切割问题:
假定我们知道sering公司出售一段长度为I英寸的钢条的价格为pi(i=1,2,3….)钢条长度为整英寸如图给出价格表的描述(任意长度的钢条价格都有)
先给我们一段长度为n的钢条,问怎么切割,获得的收益最大 rn? 考虑n=4的时候
假如一个最优解把n段七个成了k段(1<=k<=n),那么最优切割方案:
最大收益:
![]()

第一种求最优解方案: 对于 r n (n>=1),最优切割收益:
将切割方案分成下面几种 1,不切割 收益为pn 2,将它切割成两半,切割成两半的情况有,对每种情况求最优解 (1,n-1) (2,n-2) (3,n-3) (4,n-4) ..... (n-1,1) 对这两半分别求最优解,最优解的和就是当前情况的最优解 第二种求最优解方案: 我们从钢条的左边切下长度为i的一段,只对右边剩下长度为n-i的一段继续进行切割,对左边的不再切割。这样,不做任何切割的方案就是:当第一段长度为n的时候,收益为pn,剩余长度为0,对应的收益为0。如果第一段长度为i,收益为pi:
代码实现 - 自顶向下递归实现 分析效率,关于上述方法的运行性能时间问题。 动态规划的方法进行求解 上面的方法之所以效率很低,是因为它反复求解相同的子问题。因此,动态规划算法安排求解的顺序,对每个子问题只求解一次,并将结果保存下来。如果随后再次需要此子问题的解,只需查找保存的结果,不必重新计算。因此动态规划的方法是付出额外的内存空间来节省计算时间。 动态规划有两种等价的实现方法(我们使用上面的钢条切割问题为例,实现这两种方法) 第一种方法是 带备忘的自顶向下法 此方法依然是按照自然的递归形式编写过程,但过程中会保存每个子问题的解(通常保存在一个数组中)。当需要计算一个子问题的解时,过程首先检查是否已经保存过此解。如果是,则直接返回保存的值,从而节省了计算时间;如果没有保存过此解,按照正常方式计算这个子问题。我们称这个递归过程是带备忘的。 第二种方法是 自底向上法 首先恰当的定义子问题的规模,使得任何问题的求解都只依赖于更小的子问题的解。因而我们将子问题按照规模排序,按从小到大的顺序求解。当求解某个问题的时候,它所依赖的更小的子问题都已经求解完毕,结果已经保存。
动态规划 - 01背包问题:
问题描述: 假设现有容量m kg的背包,另外有i个物品,重量分别为w[1] w[2] ... w[i] (kg),价值分别为p[1] p[2] ... p[i] (元),将哪些物品放入背包可以使得背包的总价值最大?最大价值是多少? (示例一:m=10 i=3 重量和价值分别为 3kg-4元 4kg-5元 5kg-6元 ) 1,穷举法(把所有情况列出来,比较得到 总价值最大的情况) 如果容量增大,物品增多,这个方法的运行时间将成指数增长 2,动态规划算法 我们要求得i个物体放入容量为m(kg)的背包的最大价值(记为 c[i,m])。在选择物品的时候,对于每种物品i只有两种选择,即装入背包或不装入背包。某种物品不能装入多次(可以认为每种物品只有一个),因此该问题被称为0-1背包问题 对于c[i,m]有下面几种情况: a、c[i,0]=c[0,m]=0 b、c[i,m]=c[i-1,m] w[i]>m(最后一个物品的重量大于容量,直接舍弃不用) w[i]<=m的时候有两种情况,一种是放入i,一种是不放入i 不放入i c[i,m]=c[i-1,m] 放入i c[i,m]=c[i-1,m-w[i]]+p[i] c[i,m]=max(不放入i,放入i)
贪心算法:
对于许多最优化问题,使用动态规划算法来求最优解有些杀鸡用牛刀了,可以使用更加简单、更加高效的算法。贪心算法就是这样的算法,它在每一步做出当时看起来最佳的选择。也就是说它总是做出局部最优的选择,从而得到全局最优解。
对于某些问题并不保证得到最0优解,但对很多问题确实可以求得最优解。
贪心算法 - 活动选择问题:
有n个需要在同一天使用同一个教室的活动a1,a2,…,an,教室同一时刻只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,ai和aj两个活动就可以被安排在这一天。该问题就是要安排这些活动使得尽量多的活动能不冲突的举行(最大兼容活动子集)。例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。
{a3,a9,a11}是一个兼容的活动子集,但它不是最大子集,因为子集{a1,a4,a8,a11}更大,实际上它是我们这个问题的最大兼容子集,但它不是唯一的一个{a2,a4,a9,a11}
![]()
1,动态规划算法解决思路 我们使用Sij代表在活动ai结束之后,且在aj开始之前的那些活动的集合,我们使用c[i,j]代表Sij的最大兼容活动子集的大小,对于上述问题就是求c[0,12]的解 a, 当i>=j-1或者Sij 中没有任何活动元素的时候, c[i,j]=0 b,当i<j-1 1,Sij不存在活动,c[i,j]=0 2,Sij存在活动的时候,c[i,j]= max{c[i,k]+c[k,j]+1} ak属于Sij,这里是遍历Sij的集合,然后求得最大兼容子集 2,贪心算法 想要使用贪心算法的话,得先找到适合贪心算法的规律(局部最优选择) 对于任何非空的活动集合S,假如am是S中结束时间最早的活动,则am一定在S的某个最大兼容活动子集中。 (如何证明上面的结论?反证法) 递归解决 迭代解决
贪心算法 - 钱币找零问题:
这个问题在我们的日常生活中就更加普遍了。假设1元、2元、5元、10元、20元、50元、100元的纸币分别有c0, c1, c2, c3, c4, c5, c6张。现在要用这些钱来支付K元,至少要用多少张纸币?用贪心算法的思想,很显然,每一步尽可能用面值大的纸币即可。
int Count[N]={3,0,2,1,0,3,5};
int Value[N]={1,2,5,10,20,50,100};












 浙公网安备 33010602011771号
浙公网安备 33010602011771号