栈和队列
栈和队列:
栈和队列是非常重要的两种数据结构,在软件设计中应用很多。栈和队列也是线性结构,线性表、栈和队列这三种数据结构的数据元素以及数据元素间的逻辑关系完全相同,差别是线性表的操作不受限制,而栈和队列的操作受到限制。栈的操作只能在表的一端进行,队列的插入操作在表的一端进行而其它操作在表的另一端进行,所以,把栈和队列称为操作受限的线性表。
栈:
栈(Stack)是操作限定在表的尾端进行的线性表。表尾由于要进行插入、删除等操作,所以,它具有特殊的含义,把表尾称为栈顶( Top),另一端是固定的,叫栈底( Bottom)。当栈中没有数据元素时叫空栈(Empty Stack)。 栈通常记为: S= (a1,a2,…,an),S是英文单词stack的第 1 个字母。a1为栈底元素,an为栈顶元素。这n个数据元素按照a1,a2,…,an的顺序依次入栈,而出栈的次序相反,an第一个出栈,a1最后一个出栈。所以,栈的操作是按照后进先出(Last In First Out,简称LIFO)或先进后出(First In Last Out,简称FILO)的原则进行的,因此,栈又称为LIFO表或FILO表。栈的操作示意图如图所示。
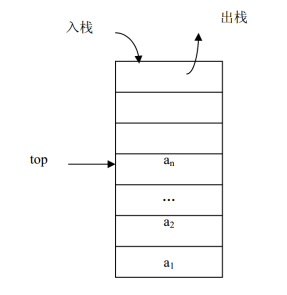
BCL中的栈:
C#2.0 一下版本只提供了非泛型的Stack类(存储object类型) C#2.0 提供了泛型的Stack<T>类 重要的方法如下 1,Push()入栈(添加数据) 2,Pop()出栈(删除数据,返回被删除的数据) 3,Peek()取得栈顶的数据,不删除 4,Clear()清空所有数据 4,Count取得栈中数据的个数
栈的接口定义:
public interface IStack<T> { int Count{get;} int GetLength(); //求栈的长度 bool IsEmpty(); //判断栈是否为空 void Clear(); //清空操作 void Push(T item); //入栈操作 T Pop(); //出栈操作 T Peek(); //取栈顶元素 }
栈的存储和代码实现-1.1,顺序栈:
用一片连续的存储空间来存储栈中的数据元素(使用数组),这样的栈称为顺序栈(Sequence Stack)。类似于顺序表,用一维数组来存放顺序栈中的数据元素。栈顶指示器 top 设在数组下标为 0 的端, top 随着插入和删除而变化,当栈为空时,top=-1。下图是顺序栈的栈顶指示器 top 与栈中数据元素的关系图。
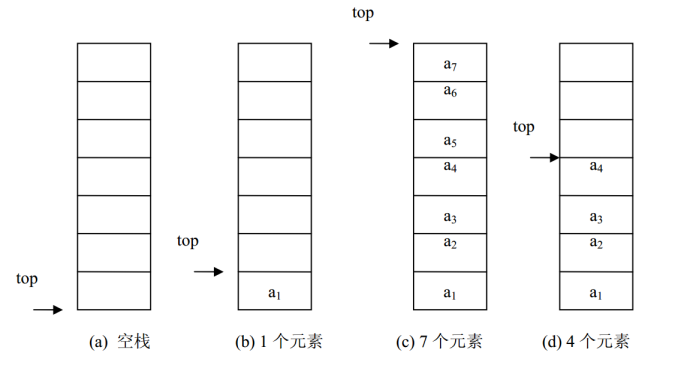
栈的存储和代码实现-1.2,顺序栈:
class SeqStack<T>:IStack<T> { private T[] data; private int top; public SeqStack(int size) { data = new T[size]; top = -1; } //默认构造数组的最大容量为10 public SeqStack():this(10) { } public int GetLength() { return top + 1; } public int Count { get { return GetLength(); } } public bool IsEmpty() { return top <= -1; } public void Clear() { top = -1; Array.Clear(data,0,data.Length); } public void Push(T item) { data[top + 1] = item; top++; } /// <summary> /// 出栈 /// </summary> /// <returns></returns> public T Pop() { T temp = data[top]; top--; return temp; } public T Peek() { return data[top]; } }
栈的存储和代码实现-2.1,链栈:
栈的另外一种存储方式是链式存储,这样的栈称为链栈(Linked Stack)。链栈通常用单链表来表示,它的实现是单链表的简化。所以,链栈结点的结构与单链表结点的结构一样,如图 3.3 所示。由于链栈的操作只是在一端进行,为了操作方便,把栈顶设在链表的头部,并且不需要头结点。
2.2,链栈-链栈结点实现:
public class Node<T> { private T data; //数据域 private Node<T> next; //引用域 //构造器 public Node(T val, Node<T> p) { data = val; next = p; } //构造器 public Node(Node<T> p) { next = p; } //构造器 public Node(T val) { data = val; next = null; } //构造器 public Node() { data = default(T); next = null; } //数据域属 public T Data { get { return data; } set { data = value; } } //引用域属性 public Node<T> Next { get { return next; } set { next = value; } } }
2.3,链栈-代码实现:

把链栈看作一个泛型类,类名为 LinkStack<T>。 LinkStack<T>类中有一个字段 top 表示栈顶指示器。由于栈只能访问栈顶的数据元素,而链栈的栈顶指示器又不能指示栈的数据元素的个数。所以,求链栈的长度时,必须把栈中的数据元素一个个出栈,每出栈一个数据元素,计数器就增加 1,但这样会破坏栈的结构。为保留栈中的数据元素,需把出栈的数据元素先压入另外一个栈,计算完长度后,再把数据元素压入原来的栈。但这种算法的空间复杂度和时间复杂度都很高,所以,以上两种算法都不是理想的解决方法。理想的解决方法是 LinkStack<T>类增设一个字段 num 表示链栈中结点的个数。
队列:
队列(Queue)是插入操作限定在表的尾部而其它操作限定在表的头部进行的线性表。把进行插入操作的表尾称为队尾(Rear),把进行其它操作的头部称为队头(Front)。当队列中没有数据元素时称为空队列(Empty Queue)。 队列通常记为: Q= (a1,a2,…,an),Q是英文单词queue的第 1 个字母。a1为队头元素,an为队尾元素。这n个元素是按照a1,a2,…,an的次序依次入队的,出对的次序与入队相同,a1第一个出队,an最后一个出队。所以,对列的操作是按照先进先出(First In First Out)或后进后出( Last In Last Out)的原则进行的,因此,队列又称为FIFO表或LILO表。队列Q的操作示意图如图所示。 在实际生活中有许多类似于队列的例子。比如,排队取钱,先来的先取,后来的排在队尾。 队列的操作是线性表操作的一个子集。队列的操作主要包括在队尾插入元素、在队头删除元素、取队头元素和判断队列是否为空等。与栈一样,队列的运算是定义在逻辑结构层次上的,而运算的具体实现是建立在物理存储结构层次上的。因此,把队列的操作作为逻辑结构的一部分,每个操作的具体实现只有在确定了队列的存储结构之后才能完成。队列的基本运算不 是它的全部运算,而是一些常用的基本运算。
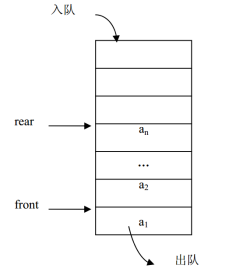
BCL 中的队列:
C#2.0 以下版本提供了非泛型的Queue类 C#2.0 提供了泛型Queue<T>类 方法 1,Enqueue()入队(放在队尾) 2,Dequeue()出队(移除队首元素,并返回被移除的元素) 3,Peek()取得队首的元素,不移除 4,Clear()清空元素 属性 5,Count获取队列中元素的个数
队列接口定义:
public interface IQueue<T> { int Count{get;}//取得队列长度的属性 int GetLength(); //求队列的长度 bool IsEmpty(); //判断对列是否为空 void Clear(); //清空队列 void Enqueue(T item); //入队 T Dequque(); //出队 T Peek(); //取队头元素 }
1.1 顺序队列:
用一片连续的存储空间来存储队列中的数据元素,这样的队列称为顺序队列(Sequence Queue)。类似于顺序栈,用一维数组来存放顺序队列中的数据元素。队头位置设在数组下标为 0 的端,用 front 表示;队尾位置设在数组的另一端,用 rear 表示。 front 和 rear 随着插入和删除而变化。当队列为空时, front=rear=-1。
图是顺序队列的两个指示器与队列中数据元素的关系图。
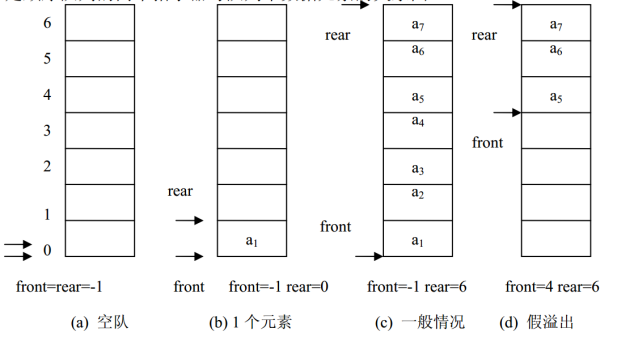
1.2 顺序队列-(循环顺序队列):
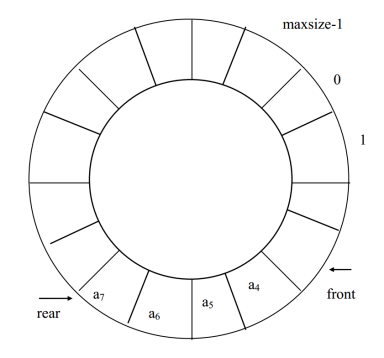
如果再有一个数据元素入队就会出现溢出。但事实上队列中并未满,还有空闲空间,把这种现象称为“假溢出”。这是由于队列“队尾入队头出”的操作原则造成的。解决假溢出的方法是将顺序队列看成是首尾相接的循环结构,头尾指示器的关系不变,这种队列叫循环顺序队列(Circular sequence Queue)。循环队列如图所示。
1.3 顺序队列-代码实现:
把循环顺序队列看作是一个泛型类,类名叫 CSeqStack<T>,“ C”是英文单词 circular 的第 1 个字母。 CSeqStack<T>类实现了接口 IQueue<T>。用数组来存储循环顺序队列中的元素,在 CSeqStack<T>类中用字段 data 来表示。用字段maxsize 表示循环顺序队列的容量, maxsize 的值可以根据实际需要修改,这通过CSeqStack<T>类的构造器中的参数 size 来实现,循环顺序队列中的元素由 data[0]开始依次顺序存放。字段 front 表示队头, front 的范围是 0 到 maxsize-1。字段 rear表示队尾,rear 的范围也是 0 到 maxsize-1。如果循环顺序队列为空,front=rear=-1。当执行入队列操作时需要判断循环顺序队列是否已满,如果循环顺序队列已满,(rear + 1) % maxsize==front , 循 环 顺 序 队 列 已 满 不 能 插 入 元 素 。 所 以 ,CSeqStack<T>类除了要实现接口 IQueue<T>中的方法外,还需要实现判断循环顺序队列是否已满的成员方法。
2.1链队列:
队列的另外一种存储方式是链式存储,这样的队列称为链队列(Linked Queue)。同链栈一样,链队列通常用单链表来表示,它的实现是单链表的简化。所以,链队列的结点的结构与单链表一样,如图所示。由于链队列的操作只是在一端进行,为了操作方便,把队头设在链表的头部,并且不需要头结点。
2.2链队列-链队列结点类:

public class Node<T> { private T data; //数据域 private Node<T> next; //引用域 //构造器 public Node(T val, Node<T> p) { data = val; next = p; } //构造器 public Node(Node<T> p) { next = p; } //构造器 public Node(T val) { data = val; next = null; } //构造器 public Node() { data = default(T); next = null; } //数据域属性 public T Data { get { return data; } set { data = value; } } //引用域属性 public Node<T> Next { get { return next; } set { next = value; } } }
2.3链队列-代码实现:
把链队列看作一个泛型类,类名为 LinkQueue<T>。 LinkQueue<T>类中有两个字段 front 和 rear,表示队头指示器和队尾指示器。由于队列只能访问队头的数据元素,而链队列的队头指示器和队尾指示器又不能指示队列的元素个数,所以,与链栈一样,在 LinkQueue<T>类增设一个字段 num 表示链队列中结点的个数。
栈和队列的应用举例:
编程判断一个字符串是否是回文。回文是指一个字符序列以中间字符为基准两边字符完全相同,如字符序列“ ACBDEDBCA”是回文。
算法思想:判断一个字符序列是否是回文,就是把第一个字符与最后一个字符相比较,第二个字符与倒数第二个字符比较,依次类推,第 i 个字符与第 n-i个字符比较。如果每次比较都相等,则为回文,如果某次比较不相等,就不是回文。因此,可以把字符序列分别入队列和栈,然后逐个出队列和出栈并比较出队列的字符和出栈的字符是否相等,若全部相等则该字符序列就是回文,否则就不是回文。



