(转载)初识小波变换——傅里叶变换的局限性
原文链接:https://www.cnblogs.com/jfdwd/p/9249850.html
https://blog.csdn.net/m0_37269455/article/details/74201023
这原是“逼乎”上的一遍问答,我也在博客网站上看到了同样的转载博文,可是由于图片转载不过来影响了阅读,我在这里重新把图像转载到了CSDN,并且不是完全照搬原文,而是增加了一些其他的东西进去,供大家阅读。感谢原作者!
从傅里叶变换到小波变换,并不是一个完全抽象的东西,可以讲得很形象。小波变换有着明确的物理意义,如果我们从它的提出时所面对的问题看起,可以整理出非常清晰的思路。
下面我就按照傅里叶-->短时傅里叶变换-->小波变换的顺序,讲一下为什么会出现小波这个东西、小波究竟是怎样的思路。
小波,一个神奇的波,当去学习小波的时候,第一个首先要做的就是回顾傅立叶变换(又回来了),因为他们都是频率变换的方法,而傅立叶变换是最入门的,也是最先了解的,通过傅立叶变换,了解缺点,改进,慢慢的就成了小波变换。主要的关键的方向是傅立叶变换、短时傅立叶变换,小波变换等,第二代小波的什么的就不说了,太多了没太多意义。当然,其中会看到很多的名词,例如,内积,基,归一化正交,投影,Hilbert空间,多分辨率,父小波,母小波,这些不同的名词也是学习小波路上的标志牌,所以在刚学习小波变换的时候,看着三个方向和标志牌,可以顺利的走下去,当然路上的美景要自己去欣赏(这里的美景就是定义和推导了)。因为内容太多,不是很重要的地方我都注释为(查定义)一堆文字的就是理论(可以大体一看不用立刻就懂)。
一、基
傅立叶变换和小波变换,都会听到分解和重构,其中这个就是根本,因为他们的变化都是将信号看成由若干个东西组成的,而且这些东西能够处理还原成比原来更好的信号。那怎么分解呢?那就需要一个分解的量,也就是常说的基,基的了解可以类比向量,向量空间的一个向量可以分解在x,y方向,同时在各个方向定义单位向量\(e_1\)、\(e_2\),这样任意一个向量都可以表示为\(a=xe_1+ye_2\),这个是二维空间的基,

而对于傅立叶变换的基是不同频率的正弦曲线,所以傅立叶变换是把信号波分解成不同频率的正弦波的叠加和,而对于小波变换就是把一个信号分解成一系列的小波,这里时候,也许就会问,小波变换的小波是什么啊,定义中就是告诉我们小波,因为这个小波实在是太多,一个是种类多,还有就是同一种小波还可以尺度变换,但是小波在整个时间范围的幅度*均值是0,具有有限的持续时间和突变的频率和振幅,可以是不规则,也可以是不对称,很明显正弦波就不是小波,什么的是呢,看下面几个图就是
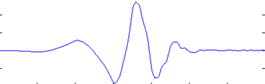
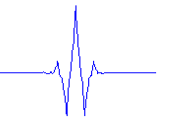
当有了基,以后有什么用呢?
下面看一个傅立叶变换的实例:
对于一个信号的表达式为\(x=sin(2πt)+0.5sin(2π*5t)\);
这里可以看到是他的基就是sin函数,频率是1和5,下面看看图形的表示,是不是感受了到了频域变换给人的一目了然。

基具有非冗余性,即使基不是正交的,有相关性,但若去掉其中任何一个,则不成为基,这一点也叫完备性;基的表示有唯一性,即给定一族基对一个函数的表达是唯一的;一般情况下基非正交,也称为为exact frame(Resize basis),这个时候要表示信号可以将基正交化成唯一的正交基(对偶为其自身);也可以求其对偶框架(dual frame),其对应了小波变换中的双正交情形!信号可以依框架分解,然后用对偶框架重构。若在基集里添加一些新的向量,并随意调整空间位置,则有可能成为框架。把函数与基或框架作内积,也可以说成是一种函数空间到系数空间的变换。若某种变换后的能量(内积的*方和度量)仍然有一个大于0的上下界,才可以成为框架,由于框架的冗余性,所以系数的表达也不具有唯一性。若上下界相等,则为紧框架,且界表示冗余度。若上下界相等为且为1,称为pasval identity frame,此时不一定为正交基(想象把一组正交基中某一个拆成两个同方向的基之和,则pasval identity仍然成立),此时若加上基的长度均为一的条件,则框架退化为正交基。可能你会问我们用基来表示信号就行了啊,为什么还要框架呢?其实很多信号表示方法不能构成基,却能构成框架,如短时傅立叶变换中如要求窗函数满足基条件,则可推出该函数有很差的时频局部化性质(事实上退化为了傅立叶变换。
二、内积
在Hilbert(希尔伯特)空间(查定义)里看到这个东西,用来刻画两个向量的夹角,当内积为0时,两个向量正交,若g为Hilbert空间里的正交基的时候,内积为f向基上的正交投影;(Hilbert空间是一个很直观的空间,我一直都理解为欧氏空间去理解定义在其上的东西,\(L^2\)(*方可积,查定义)和\(l^2\)同样为Hilbert空间。
下面这个公式是基本,经过变形后会用在推导中:

如果两个向量的内积为0 ,就说他们是正交的。
如果一个向量序列相互对偶正交,并且长度都为1,那么就说他们是正交归一化的。
对于\(f(t)⊆L^2(R)\),存在\(L^2(R)\);上一组标准正交基\(g_i(t),i=1,2,3….\),使得

\(L^2(R)\)上任意一个函数\(f(t)\)都可以由\(L^2(R)\)上的一个规范正交基\(g_i(t)\)进行线性组合表示出来
三、傅里叶变换的缺点
先列举出来缺点,然后再说明:
(1)Fourier分析不能刻画时间域上信号的局部特性
(2)Fourier分析对突变和非*稳信号的效果不好,没有时频分析
傅立叶变换傅立叶变换将函数投影到三角波上,将函数分解成了不同频率的三角波,这不能不说是一个伟大的发现,但是在大量的应用中,傅立叶变换的局限性却日趋明显,事实上在光滑*稳信号的表示中,傅立叶基已经达到了*似最优表示,但是日常生活中的信号却并不是一直光滑的,而且奇异是*凡的,傅立叶在奇异点的表现就着实让人不爽,从对方波的傅立叶逼*就可以看出来,用了大量不同频率的三角波去逼*其系数衰减程度相当缓慢,而且会产生Gibbs(吉布斯)效应。其内在的原因是其基为全局性基,没有局部化能力,以至局部一个小小的摆动也会影响全局的系数。实际应用中很需要时频局部化,傅立叶显然缺乏此能力了。即使如此,由于其鲜明的物理意义和快速计算,在很多场合仍然应用广泛。傅立叶变换在从连续到离散的情形是值得借鉴与学习的,大家都知道,时间周期对应频域离散,时间离散对应频域周期,时间离散周期对应频域离散 周期,DFT其实是将离散信号做周期延拓然后做傅立叶变换再截取一个周期,反变换同样如此,所以DFT用的是块基的概念,这样如果信号两端的信号连接后不再光滑(即使两边都光滑),同样会在边界上产生大幅值系数(边界效应),延伸到图像中就是块效应。当对信号做对称周期延拓后再做傅立叶变换得到的正弦系数全部为0,也就是任何对称函数可以写成余弦的线性组合,同样按照离散的思路构造得到的是离散块余弦基,即DCT变换,虽然DCT可以通过对称后周期延拓再变换减少了边界效应(两边信号接上了,但不一定*滑),但任不能消除块效应,尤其是图像变换中人为将图像分成8*8处理后块效应更加明显。但是DCT很好的能量聚集效应让人惊奇,加之快速计算方法使它替代DFT成为图像的压缩的标准了很长时间(JPEG)。
上面一堆文字也许看的有点蒙,还是用图来说明
第一个就是傅立叶变换是整个时域,所以没有局部特征,这个也是他的基函数决定的看图,同时如果在时域张有了突变,那么在频域就需要大量的三角波去拟合,这也是傅立叶变换性质决定的。
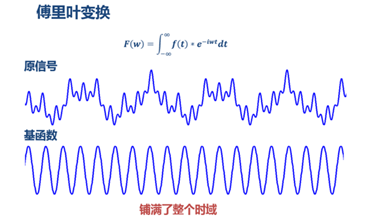
第二个就是面对非*稳信号,傅立叶变换可以看到由哪些频域组成,但是不知道各成分对应的时刻是什么,也就是没有时频分析,看不出来信号频域随着时间变换的情况,反过来说就是,一个的频图对应好几个时域图,不知道是哪个,这个在实际应用中就不好了,看图

做FFT后,我们发现这三个时域上有巨大差异的信号,频谱(幅值谱)却非常一致。尤其是下边两个非*稳信号,我们从频谱上无法区分它们,因为它们包含的四个频率的信号的成分确实是一样的,只是出现的先后顺序不同。
可见,傅里叶变换处理非*稳信号有天生缺陷。它只能获取一段信号总体上包含哪些频率的成分,但是对各成分出现的时刻并无所知。因此时域相差很大的两个信号,可能频谱图一样。
然而*稳信号大多是人为制造出来的,自然界的大量信号几乎都是非*稳的,所以在比如生物医学信号分析等领域的论文中,基本看不到单纯傅里叶变换这样naive的方法。

上图所示的是一个正常人的事件相关电位。对于这样的非*稳信号,只知道包含哪些频率成分是不够的,我们还想知道各个成分出现的时间。知道信号频率随时间变化的情况,各个时刻的瞬时频率及其幅值——这也就是时频分析。
四、短时傅里叶变换(Short-time Fourier Transform,STFT)
有了缺点就要改进了,这里就出来了短时傅立叶变换,也叫加窗傅立叶变换,顾名思义,就是因为傅立叶变换的时域太长了,所以要弄短一点,这样就有了局部性。
定义:把整个时域过程分解成无数个等长的小过程,每个小过程*似*稳,再傅里叶变换,就知道在哪个时间点上出现了什么频率了。这就是短时傅里叶变换。下面就是示意图

时域上分成一段一段做FFT,不就知道频率成分随着时间的变化情况了吗!
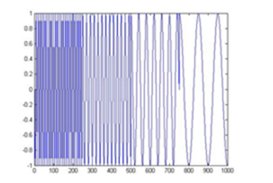
可能理解这一点最好的方式是举例子。首先,因为我们的变换是对时间和频率的函数(不像傅立叶变换,仅仅是对频率的函数),它是二维的(如果加上幅度则是三维)。以下图所示的非*稳信号为例:

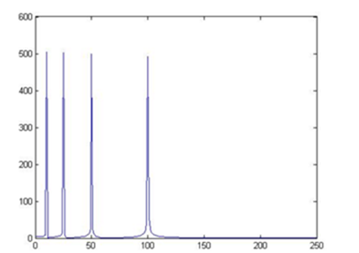
在这个信号中,在不同时刻有四个频率分量。0-250ms内信号的频率为300Hz,其余每个250ms的间隔的信号频率分别为200Hz,100Hz和50Hz。很明显,这是一个非*稳信号,让我们看一看它的短时傅立叶变换:用这样的方法,可以得到一个信号的时频图了:

图上既能看到10Hz, 25 Hz, 50 Hz, 100 Hz四个频域成分,还能看到出现的时间。两排峰是对称的,所以大家只用看一排就行了。
看着貌似解决了问题,好像有了局部性,但是这个名字叫做加窗傅立叶变换,那么这个窗要多大了呢?
窗太窄,窗内的信号太短,会导致频率分析不够精准,频率分辨率差。
窗太宽,时域上又不够精细,时间分辨率低。


(这里插一句,这个道理可以用海森堡不确定性原理来解释。类似于我们不能同时获取一个粒子的动量和位置,我们也不能同时获取信号绝对精准的时刻和频率。这也是一对鱼和熊掌,不可兼得的矛盾体。我们不知道在某个瞬间哪个频率分量存在,我们知道的只能是在一个时间段内某个频带的分量存在。所以绝对意义的瞬时频率是不存在的。)
上图对同一个信号(4个频率成分)采用不同宽度的窗做STFT,结果如右图。用窄窗,时频图在时间轴上分辨率很高,几个峰基本成矩形,而用宽窗则变成了绵延的矮山。但是频率轴上,窄窗明显不如下边两个宽窗精确。



所以窄窗口时间分辨率高、频率分辨率低,宽窗口时间分辨率低、频率分辨率高。
对于时变的非稳态信号,高频适合小窗口,低频适合大窗口。然而STFT的窗口是固定的,在一次STFT中宽度不会变化,所以STFT还是无法满足非稳态信号变化的频率的需求。
五、小波变换
真是千呼万唤始出来了,终于看见小波了啊。
这里先引入小波,回顾一下基,然后再看看小波的优点,其实就是上面傅立叶缺点的解决。
对于加窗傅立叶变换让人头疼的就是窗口的大小问题,如果我们让窗口的大小可以改变,不就完美了吗?答案是肯定的,小波就是基于这个思路,但是不同的是。STFT是给信号加窗,分段做FFT;而小波变换并没有采用窗的思想,更没有做傅里叶变换。小波直接把傅里叶变换的基给换了——将无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率,还可以定位到时间了~
这里就又回到了最开始的基了。
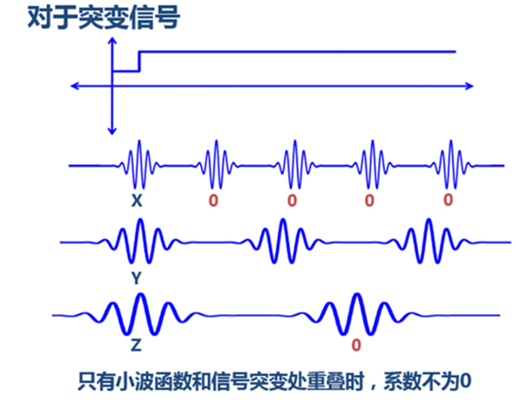
这个基函数会伸缩、会*移(其实是两个正交基的分解)。缩得窄,对应高频;伸得宽,对应低频。然后这个基函数不断和信号做相乘。某一个尺度(宽窄)下乘出来的结果,就可以理解成信号所包含的当前尺度对应频率成分有多少。于是,基函数会在某些尺度下,与信号相乘得到一个很大的值,因为此时二者有一种重合关系。那么我们就知道信号包含该频率的成分的多少。如前边所说,小波做的改变就在于,将无限长的三角函数基换成了有限长的会衰减的小波基。效果如下图

现在来看一下小波公式

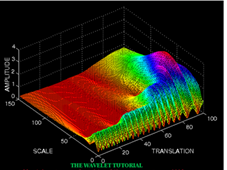
从公式可以看出,不同于傅里叶变换,变量只有频率ω,小波变换有两个变量:尺度a(scale)和*移量 τ(translation)。尺度a控制小波函数的伸缩,*移量τ控制小波函数的*移。尺度就对应于频率(反比),*移量 τ就对应于时间。如下图

当伸缩、*移到这么一种重合情况时,也会相乘得到一个大的值。这时候和傅里叶变换不同的是,这不仅可以知道信号有这样频率的成分,而且知道它在时域上存在的具体位置。
而当我们在每个尺度下都*移着和信号乘过一遍后,我们就知道信号在每个位置都包含哪些频率成分。
看到了吗?有了小波,我们从此再也不害怕非稳定信号啦!从此可以做时频分析啦!
(1) 解决了局部性

(2)解决时频分析
做傅里叶变换只能得到一个频谱,做小波变换却可以得到一个时频谱!
知识原理补充:
1.关于海森堡不确定性原理(测不准原理)
不确定性原理,或者叫测不准原理,最早出自量子力学,意为在微观世界,粒子的位置与动量不可同时被确定。但是这个原理并不局限于量子力学,有很多物理量都有这样的特征,比如能量和时间、角动量和角度。体现在信号领域就是时域和频域。不过更准确一点的表述应该是:一个信号不能在时空域和频域上同时过于集中;一个函数时域越“窄”,它经傅里叶变换的频域后就越“宽”。
如果有兴趣深入研究一下的话,这个原理其实非常耐人寻味。信号处理中的一些新理论在根本上也和它有所相连,比如压缩感知。如果你剥开它复杂的数学描述,最后会发现它在本质上能实现其实和不确定性原理密切相关。而且大家不觉得这样一些矛盾的东西在哲学意义上也很奇妙吗?
2.关于正交化
什么是正交化?为什么说小波能实现正交化是优势?
简单说,如果采用正交基,变换域系数会没有冗余信息,变换前后的信号能量相等,等于是用最少的数据表达最大的信息量,利于数值压缩等领域。JPEG2000压缩就是用正交小波变换。
比如典型的正交基:二维笛卡尔坐标系的(1,0)、(0,1),用它们表达一个信号显然非常高效,计算简单。而如果用三个互成120°的向量表达,则会有信息冗余,有重复表达。
但是并不意味着正交一定优于不正交。比如如果是做图像增强,有时候反而希望能有一些冗余信息,更利于对噪声的抑制和对某些特征的增强。
3.关于瞬时频率
原问题:图中时刻点对应一频率值,一个时刻点只有一个信号值,又怎么能得到他的频率呢?
很好的问题。如文中所说,绝对意义的瞬时频率其实是不存在的。单看一个时刻点的一个信号值,当然得不到它的频率。我们只不过是用很短的一段信号的频率作为该时刻的频率,所以我们得到的只是时间分辨率有限的*似分析结果。这一想法在STFT上体现得很明显。小波用衰减的基函数去测定信号的瞬时频率,思想也类似。(不过到了Hilbert变换,思路就不一样了,以后有机会细讲)
4.关于小波变换的不足
这要看和谁比了。
A.作为图像处理方法,和多尺度几何分析方法(超小波)比:
对于图像这种二维信号的话,二维小波变换只能沿2个方向进行,对图像中点的信息表达还可以,但是对线就比较差。而图像中最重要的信息恰是那些边缘线,这时候ridgelet(脊波), curvelet(曲波)等多尺度几何分析方法就更有优势了。
B. 作为时频分析方法,和希尔伯特-黄变换(HHT)比:
相比于HHT等时频分析方法,小波依然没脱离海森堡测不准原理的束缚,某种尺度下,不能在时间和频率上同时具有很高的精度;以及小波是非适应性的,基函数选定了就不改了。
上面讲了那么多,仅仅也就是走进小波的大门,具体的我们还要学习子空间、多分辨率,母小波的变换,如何去构造想要的小波函数,然后还有离散小波变换,正交小波变换,二维小波变换,小波包的应用等。好像还有很多要学习的。
六、小波的应用
小波是多分辨率理论的分析基础。而多分辨率理论与多种分辨率下的信号表示和分析有关,其优势很明显--某种分辨率下无法发现的特性在另一个分辨率下将很容易被发现。从多分辨率的角度来审视小波变换,虽然解释小波变换的方式有很多,但这种方式能简化数学和物理的解释过程。
对于小波的应用很多,我学习的的方向主要是图像处理,所以这里用图像的应用来举例。对于图像,要知道量化级数决定了图像的分辨率,量化级数越高,图像越是清晰,图像的分辨率就高。
例一:哈尔小波图像分解

例二:小波去噪*滑

例三:小波的边缘检测

小波的知识还有很多,可以再继续看书学习,希望看到这个文章,可以对小波入门的同学有一定的帮助!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号