张量基础

最近在看汤晓欧 陈玉琨老师主编的《人工智能基础》(高中版) 这是一本入门好书，写得非常简单，适合我。

看到张量(tensor)这个概念的时候没太理解，在群里提问的时候，群里大神给予了耐心且详细的讲解，现整理一下。

零阶张量：普通的一个数，也就是我们说的标量(scalar)，就是零阶张量，对应到c语言，就是一个变量。

一阶张量：数学里的向量是一阶张量，也就是c语言里的一维数组。

二阶张量：数学里的矩阵，是二阶张量，也就是c语言中的二维数组。

三阶张量：就是对应到C语言中的三维数组。

例子1：
彩色图片有三个维度，长，宽，颜色，这三个东西构成了一个三阶张量。这里的颜色与RGB无关，只是单纯的表示颜色。

例子2：
再举个三阶张量的例子，下图三片矩阵组成在一起就是一个三阶张量。
具体形象化，就是如下形式：

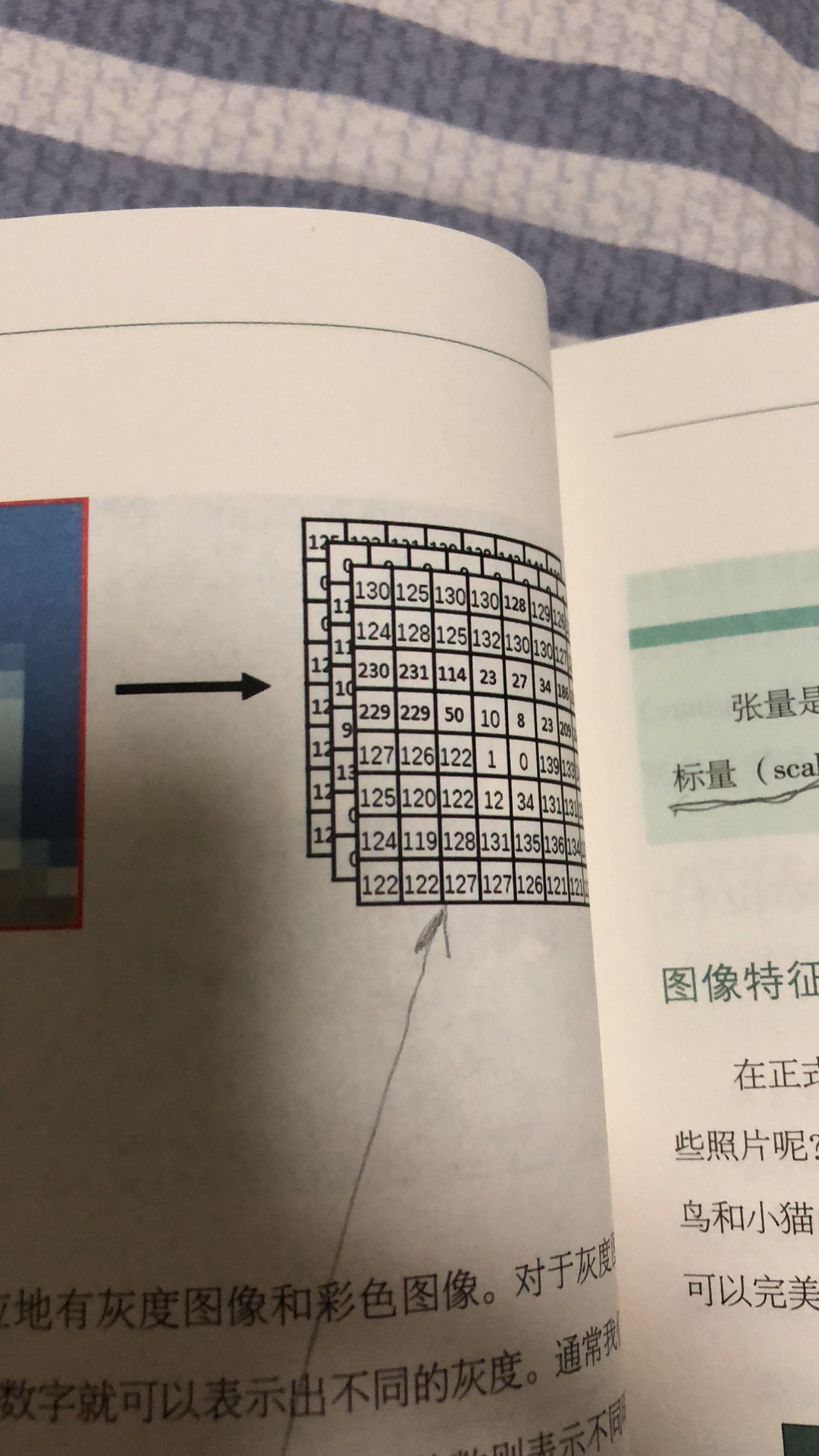
图中，矩阵的片数，也就是三阶张量的高度，也称为通道(channel)数。

图中是按照RGB三阶张量，每个通道的长和宽就是显示器的分辨率。

但是，三阶张量也不一定只有如上图所示的3片矩阵组成，也可能是4片矩阵或者5片矩阵，甚至更多片矩阵组成。也就是说，三阶张量的通道数
未必一定是3，也可能是4，5，... 甚至更多。只不过图中是表示彩色图像的三阶张量，只有RGB三个通道。矩阵可以看作是高度为1的三阶张量，即矩阵也就是通道为1的三阶张量。
因此，灰度(黑白)图像只有一个通道。

例子4：
用现实生活中的例子，长宽高构成了一个三维的物体，高就是第三个维度。一个长方体是由无数个二维的平面构成的。并不是只有三张平面构成。

四阶张量: C语言中的四维数组。
因为大家生活在三维表示的空间里，所以不太好具体形象描述三维以上的空间。但是电影《星际穿越》的结尾(我记得开头好像也有)有一段很形象的描述了四维空间是什么样。
有空要回去再看一看这部电影。就像有别的空间可能是真实存在的，比如也许天堂真的存在在第四个维度里，地狱在第i个维度里...（这里只是举了个例子）

...

N阶张量: 就是C语言中的N维数组。

最后，看我太笨了，大神的网友又举了一个很形象例子：

一张图片是三阶的，长，宽，颜色
一百张猫的图片是四阶的，长，宽，颜色，图片编号
不同物种的图片各100张是五阶的，长，宽，颜色，编号，物种

猫，1号图，长，宽，颜色
狗，20号图，长，宽，颜色
猪，1号图，长，宽，颜色

这里的猫，狗，猪就是物种。

张量运算：

卷积(convolution)：

进行两个向量的卷积时（图3-6），我们只需要沿着一个方向进行滑动；而进行两个矩阵的卷积时（图3-8），我们需要沿着横向和纵向两个方向进行滑动。

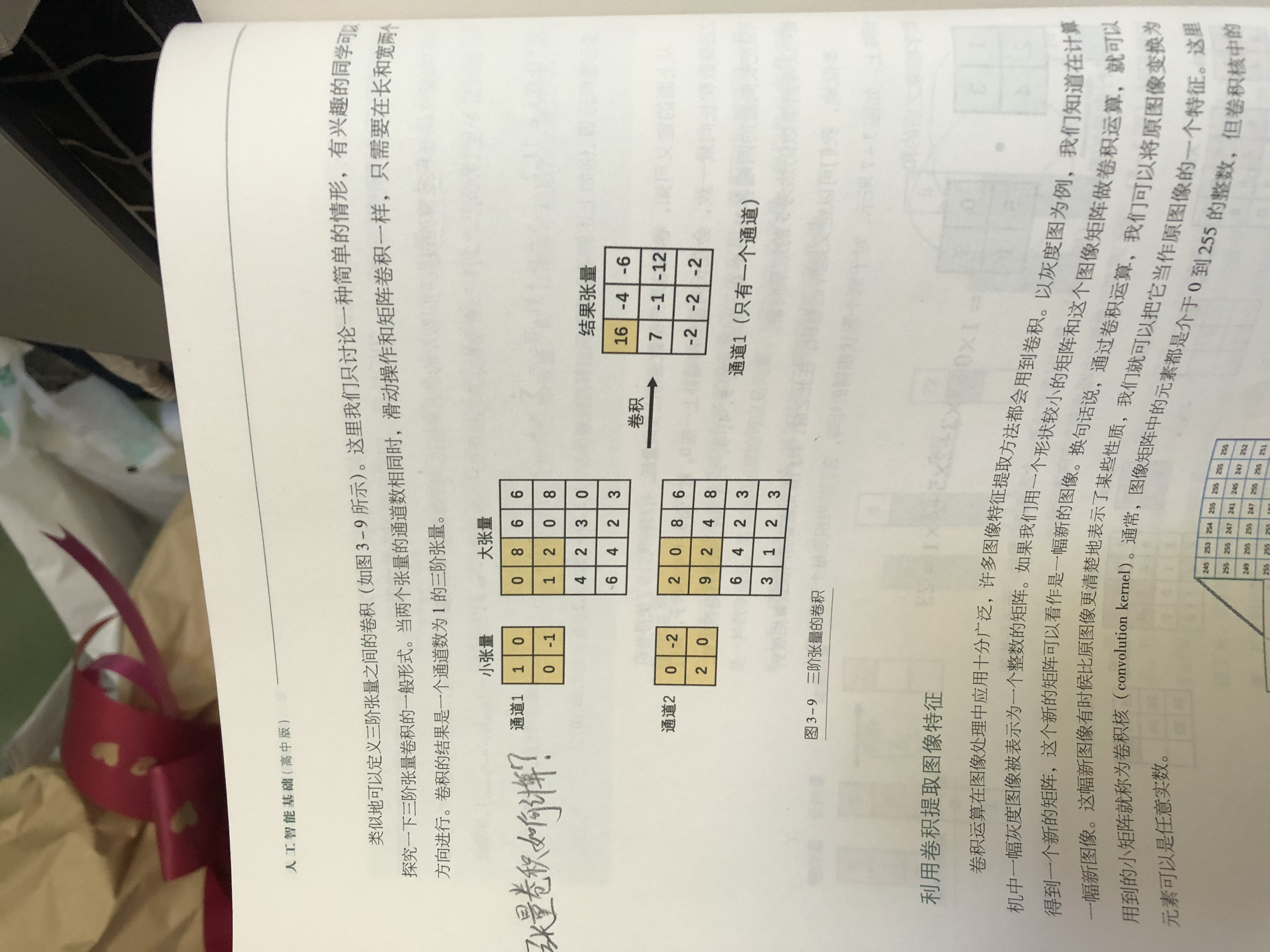
进行两个3阶张量做卷积时，这里假设3阶张量的通道大于1，也就是，3阶张量的高度不为1。则运算过程中，除了像两个矩阵那样，沿着横向和纵向移动，
还要沿着垂直于横纵两个方向进行移动。即，除了沿着矩阵的长和宽的方向移动，还要沿着高度进行移动。

参考：

《人工智能基础》（高中版） 汤晓鸥 陈玉琨 主编

某机器学习入门群 xx网友
http://www.maixj.net/misc/tensor-16661