sklearn标准化-【老鱼学sklearn】

在前面的一篇博文中关于计算房价中我们也大致提到了标准化的概念，也就是比如对于影响房价的参数中有面积和户型，面积的取值范围可以很广，它可以从0-500平米，而户型一般也就1-5。
标准化就是要把这两种参数的取值范围处于一个相对接近的地位，这样在进行梯度下降的计算中能够比较稳定地朝下落方向走，而不至于某个参数一调整步子迈得太大，而另一个参数一调整步子却又太小，有点像一个人的两条腿长短差距很大，走路就会不稳。

另外，Normalization在机器学习中也有叫归一化的，归一化相当于标准化的具体表现，因为取值范围都落到1中。这几个叫法都类似，基本可以认为是同一概念。

关于标准化，也可以参考吴恩达的视频（需FQ）：https://www.coursera.org/learn/machine-learning/lecture/xx3Da/gradient-descent-in-practice-i-feature-scaling

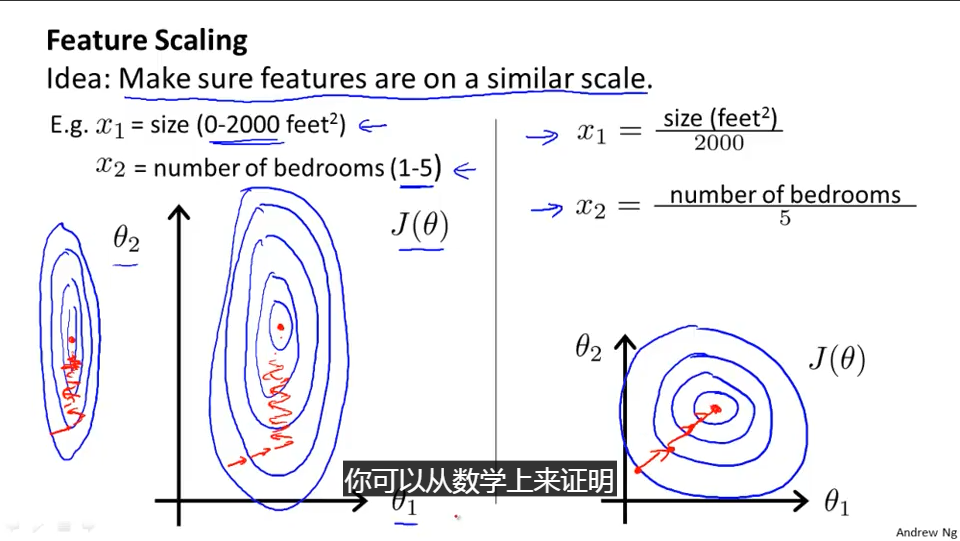
标准化的算法其实很简单，就是把值的结果映射成0到1之间，而映射规则就是除以这些值中最大范围就可以，前面讲的是基本思想，实际的计算公式推导，尤其是开始值不是从0开始如何映射，应该也不复杂，各位读者如果有兴趣自己推导下就可以。
不过sklearn提供了相关的scale方法，例子如下：

import numpy as np
from sklearn import preprocessing

a = np.array([[60, 2, 1],
              [150, 3, 3],
              [136, 3, 11]], dtype=np.float)
print("a=")
print(a)
print("scale(a)=")
print(preprocessing.minmax_scale(a))

输出为：

a=
[[  60.    2.    1.]
 [ 150.    3.    3.]
 [ 136.    3.   11.]]
scale(a)=
[[ 0.          0.          0.        ]
 [ 1.          1.          0.2       ]
 [ 0.84444444  1.          1.        ]]

在这个例子中定义了a变量，这个变量有三列，可以看成是有三个属性，例如我们假定第一列是房子的面积，其面积有：60、150、136平米，第二列是户型，分别是2房、3房和3房，第三列是楼层，分别位于1楼、3楼和11楼。
接着就通过正则化函数之后，它们变成了比较接近的数值。

在正则化函数中，也可以直接使用scale进行正则化，例如：

import numpy as np
from sklearn import preprocessing

a = np.array([[60, 2, 1],
              [150, 3, 3],
              [136, 3, 11]], dtype=np.float)
print("a=")
print(a)
print("scale(a)=")
print(preprocessing.scale(a))

输出为：

a=
[[  60.    2.    1.]
 [ 150.    3.    3.]
 [ 136.    3.   11.]]
scale(a)=
[[-1.39936232 -1.41421356 -0.9258201 ]
 [ 0.87670892  0.70710678 -0.46291005]
 [ 0.5226534   0.70710678  1.38873015]]

这个函数也能把各个属性的数据大小调整到比较一致的范围之内。

下面我们来看下正则化对机器学习性能的影响。
这里提一下机器学习的性能，在计算机系统中关于性能是指计算机的运行速度是否快速，而在机器学习中性能是指机器学习的效果如何，也就是类似预测的准确度是否高，得分是否高。

这里我们用一个例子来对比对数据进行正则化前后的预测得分高低情况：

首先创建用于分类的数据：

from sklearn.datasets.samples_generator import make_classification
# 生成300个数据，有2个特征，random_state设置了一个随机数的种子，这样每次运行都能得到相同的数据集
X, y = make_classification(n_samples=300, n_features=2, n_redundant=0, n_informative=2, random_state=89, n_clusters_per_class=1, scale=100)
print(X)

输出的数据为：

[[  68.29536774  -49.00310223]
 [ 122.44132212  -51.78441945]
 [  25.01641248 -111.93797795]
 [-110.32508254   52.9854327 ]
 [ 112.36845122  -77.57517306]
 [ 146.53631135 -107.44971166]
 [ 127.33837644 -117.57349528]
 [ 185.96222021  -90.25085534]
 [ 141.10711953 -112.51420661]

这里y值的输出类似为：

 0 1 0 1 1 0 1 0 0 1 1 1 0 1 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 0 1 1 1 1
 0 1 1 0]

也就是有两个分类，分别为0和1。

我们把X和y的数据在图形上观察一下，这里X有两列相关数据，同时用y值作为分类颜色进行显示，相关添加的代码片段为：

import matplotlib.pyplot as plt


plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()

显示出的图形为：

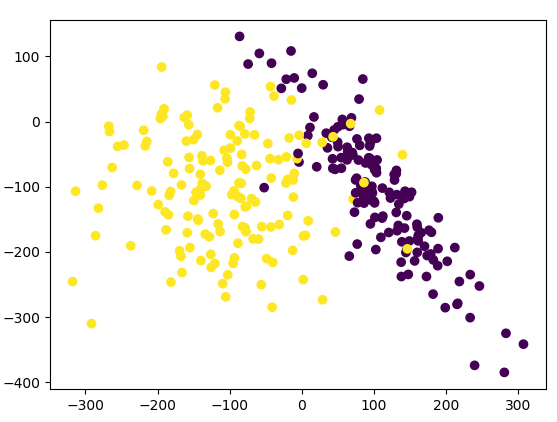
下面我们对其中的数据分割成训练集和测试集，并用SVC(Support Vector Classifier，支持向量机)算法进行训练并计算其得分，全部的代码为：

from sklearn.datasets.samples_generator import make_classification
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC

# 生成300个数据，有2个特征，random_state设置了一个随机数的种子，这样每次运行都能得到相同的数据集
X, y = make_classification(n_samples=300, n_features=2, n_redundant=0, n_informative=2, random_state=89, n_clusters_per_class=1, scale=100)

# 把数据集分割成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 创建SVC算法模型
model = SVC()
# 对训练数据进行训练
model.fit(X_train, y_train)
# 测试结果得分
print(model.score(X_test, y_test))

输出为：

0.455555555556

也就是在未进行正则化时模型的得分为45分。
下面我们来看下对原始数据进行正则化之后的模型得分情况：

from sklearn.datasets.samples_generator import make_classification
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn import preprocessing

# 生成300个数据，有2个特征，random_state设置了一个随机数的种子，这样每次运行都能得到相同的数据集
X, y = make_classification(n_samples=300, n_features=2, n_redundant=0, n_informative=2, random_state=89, n_clusters_per_class=1, scale=100)
# 正则化数据
X = preprocessing.scale(X)

# 把数据集分割成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
# 创建SVC算法模型
model = SVC()
# 对训练数据进行训练
model.fit(X_train, y_train)
# 测试结果得分
print(model.score(X_test, y_test))

输出为：

0.933333333333

这样得分就提高到了93分，相当于有93%的准确率。
因此，如果数据集中各个属性之间数值取值范围差异比较大的话，可以通过标准化来提高机器学习的性能。