sklearn模型的属性与功能-【老鱼学sklearn】

本节主要讲述模型中的各种属性及其含义。

例如上个博文中，我们有用线性回归模型来拟合房价。

# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(X_train, y_train)
# 打印出预测的前5条房价数据
print("预测的前5条房价数据:")
print(model.predict(X_test)[:5])

在sklearn中使用各种模型时都用了一种统一的样式，基本上都是先用fit()进行训练，然后用predict()进行预测。

对于线性回归模型，其数学模型基本上类似：

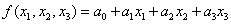
这里我们只提供了三个属性(x1, x2, x3)作为示例进行描述，在训练时本质上就是不停地调整a0, a1, a2, a3的参数，使其最终预测的f值与实际的y值之间的差值最小化，这里的差值一般用差的平方和来表示。

对于我们前面的房价例子中，当模型进行了fit()之后，相当于构建了上述的线性方程，那这个方程中的系数是多少呢？也就是上面的a1,a2,a3等这些系数值是多少呢？我们有没有办法把它打印出来呢？

我们可以通过：

print(model.coef_)

打印出这个线性方程前的系数：

[ -6.87376243e-02   3.32843076e-02   4.06433614e-02   1.75803112e+00
  -1.87184969e+01   3.85410965e+00   2.32212165e-02  -1.23775798e+00
   3.03653042e-01  -1.08755181e-02  -1.01367357e+00   9.56725087e-03
  -6.08759683e-01]

这里总共有13个系数值，为何有13个系数值呢？
因为我们在预测房价时认为影响房价总共有13个参数，并且我们在训练的数据集中就获得了这13个属性值，这样相应地就有13个自变量，13个自变量的系数值。

但我们知道，在线性方程中还有一个常量值，也称为截距，相当于某个房价的平均值或基准值的概念（当然这里的命名有点不那么标准，希望读者能够自己去体会），也就是此值代表的是当各个属性值都为0时所代表的房价值。
如何打印出这个常量值呢？

print(model.intercept_)

输出为：

35.6839415854

相当于当某房子的房龄为0，户型为0房时等这些条件下，房价为35万这样的理解方式。

这里sklearn用coef_和intercept_对系数和截距进行了命名，这两个名字的全称为：coefficient（系数）和intercept（截距）

其实通过系数值，我们还能获得如下信息：
. 此系数中如果是+号，表示是正相关，如果是-号表示是负相关；
. 如果系数值越大，则说明其对最终房价的影响度就越大，当然，这是在其变量值是同等度量的情况下。

经过上面参数预测出来的结果跟实际值之间到底差距多少呢？
这里可以通过score来进行表述，这个得分的实现方式在sklearn中分简单，例子如下：

print("得分：", model.score(X_test, y_test))

输出为：

得分： 0.630433028896

这里得分为0-1的值，可以简单认为是63分，看来当前房价的预测准确度不是很高，只有63分。
这里的打分计算公式类似均方差的概念，也就是预测值与实际值之差的平方和再开方，然后除以实际值与实际平均值之差的平方再开方之类的，具体计算公式是什么样的，可以在IDEA中查看相应score函数的说明文档就可以。