Digital Filter Design

Digital Filter Design

 

 

Introduction

The purpose of this book is to provide you with different theorethical and practical approaches to digital filter design. The book covers design of both finite and infinite impulse response filters. In addition, it applies the most popular and most commonly used design methodes giving the best solutions. Intuitive explanations and numerous examples contained herein will help you to devolope your understanding of these methods and test your knowledge on concrete issues.

 

---

1.1 Basic concepts of digital filtering

Digital filtering has specific characteristics that you need to pay special attention to. The analog input signal must satisfy certain requirements. Furthermore, on converting an output digital signal into analog form, it is necessary to perform additional signal processing in order to obtain the appropriate result.

Figure 1-1 shows the block diagram of digital filtering process.

Figure 1-1. Digital filtering

The process of converting an analog signal into digital form is performed by sampling with a finite sampling frequency fs. If an input signal contains frequency components higher than half the sampling frequency (fs/2), it will cause distortion to the original spectrum. This is the reason why it is first necessary to perform filtering of an input signal using a low-pass filter that eliminates high-frequency components from input frequency spectrum. This filter is called anti-aliasing filter as it prevents aliasing.

After the process of filtering and sampling, a digital signal is ready for further processing which, in this case, is filtering using the appropriate digital filter. The output signal is also a digital signal which, in some cases, needs to be converted back into analog form. After digital-to-analog conversion, signal contains some frequency components higher than fs/2 that must be eliminated. Again, it is necessary to use a low-pass filter with the sampling frequency fs/2. The specific characteristics of conversion affecting the signal are beyond the scope of this book.

Digital filter attenuation is usually expressed in terms of the logarithmic decibel scale (dB). The attenuation measured in decibels can be found using the following expression:

a = 20 * log(H(f))

Cut-off frequencies are used for filter specification, which will be discussed later. The cut-off frequency of the passband is a frequency at which the transition of the passband to the transition region occurs. The cut-off frequency of the stopband is a frequency at which the transition of the transition region to the stopband occurs. These two frequencies are equivalent only for the ideal filter which is not possible to realize in practice. In other words, they are always different.

 

1.2.Types of digital filters

Filters can be classified in several different groups, depending on what criteria are used for classification. The two major types of digital filters are finite impulse response digital filters (FIR filters) and infinite impulse response digital filters (IIR).

Both types have some advantages and disadvantages that should be carefully considered when designing a filter. Besides, it is necessary to take into account all fundamental characteristics of a signal to be filtered as these are very important when deciding which filter to use. In most cases, it is only one characteristic that really matters and it is whether it is necessary that filter has linear phase characteristic or not.

Speech signal, for example, can be processed in the systems with non-linear phase characteristic. The phase characteristic of a speech signal is not of the essence and as such can be neglected, which results in the possibility to use much wider range of systems for its prosessing.

There are also signals for which the phase characteristic is of the essence. A typical example are signals obtained from various sensors in industry. Therefore, it is necessary that a filter has linear phase characteristic to prevent loosing important information.

When a signal to be filtered is analysed in this way, it is easy to decide which type of digital filter is best to use. Accordingly, if the phase characteristic is of the essence, FIR filters should be used as they have linear phase characteristic. Such filters are of higher order and more complex, therefore. Otherwise, when it is only frequency response that matters, it is preferable to use IIR digital filters which have far lower order, i.e. are less complex, and thus much easier to realize.

The basic characteristics of Finite Impulse Response (FIR) filters are:
 

• linear phase characteristic;

 

• high filter order (more complex circuits); and

 

• stability.

The basic characteristics of Infinite Impulse Response (IIR) are:
 

• non-linear phase characteristic;

 

• low filter order (less complex circuits); and

 

• resulting digital filter has the potential to become unstable.

---

 

2.1 Introduction

FIR filters are digital filters with finite impulse response. They are also known as non-recursive digital filters as they do not have the feedback (a recursive part of a filter), even though recursive algorithms can be used for FIR filter realization.

 

Figure 2-1-1. Block diagrams of FIR and IIR filters

 

FIR filters can be designed using different methods, but most of them are based on ideal filter approximation. The objective is not to achieve ideal characteristics, as it is impossible anyway, but to achieve sufficiently good characteristics of a filter. The transfer function of FIR filter approaches the ideal as the filter order increases, thus increasing the complexity and amount of time needed for processing input samples of a signal being filtered.

Figure 2-1-2. Ideal low-pass filter approximation

The resulting frequency response can be a monotone function or an oscillatory function within a certain frequency range. The waveform of frequency response depends on the method used in design process as well as on its parameters.

This book describes the most popular method for FIR filter design that uses window functions. The characteristics of the transfer function as well as its deviation from the ideal frequency response depend on the filter order and window function in use.

Each filter category has both advantages and disadvantages. This is the reason why it is so important to carefully choose category and type of a filter during design process.

FIR filters can have linear phase characteristic, which is not like IIR filters that will be discussed in Chapter 3. Obviously, in such cases when it is necessary to have a linear phase characteristic, FIR filters are the only option available. If the linear phase characteristic is not necessary, as is the case with processing speech signals, FIR filters are not good solution at all.

Figure 2-1-3 illustrates input and output signals of non-linear phase systems.

 

Figure 2-1-3. The effect of non-linear phase characteristic

The system introduces a phase shift of 0 radians at the frequency of ω, and π radians at three times that frequency. Input signal consists of natural frequency ω and one harmonic with the same amplitude at three times that frequency. Figure 2-1-3. shows the block diagram of input signal (left) and output signal (right). It is obvious that these two signals have different waveforms. The power of signals is not changed, nor the amplitudes of harmonics, only the phase of the second harmonic is changed.

If we assume that the input is a speech signal whose phase characteristic is not of the essence, such distortion in the phase of the signal would be unimportant. In this case, the system satisfies all necessary requirements. However, if the phase characteristic is of importance, such a great distortion mustn’t be allowed.

In order that the phase characteristic of a FIR filter is linear, the impulse response must be symmetric or anti-symmetric, which is expressed in the following way:

h[n] = h[N-n-1] ; symmetric impulse response (about its middle element)

h[n] = -h[N-n-1] ; anti-symmetric impulse response (about its middle element)

One of the drawbacks of FIR filters is a high order of designed filter. The order of FIR filter is remarkably higher compared to an IIR filter with the same frequency response. This is the reason why it is so important to use FIR filters only when the linear phase characteristic is very important.

A number of delay lines contained in a filter, i.e. a number of input samples that should be saved for the purpose of computing the output sample, determines the order of a filter. For example, if the filter is assumed to be of order 10, it means that it is necessary to save 10 input samples preceeding the current sample. All eleven samples will affect the output sample of FIR filter.

The transform function of a typical FIR filter can be expressed as a polynomial of a complex variable z-¹. All the poles of the transfer function are located at the origin. For this reason, FIR filters are guaranteed to be stable, whereas IIR filters have potential to become unstable.

 

2.2 Finite impulse response (FIR) filter design methods

Book: Digital Filter Design

Table of 
Contents

 

 

Most FIR filter design methods are based on ideal filter approximation. The resulting filter approximates the ideal characteristic as the filter order increases, thus making the filter and its implementation more complex.

The filter design process starts with specifications and requirements of the desirable FIR filter. Which method is to be used in the filter design process depends on the filter specifications and implementation. This chapter discusses the FIR filter design method using window functions.

Each of the given methods has its advantages and disadvantages. Thus, it is very important to carefully choose the right method for FIR filter design. Due to its simplicity and efficiency, the window method is most commonly used method for designing filters. The sampling frequency method is easy to use, but filters designed this way have small attenuation in the stopband.

As we have mentioned above, the design process starts with the specification of desirable FIR filter.

2.2.1 Basic concepts and FIR filter specification

First of all, it is necessay to learn the basic concepts that will be used further in this book. You should be aware that without being familiar with these concepts, it is not possible to understand analyses and synthesis of digital filters.

Figure 2-2-1 illustrates a low-pass digital filter specification. The word specification actually refers to the frequency response specification.

 

Figure 2-2-1a. Low-pass digital filter specification

 

 

 

 

Figure2-2-1b. Low-pass digital filter specification

 

• • ωp – normalized cut-off frequency in the passband;

 

• • ωs – normalized cut-off frequency in the stopband;

 

• • δ1 – maximum ripples in the passband;

 

• • δ2 – minimum attenuation in the stopband [dB];

 

• • ap – maximum ripples in the passband; and

 

• • as – minimum attenuation in the stopband [dB].

 

Frequency normalization can be expressed as follows:

where:
 

• • fs is a sampling frequency;

 

• • f is a frequency to normalize; and

 

• • ω is normalized frequency.

Specifications for high-pass, band-pass and band-stop filters are defined almost the same way as those for low-pass filters. Figure 2-2-2 illustrates a high-pass filter specification.

 

Figure 2-2-2a. High-pass digital filter specification

 

 

 

 

Figure 2-2-2b. High-pass digital filter specification

Comparing these two figures 2-2-1 and 2-2-2, it is obvious that low-pass and high-pass filters have similar specifications. The same values are defined in both cases with the difference that in the later case the passband is substituded by the stopband and vice versa.

Figure 2-2-3 illustrates a band-pass filter specification.

 

Figure 2-2-3a. Band-pass digital filter specification

 

 

 

 

Figure 2-2-3b. Band-pass digital filter specification

Figure 2-2-4 illustrates a band-stop digital filter specification.

 

Figure 2-2-4a. Band-stop digital filter specification

 

 

 

 

Figure 2-2-4b. Band-stop digital filter specification

 

2.2.2 Z-transform

The Z-transform is performed upon discrete-time signals. It converts a discrete time-domain signal into a complex frequency-domain representation. It is very suitable for analysing discrete time-domain signals and systems. The z-transform is derived from the Fourier discrete time-domain transformation and is considered the basic operation in digital filter design process.

The Z-transform is defined as:

where z is the complex number.

Example:

Assume that samples of a discrete-time signal x(n) are known. It is necessary to transform this signal through the ztransform and Fourier fransform.

x(n)={1,2,3,4,5,4,3,2,1} ; 0 ≤ n ≤ 8

z-transform is defined as follows:

It becomes:

The last expression represents the z-transform of the given signal.

The Fourier transform can be found by rewriting the previous expression in terms of z as z=ejω. It further becomes:

Figure 2-2-5 illustrates the frequency spectrum of the given signal.

 

Figure 2-2-5. Frequency spectrum of the given signal

Comparing Z and Fourier transforms, it is easy to notice some similarities between them:

In polar coordinate system, the complex number z may be expressed as:

The two last expressions lead us to the conclusion that the Fourier transform is just a special form of the z-transform for r=1.
In the z plane, the Fourier transform is represented as a unit circle, which can be seen in Figure 2-2-6 below.

 

Figure 2-2-6. Fourier transform in the z plane

 

2.2.2.1 Transform function of discrete-time systems

The Z-transform is primarily used for finding the transfer function of linear discrete-time systems. When the transfer function is found, it is necessary to consider its zeros and poles in the z plane. The transfer function of discrete-time systems is defined as:

where:
 

• • bi are the feedforward filter coefficients (non-recursive part);

 

• • aj are the feedback filter coefficients (recursive part);

 

• • H0 is a constant;

 

• • qi are the zeros of the transfer function; and

 

• • pj are the poles of the transfer function.

The recursive part of the transfer function is actually a feedback of discrete-time system. As we previously mentioned, FIR filters do not have this recursive part of the transfer function, so the expression above can be simplified in the following way:

The impulse response of discrete-time system is obtained from inverse z-transform of the transfer function i.e. the transfer function of discrete-time system is actually the Z-transform of impulse response:

where h(n) is the impulse response of discrete-time system.

 

Figure 2-2-7. Block diagram of a linear discrete-time system

In the time domain, the discrete-time system, shown in Figure 2-2-7, can also be expressed as the convolution of the input signal x(n) and the impulse response h(n) of the system:

In the frequency domain, the discrete-time system, shown in Figure 2-2-7, can be expressed as the multiplication of the Z-transform input signal X(z) and the transfer function H(z) of the system:

which further gives:

The first way of representing discrete-time systems is more suitable for software implementation itself, whereas the later is more suitable for analyse, hardware implementation (described later) and synthesis, i.e. discrete-time system design.

Example:

The impulse response of a 10-th order FIR filter designed using the Hamming window (discussed in the next chapter) is:

h(n) = {0, - 0.0127, - 0.0248, 0.0638, 0.2761, 0.4, 0.2761, 0.0638, - 0.0248, - 0.0127, 0}

The transfer function of this filter is found via the ztransform of impulse response:

Using the following expression:

it is possible to yield the transfer function of the fixed normalized frequency. If for example ω = 0.2π then:

One example of hardware realization of this filter is illustrated in Figure 2-2-8.

 

Figure 2-2-8. FIR filter realization

Software realization requires a buffer of minimum length 9. Buffers are usually circular and their length can be expressed as 2^n, which in this case means that the circular buffer is of length 16=2^4.

2.2.2.2 Effect of the poles and zeros of the transfer function

The location of zeros and poles of the transfer function is very important for discretetime system analyses and synthesis. According to their position it is possible to test stability of a discrete-time system, detect round-off errors made due to software implementation of a filter as well as errors in the coefficients encountered during hardware implementation of a filter.

In order that a discrete-time system is stable, all poles of the discrete-time system transfer function must be located inside the unit circle, as shown in Figure 2-2-6. If this requirement is not satisfied, the system becomes unstable, which is very dangerous. The location of zeros doesn’t affect the stabilty of discrete-time systems. Recalling that FIR flters do not have a feedback, which further means that the transfer function has no poles. This causes a FIR filter to be always stable. Filter stability will be discussed in more details along with IIR filters which have potential to become unstable because of the feedback they have. This property of FIR filters actually represents their essential adventage. From now on, only the zeros of the transfer function will be discussed in this chapter.

An error in coefficient representation is always produced due to software and hardware implementation. In software implementation, an error is triggered by the finite word-length effect, whereas in hardware implementation, it ocurrs due to impossibility of representing the coefficients with absolute accuracy. The result in both cases is that the value of coefficients differs from their value obtained in design process. Such errors cause frequency deviation of discrete-time system designed.

Frequency deviation depends on the spacing between the zeros of the FIR filter transfer function. FIR filter coefficient error affects more the frequency characteristic as the spacing between the zeros of the transfer function narrows. This property is particularly typical of highorder filters because their zeros are very close each other. However, slight errors in coefficient representation may cause large frequency deviations.

Figure 2-2-9 illustrates the required and obtained frequency characteristic of a FIR filter. The finite word-length effect on the transform function of a FIR filter is clearly marked. Assume that a 50-th order low-pass FIR filter with normalized cut-off frequency of 0.25 Hz is designed using the Hann window.

 

Figure 2-2-9. Deviation from required frequency characteristic

The frequency deviation shown in Figure 2-2-9 is basically slight deviation, even though it is very large at certain points. The minimum attenuation and the width of transition region of the resulting IIR filter remain unchanged, so that such deviation is acceptable. However, as this is not a common case, it is necessary to be very careful when designing high order filters because the transfer function zeros get closer, while more affecting the resulting frequency characteristic.

2.2.3 Ideal filter approximation

The ideal filter frequency response is used when designing FIR filters using window functions. The objective is to compute the ideal filter samples. FIR filters have finite impulse response, which means the ideal filter frequency sampling must be performed in a finite number of points. As the ideal filter frequency response is infinite, it is easy to produce sampling errors. The error is less as the filter order increases.

Figure 2-2-10 illustrates the transfer functions of four standard ideal filters.

 

Figure 2-2-10. Transfer functions of four standard ideal filters

The ideal filter frequency response can be computed via inverse Fourier transform. The four standard ideal filters frequency responses are contained in the table 2-2-1 below.

 

Table 2-2-1. The frequency responses of four standard ideal filters

The value of variable n ranges between 0 and N, where N is the filter order. A constant M can be expressed as M = N / 2. Equivalently, N can be expressed as N = 2M.

The constant M is an integer if the filter order N is even, which is not the case with odd order filters. If M is an integer (even filter order), the ideal filter frequency response is symmetric about its Mth sample which is found via expression shown in the table 2-2-1 above. If M is not an integer, the ideal filter frequency response is still symmetric, but not about some frequency response sample.

Since the variable n ranges between 0 and N, the ideal filter frequency response has N+1 sample.

If it is needed to find frequency response of a non-standard ideal filter, the expression for inverse Fourier transform must be used:

Non-standard filters are rarely used. However, if there is a need to use some of them, the integral above must be computed via various numerical methodes.

2.2.4 FIR filter design using window functions

The FIR filter design process via window functions can be split into several steps:
 

1. 1. Defining filter specifications;

 

1. 1. Specifying a window function according to the filter specifications;

 

1. 1. Computing the filter order required for a given set of specifications;

 

1. 1. Computing the window function coefficients;

 

1. 1. Computing the ideal filter coefficients according to the filter order;

 

1. 1. Computing FIR filter coefficients according to the obtained window function and ideal filter coefficients;

 

1. 1. If the resulting filter has too wide or too narrow transition region, it is necessary to change the filter order by increasing or decreasing it according to needs, and after that steps 4, 5 and 6 are iterated as many times as needed.

The final objective of defining filter specifications is to find the desired normalized frequencies (ωc, ωc1, ωc2), transition width and stopband attenuation. The window function and filter order are both specified according to these parameters.

Accordingly, the selected window function must satisfy the given specifications. This point will be discussed im more detail in the next chapter (2.3).

After this step, that is, when the window function is known, we can compute the filter order required for a given set of specifications. One of the techniques for computing is provided in chapter 2.3.

When both the window function and filter order are known, it is possible to calculate the window function coefficients w[n] using the formula for the specified window function. This issue is also covered in the next chapter.

After estimating the window function coefficients, it is necessary to find the ideal filter frequency samples. The expressions used for computing these samples are discussed in section 2.2.3 under Ideal filter approximation. The final objective of this step is to obtain the coefficients hd[n]. Two sequencies w[n] and hd[n] have the same number of elements.

The next step is to compute the frequency response of designed filter h[n] using the following expression:

Lastly, the transfer function of designed filter will be found by transforming impulse response via Fourier transform:

or via Z-transform:

If the transition region of designed filter is wider than needed, it is necessary to increase the filter order, reestimate the window function coefficients and ideal filter frequency samples, multiply them in order to obtain the frequency response of designed filter and reestimate the transfer function as well. If the transition region is narrower than needed, the filter order can be decreased for the purpose of optimizing hardware and/or software resources. It is also necessary to reestimate the filter frequency coefficients after that. For the sake of precise estimates, the filter order should be decreased or increased by 1.

2.2.5 FIR filter realization

FIR filter transfer function can be expressed as:

The frequency response realized in the time domain is of more interest for FIR filter realization (both hardware and software). The transfer function can be found via the z-transform of a FIR filter frequency response. FIR filter output samples can be computed using the following expression:

where:
 

• • x[k] are FIR filter input samples;

 

• • h[k] are the coefficients of FIR filter frequency response; and

 

• • y[n] are FIR filter output samples.

A good property of FIR filters is that they are less sensitive to the accuracy of constants than IIR filters of the same order.

There are several types of FIR filter realization. This chapter covers direct, direct transpose and cascade realizations which are very convenient for the hardware implementation of a filter. As for the software implementation, direct and optimized realizations will be discussed in this book.

2.2.5.1 Direct realization

Direct realization of FIR filter is based on the direct implementation of this expression:

Direct realization is also known as a transversal filter.

Figure 2-2-11 illustrates the block diagram describing the hardware direct realization of a FIR filter.

 

Figure 2-2-11. FIR filter direct realization

For direct realization structure, the multiplication constants are the same as the transfer function coefficients, i.e. the FIR filter frequency response coefficients.

As for software direct realization of the FIR filter, it is necessary to provide a buffer for minimum N samples, where N is the number of FIR filter coefficients. For its simplicity and speed, most commonly used buffer is so called circular buffer the length of which can be expressed as 2^k. The value of the constant k is a minimum value for which the expression N ≤ 2^k is valid. Accordingly:

where the operatorrepresents rounding down to a less value.

 

Figure 2-2-12. Circular buffer of length 16 = 2^4

The algorithm used for software direct realization of FIR filter consists of:
 

1. 1. Reading the samples of a signal being filtered;

 

1. 1. Storing a new sample on the first available location; and

 

1. 1. Performing a convolution operation upon filter coefficients (frequency response coefficients), resulting in a FIR filter output sample.

Since the buffer is 16 bits wide, circular buffer addressing is performed using addressing mode 16:

Example: Assuming that a filter used in this example is a 5th order FIR filter. Design this filter using direct realization with circular buffer. The buffer length needs to be 2^k.

The buffer length is obtained in the following way:

This means that the minimum length of circular buffer is 2^3 = 8.

The contents of the buffer after receiving the first 10 samples is shown in the table 2-2-2. Input samples are denoted by x[n], whereas the shaded cells denote buffer locations that have been changed. 

STEP	ADDR. 7	ADDR. 6	ADDR. 5	ADDR. 4	ADDR. 3	ADDR. 2	ADDR. 1	ADDR. 0
0
1								x[0]
2							x[1]	x[0]
3						x[2]	x[1]	x[0]
4					x[3]	x[2]	x[1]	x[0]
5				x[4]	x[3]	x[2]	x[1]	x[0]
6			x[5]	x[4]	x[3]	x[2]	x[1]	x[0]
7		x[6]	x[5]	x[4]	x[3]	x[2]	x[1]	x[0]
8	x[7]	x[6]	x[5]	x[4]	x[3]	x[2]	x[1]	x[0]
9	x[7]	x[6]	x[5]	x[4]	x[3]	x[2]	x[1]	x[8]
10	x[7]	x[6]	x[5]	x[4]	x[3]	x[2]	x[9]	x[8]

Table 2-2-2. Input circular buffer after receiving 10 samples

For software realization, filtering of input samples is performed as per formula below:

 

2.2.5.2 Direct transpose realization

Direct transpose realization is similar to direct realization in many ways. Speaking about software implementation, the direct transpose realization must also have a buffer of minimum length N, where N is the number of FIR filter coefficients.

Figure 2-2-13 illustrates the block diagram describing hardware direct transpose realization of a FIR filter.

 

Figure 2-2-13. Direct transpose realization of a FIR filter

There are no significant differences between direct and direct transpose realizations. Both structures have the same number of delay elements, the same number of multipliers and the same coefficients to perform multiplication upon.

2.2.5.3 Cascade realization

Cascade realization, very convenient for its modular structure, is commonly used for FIR filter hardware realization. When using this realization, a filter is divided into several low-order sections. The second-order sections are most commonly used. Individual sections are mostly in direct form realization, although they can also be in direct transpose form realization. The cascade realization is normally used for higher order filter realization.

The transfer function of the cascade realization looks as follows:

where:
 

• • M is the number of sections; and

 

• • ak1, ak2 are the multiplication coefficients of section k.

Figure 2-2-14 illustrates the block diagram describing the hardware cascade realization of a FIR filter.

 

Figure 2-2-14. FIR filter cascade realization

The number of multipliers, adders and delays is the same as for direct realization. The main advantage of the cascade realization is its modularity, otherwise very convenient for hardware implementation. The cascade of second order sections is important for the realization of the filters of arbitrary order.

2.2.5.4 Optimized realization

Optimized realization has less, but more demanding multipliers for realization. This realization is most commonly used for software implementation of FIR filters, because a reduction in the number of multipliers enhances the process of convolution (samples filtering process).

Optimized realization utilizes the symmetry of frequency response coefficients. There are also anti-symmetric FIR filters that are beyond the scope of this book. Anyway, the optimized realization may be used for these filters as well.

The symmetry of the coefficients of FIR filter frequency response can be expressed by equation below:

This symmetry makes it possible for the transfer function to be expressed as follows:

Figure 2-2-15 illustrates the block diagram of optimized realization for even N, whereas Figure 2-2-16 illustrates that for odd N.

 

Figure 2-2-15. Optimized realization for odd frequency response

 

 

 

 

Figure 2-2-16. Optimized realization for even frequency response

2.3 Window functions

The window method is most commonly used method for designing FIR filters. The simplicity of design process makes this method very popular.

A window is a finite array consisting of coefficients selected to satisfy the desirable requirements. This chapter provides a few methods for estimating coefficients and basic characteristics of the window itself as well as the result filters designed using these coefficients. The point is to find these coefficients denoted by w[n].

When designing digital FIR filters using window functions it is necessary to specify:
 

• • A window function to be used; and

 

• • The filter order according to the required specifications (selectivity and stopband attenuation).

These two requirements are interrelated. Each function is a kind of compromise between the two following requirements:
 

• • The higher the selectivity, i.e. the narrower the transition region; and

 

• • The higher suppression of undesirable spectrum, i.e. the higher the stopband attenuation.

Table 2-3-1 below contains all window functions mentioned in this chapter and briefly compares their selectivity and stopband attenuation. 

WINDOW FUNCTION	NORMALIZED LENGTH OF THE MAIN LOBE FOR N=20	TRANSITION REGION FOR N=20	MINIMUM STOPBAND ATTENUATION OF WINDOW FUNCTION	MINIMUM STOPBAND ATTENUATION OF DESIGNED FILTER
Rectangular	0.1π	0.041π	13 dB	21 dB
Triangular (Bartlett)	0.2π	0.11π	26 dB	26 dB
Hann	0.21π	0.12π	31 dB	44 dB
Bartlett-Hanning	0.21π	0.13π	36 dB	39 dB
Hamming	0.23π	0.14π	41 dB	53 dB
Bohman	0.31π	0.2π	46 dB	51 dB
Blackman	0.32π	0.2π	58 dB	75 dB
Blackman-Harris	0.43π	0.32π	91 dB	109 dB

  

Table 2-3-1. Comparison of window functions

Special attention should be paid to the fact that minimum attenuation of window function and that of the filter designed using that function are different in most cases. The difference, i.e. additional attenuation occurs under the process of designing a filter using window functions. This affects the stopband attenuation to become additionally higher, which is very desirable.

However, a drawback of this method is that the minimum stopband attenuation is fixed for each function. The exception is the Kaiser window described later in this chapter.

The following concepts such as the main lobe, main lobe width, side lobes, transition region, minimum stopband attenuation of window function and minimum stopband attenuation of designed filter are described in more detail in Figure 2-3-1.

 

Figure 2-3-1. Main lobe, main lobe width, side lobes, transition region

As can be seen in the table 2-3-1 above, the stopband attenuation of these windows is not adjustable. It is only possible to affect the transition region by increasing the filter order. For this reason it is preferable to start design process by specifying the appropriate window function on the basis of the stopband attenuation. It is most preferable to specify a window with the least stopband attenuation that satisfies the given requirements. This enables the designed filter to have the narrowest transition region.

Example:

Design a filter with the following characteristics:
 

1. 1. Minimum stopband attenuation is 40dB;

 

1. 1. Transition region between 2KHz and 3KHz; and

 

1. 1. Sampling frequency 10KHz.

Looking at the table 2-3-1 above (last column), it is obvious that required attenuation can be reached using the Hann window. Besides, such attenuation can be obtained using any other window following the Hann window (all the functions are sorted according to their stopband attenuation), thus the higher stopband attenuation would be at a cost of the wider transition region for the same filter order. Since the filter specification also includes transition region, this would further result in increasing the filter order and its complexity as well.

After specifying the suitable window function, it is necessary to compute the filter order. The cut-off frequencies of transition regions are normalized first.
 

• • The sampling frequency is fs=10KHz;

 

• • The lower cut-off frequency of transition region is f1=2KHz; and

 

• • The upper cut-off frequency of transition region is f2=3KHz.

Normalized frequencies are obtained in the following way:

Transition region of the Hann window is 0.12π for a 20th order filter. To satisfy the given specifications, the required transition region is expressed as:

fn2 - fn1 = 0.2π

Since the required transition region is wider than that of a 20th order filter, the filter order needs to be less than 20. It is found via iteration. Roughly estimated, the initial solution in this case can be a 12th order filter. The required order is somewhat higher and is found after performing several iterations. The resulting filter order is 16.

Filter Designer Tool is used for obtaining a first-order filter. The table 2-3-2 provides performed iterations and other important information. 

NUMBER OF ITERATION	FILTER ORDER	FILTER ATTENUATION AT 3KHZ
1	12	25 dB
2	14	33 dB
3	16	49 dB
4	15	38 dB

Table 2-3-2. Calculating filter order

After specifying the window function and filter order, it is necessary to compute window coefficients w[n] using expressions for the specified window.

2.3.1 Rectangular Window

The rectangular window is rarely used for its low stopband attenuation. The first lobe (refer to Figure 2-3-2) has attenuation of 13dB and the narrowest transition region, therefore. A filter designed using this window has minimum stopband attenuation of 21 dB.

Unlike other window functions being a kind of compromise between requirements for as narrow transition region as possible and as high stopband attenuation as possible, this window is characterized by extreme values. Namely, the minimum transition region is achieved, but at a cost of stopband attenuation.

It is easy to find rectangular window coefficients as all coefficients between 0 and N-1 (N-filter order) are equal to 1, which can be expressed in the following way:

w[n] = 1; 0 ≤ n ≤ N−1

Note that the rectangular window performs selection of N samples from a sequence of input samples, but it does not perform sample scaling.

Figure 2-3-2 illustrates coefficients in the time-domain.

 

Figure 2-3-2. Rectangular window in the time domain

Figure 2-3-3 illustrates the frequency domain of rectangular window

 

Figure 2-3-3. Rectangular window in the frequency domain (spectrum)

For its less stopband attenuation, the rectangular window is not preferable for digital filter design. Such a less attenuation is a result of cut-off samples within a window (a sequence of sampled frequencies). Up to a zero sample (from which sampling starts), all sampled frequencies are equal to zero. The first sample represents a sudden jump to some value (non-zero sample). Exactly these sudden jumps result in producing relatively sharp high-frequency components which lessen the stopband attenuation.

The attenuation gets higher by making cut-off samples less sharp, which results in reducing filter selectivity, i.e. wider transition region. Since initial requirements of a digital filter are predefined and due to less selectivity, it is necessary to increase the filter order to narrow the transition region. Note the fact that the transition region is inversely proportional to the filter order N. The transition region narrows as the filter order increases.

Increase in filter order affects the filter to become more complex and need more time for sample processing. This is why it is very important to be careful when specifying the window function and filter order as well.

2.3.2 Triangular (Bartlett) window

The triangular (Bartlett) window is one among many functions that lessens the effects of final samples. Due to it, the stopband attenuation of this window is higher than that of the rectangular window, whereas the selectivity is less. Namely, filters designed using this window have wider transition region than those designed using the rectangular window. As a result, it is necessary to have a higher order filter in order to keep the same tansition region as that of the filters designed with the rectangular window. This is the price to pay for producing the higher attenuation.

This function also represents a kind of compromise between requirements for as narrow transition region as possible and as higher stopband attenuation as possible, where the transition region is considered more important characteristic.

One of the advantages of designing filter using the triangular window is the simplicity of computing coefficients.

The triangular window coefficients can be expressed as:

Figure 2-3-4 illustrates coefficients in the time-domain.

 

Figure 2-3-4. Triangular window coefficients in the time-domain

Figure 2-3-5. illustrates the coefficients spectrum of the triangular window shown in Figure 2-3-4.

 

Figure 2-3-5. Triangular (Bartlett) window in the frequency domain (spectrum)

The attenuation of triangular window is low for most digital filter applications, but it is considerably higher than that for rectangular window. In some cases, when high attenuations are not needed, this filter can be used because it provides an easy way of computing coefficients.

2.3.3 Hann Window

The Hann window is used to lessen bad effects on frequency characteristic produced by the final samples of a signal being filtered. Digital filters designed with this window have higher stopband attenuation than those designed with triangle function. The first side lobe in the frequency domain of this filter has 31dB attenuation, whereas it amounts to 44dB in the designed filter. The transition region is the same as for triangular window, which makes this function one of the most desirable for designing.

Another advantage of this window is the ability to realtively fast increase the stopband attenuation of the following lobes. Already the second lobe has 41dB attenuation, whereas it amounts to 54dB for the designed filter. Refer to Figure 2-3-7 illustrating the coefficients of the Hann window.

The Hann window belongs to a class of generalized cosine windows which will be discussed in more details at the end of this chapter.

The Hann window coefficients can be expressed as:

Figure 2-3-6. illustrates the Hann window coefficients in the time domain.

 

Figure 2-3-6. The Hann window coefficients in the time domain

 

 

 

 

Figure 2-3-7. The Hann window coefficients in the frequency domain

As seen from the table 2-3-1, the transition region of Hann window is wider than that of triangular window. The difference is that the transition region of triangular window is computed in terms of -26dB attenuation, and in terms of -31dB attenuation for Hann window Accordingly, the conclusion is that Hann window has sharper fall than triangular one, which is considered as its advantage.

For the same requirements for minimum attenuation, the Hann window will have a narrower transition region.

2.3.4 Bartlett-Hanning Window

The Bartlett-Hannign window is another compromise between requirements for as narrow transition region as possible and as higher stopband attenuation as possible. The stopband attenuation of a filter designed with this window amounts to 39dB which is not at all a large value.

The Bartlett-Hanning window coefficients are expressed as:

This window is in fact a combination of triangular (Bartlett) and Hann window and has higher minimum stopband attenuation than both of them. Considering that the transition region is almost the same as for triangular and Hann window, this function is one of most commonly used windows.

Figure 2-3-8. illustrates the Bartlett-Hanning window coefficients in the time domain.

 

Figure 2-3-8. The Bartlett-Hanning window coefficients in the time domain

 

 

 

 

Figure 2-3-9. The Bartlett-Hanning window coefficients in the frequency domain

When the stopband attenuation doesn’t need to be higher than 39dB, the Bartlett-Hanning window is one of the best solutions to use. As seen in Figure 2-3-9, the side lobes increase attenuation, which is one of very desirable characteristics of digital filters.

2.3.5 Hamming Window

The Hamming window is one of the most popular and most commonly used windows. A filter designed with the Hamming window has minimum stopband attenuation of 53dB, which is sufficient for most implementations of digital filters. The transition region is somewhat wider than that of the Hann and Bartlett-Hanning windows, whereas the stopband attenuation is considerably higher. Unlike minimum stopband attenuation, the transition region can be changed by changing the filter order. The transition region narrows, whereas the minimum stopband attenuation remains unchanged as the filter order increases.

The Hamming window coefficients are expressed as:

The Hamming window belongs to a class of generalized cosine functions which are described in more details at the end of this chapter.

Figure 2-3-10 illustrates the Hamming window coefficients in the time domain.

 

Figure 2-3-10. The Hamming window coefficients in the time domain

 

 

 

 

Figure 2-3-11. The Hamming window coefficients in the frequency domain

Figure 2-3-11 illustrates the Hamming window in the frequency domain. As seen, the first side lobe is attenuated, so that the minimum stopband attenuation is defined in terms of the second side lobe and amounts to 41dB. All side lobes have almost the same maximum values (about -45dB).

2.3.6 Bohman Window

The Bohman window is a convolution of two semi-periods of a cosine function. The transition region and the main lobe are wider than those for Hamming window, but the stopband attenuation is higher, therefore. The attenuation of the first side lobe for Bohman window is 46dB, whereas the filters designed with Bohman window have the stopband attenuation of 51dB.

The Bohman window coefficients are expressed as:

Figure 2-3-12 illustrates the Bohman window coefficients in the time domain, whereas Figure 2-3-13 illustrates its coefficients in the frequency domain.

 

Figure 2-3-12. The Bohman window coefficients in the time domain

 

 

 

 

Figure 2-3-13. The Bohman window coefficients in the frequency domain

Figure 2-3-13 illustrates the Bohman window coefficients in the frequency domain. As seen, the first side lobe has minimum attenuation of 46dB, whereas for designed filter it amounts to 51dB. The attenuation increases relatively fast. The second side lobe in the Bohman window frequency domain has the attenuation of 61dB, whereas for the filters designed with this window it amounts to 65dB. It should be noted that side lobes of such filters are different than shown in Figure 2-3-13.

With regard to minimum attenuation as well as to mid-wide transition region, it can be concluded that Bohman window is suitable for most applications.

2.3.7 Blackman Window

The Blackman window is, along with Kaiser, Hamming and Blackman-Harris windows, considered most commonly used and the most popular windows. Relatively high attenuation makes this window very convenient for almost all applications. The minimum stopband attenuation of a filter designed with this window amounts to 75dB.

The Blackman window coefficients are expressed as:

Figure 2-3-14 illustrates the Blackman window coefficients in the time domain, whereas Figure 2-3-15. illustrates its coefficients in the frequency domain.

 

Figure 2-3-14. The Blackman window coefficients in the time domain

 

 

 

 

Figure 2-3-15. The Blackman window coefficients in the frequency domain

As seen from Figure 2-3-15, the Blackman window frequency domain reminds of the Hann window frequency domain. The difference is in attenuation of the first side lobe which amounts to 51dB, as well as in the main lobe which is somewhat wider. The side lobes, following the first one, cause additional stopband attenuation.

2.3.8 Blackman-Harris Window

The Blackman-Harris window is definately one of the most well-known and most commonly used windows. It is characterized by high stopband attenuation and the widest transition region comparing to all windows mentioned in this chapter. However, increase in filter order (more complex filter) cannot affect the minimum stopband attenuation, but affects the transition region.

The Blackman-Harris window has almost twice as wide transition region than, say, the Hamming window. Such a drawback (wide transition region) can be overcome by increasing the filter order. The result is a higher order filter (comparing to one designed with Hamming window) with twice as high stopband attenuation. It should be noted that the transition region of the Hamming window ranges between − 3dB and − 41dB (decrease of 38dB), whereas for Blackman-Harris window it is decreased by 88dB (from − 3dB to − 91dB ).

The Blackman-Harris window has minimum stopband attenuation of 91dB, whereas for the filters designed with this window it amounts to 109dB. Such an attenuation is sufficient for any digital filter application. If it is possible to support a filter order that will be required by this window, then the Blackman-Harris window is probably the best soultion.

The Blackman-Harris window coefficients are expressed as:

Figure 2-3-16. illustrates the Blackman-Harris window coefficients in the time domain, whereas Figure 2-3-16. illustrates its coefficients in the frequency domain.

 

Figure 2-3-16. The Blackman-Harris window coefficients in the time domain

 

 

 

 

Figure 2-3-17. The Blackman-Harris window coefficients in the frequency domain

Figure 2-3-17. illustrates the main characteristics of the Blackman-Harris window in the frequency domain. As seen, the main lobe is wide and the first side lobe is suppressed. Minimum stopband attenuation is determined by the second side lobe having the minimum attenuation of 91dB. The attenuation of other side lobes gradually increases.

2.3.9 Blackman-Harris Window

The generalized cosine functions are a type of window functions whose coefficients can be obtained via expression:

There are some window functions that also belong to this class. These are:
 

• • Rectangular window;

 

• • Hann window;

 

• • Hamming window; and

 

• • Blackman window.

Each of these window functions is only a variation of the expression above. Their coefficients a, b and c are given in the table 2-3-3 below. 

WINDOW FUNCTION	A	B	C
Rectangular	1	0	0
Hann	0.5	0.5	0
Hamming	0.54	0.46	0
Blackman	0.42	0.5	0.08

  

Table 2-3-3. The coefficients of generalized cosine window functions

 

2.3.10 Kaiser Window

As you know, each of the windows described above is a kind of compromise between requirements for as narrow transition region as possible (greater selectivity) and as higher stopband attenuation as possible.

Comparing Hann and Bartlett-Hanning windows, it is obvious that both of them have the same transition region, but the Bartlett-Hanning window has higher attenuation. There is one more thing of concern which says that the minimum stopband attenuation depends on the specified window, whereas an increase in filter order affects the transition region.

All this leads us to the conclusion that the windows described here are not optimal. An optimal window is a function that has maximum attenuation according to the given width of the main lobe. The optimal window is also known as Kaiser window.

Its coefficients are expressed as:

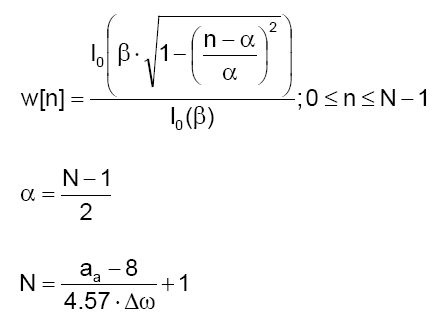
where aa is the minimum stopband attenuation, and Δ ω is the width of (normalized) transition region. The order of band-pass and band-stop filters, obtained from the expression above, should be multiplied by 2.

The value of parameter β can be obtained from the table 2-3-4. 

AA	Β
less than 21	0
between 21 and 50	0.5842(aa - 21)^0.4 + 0.07886(aa - 21)
more than 50	0.1102(aa - 8.7)

Table 2-3-4. Values of parameter β

I0(*) is a modified zero order Bessel function of the first kind. It can be approximated via expression:

In most practical cases it is sufficient to consider the first 20 elements of this order.

As can be seen from all mentioned above, in order to design an optimal Kaiser filter it is necessary to know normalized width of transition region as well as minimum desirable stopband attenuation.

Example:

What would a filter design with Kaiser window look like if we take into consideration the requirements given at the beginning of this chapter? The result of a filter designed with the Hann window is a 16th order filter.

Assuming that it is required to design a filter with the following characteristics:
 

1. 1. Minimum stopband attenuation is 40dB (aa);

 

1. 1. Transition region is between 2KHz and 3KHz (f1, f2); and

 

1. 1. Sampling frequency is 10KHz (fs).

Transition region:

The specified filter order is N=12. It means that the needed filter order is less by 4 than that obtained with the Hann window.

It is important to say that all the expressions above are obtained in an empirical way, which means that there will be some exceptions and variations in practice. For example, the expression used to compute the filter order gives accurate results in approximately 98% cases. Otherwise, the resulting filter order should be changed. Fortunately, the changes to be made are slight, and the filter order is increased or decreased by 2 at most.