Codeforces Round #746 (Div. 2)
A Gamer Hemose
题目
你有 \(n\) 种武器,每种武器使用一次可以造成 \(a_i\) 的伤害,并且同一种武器不能连续用两次(但是可以重复使用)。现在有一个 HP 为 \(H\) 的遗迹守卫,问你最少多少次A掉它。
思路
显然
代码
#include <iostream>
#include <cstdio>
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return negt ? -re : re;
}
template <char l , char r>
char readc() {
char c = getchar();
while(c < l || c > r)c = getchar();
return c;
}
#define int long long
void solve() {
int n , d1 = 0 , d2 = 0 , h;
n = read() , h = read();
for(int i = 1 ; i <= n ; i++) {
int d = read();
if(d > d1)d2 = d1 , d1 = d;
else if(d > d2) d2 = d;
}
int ans = h / (d1 + d2) * 2;
h %= (d1 + d2);
if(h != 0)
ans += (h > d1 ? 2 : 1);
printf("%lld\n" , ans);
}
signed main() {
int T = read();
while(T--)solve();
return 0;
}
B Hemose Shopping
题目
给你两个数 \(n, x\),代表有 \(n\) 个元素。
然后输入 \(n\) 个元素。
现在问你,能否通过交换两个距离大于等于 \(x\) 的数,使得数组可以按照非递减的顺序来排序。
如果可以,输出 YES,否则,输出 NO。
注:\(a\) 和 \(b\) 的距离是:\( \lvert a - b \rvert\)
思路
首先,明白一个事情:设三元组\((x,y,z)\),我们假设\(x,y\)不能互换,\(x,z\)和\(y,x\)之间可以互换,则\((x,y,z)\to(z,y,x)\to(z,x,y)\to (y,x,z)\)相当于\(x,y\)可以互换.
首先,我们求出一个\(l\),使得\(\forall i\in[1,l]\),\(a_i\)和\(a_n\)可以互换.
再求出一个\(r\),使得,\(\forall i\in[r,n]\),\(a_i\)和\(a_1\)可以互换.
则相当于\([1,l]\),\([r,n]\)内的数两两可以互换,\([l+1,r-1]\)内的数不能和任何一个数互换.
所以,若两个区间有交集,相当于全序列可以两两交换.
中间不能换的部分必须和排序后的数组一致.
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return negt ? -re : re;
}
template <char l , char r>
char readc() {
char c = getchar();
while(c < l || c > r)c = getchar();
return c;
}
const int N = 1e5 + 10;
int n , x;
int a[N] , b[N];
void solve() {
n = read() , x = read();
for(int i = 1 ; i <= n ; i++)
b[i] = a[i] = read();
sort(b + 1 , b + n + 1);
int l = n - x , r = x + 1;
// if(l >= r)puts("YES");
for(int i = l + 1 ; i < r ; i++)
if(a[i] != b[i]) {
puts("NO");
return;
}
puts("YES");
}
int main() {
int T = read();
while(T--)solve();
return 0;
}
C Bakry and Partitioning
题目
一棵树有 \(n\) 个节点,第 \(i\) 个节点的点权为 \(a_i\) 。(注:树是一个有 \(n\) 个节点、\(n-1\) 条边的连通图)
你需要回答:能不能选择这棵树中的至少 \(1\) 条边、至多 \(k-1\) 条边删除,使得删除完这些边的树满足以下条件:
- 每个联通块的点权异或和相等
思路
首先,若最后有解,一定有一种划分方案,使得最后连通块的数量不超过\(3\).
证明:三个点权异或和相同的连通块合并后得到新连通块,新连通块的点权异或和不变,\(x\oplus x\oplus x=0\oplus x=x\).因此,我们可以每次减少两个连通块至连通块的数量等于3或等于2.
所以,情况就剩下以下三种(设\(a\)为全树点权的异或和):
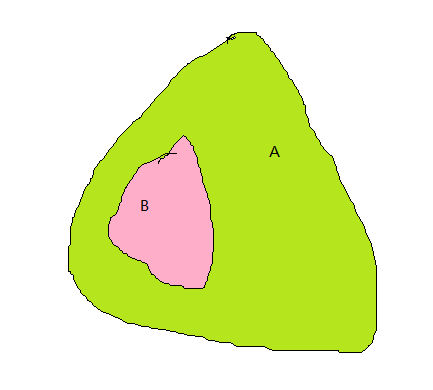
A为全树,B为子树,分为B以及B以外两个连通块,点权异或和分别为\(b,a\oplus b\).
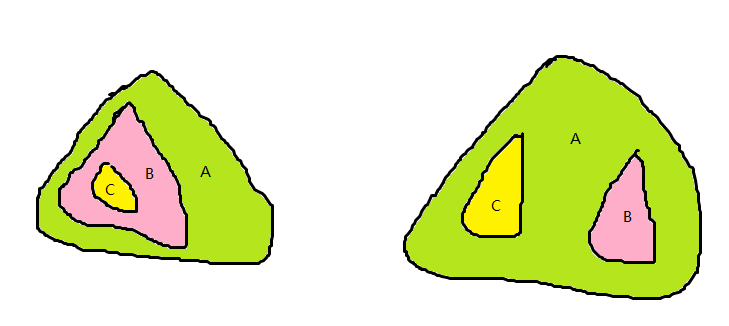
同理,两图分别有\(a\oplus b=b\oplus c=c\)和\(a\oplus b\oplus c=b=c\),分别解得\(b=0,a=c\)和\(a=b=c\).
代码
#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return negt ? -re : re;
}
template <char l , char r>
char readc() {
char c = getchar();
while(c < l || c > r)c = getchar();
return c;
}
const int N = 1e5 + 10;
struct Edge {
int to , nxt;
} ed[N * 2];
int head[N];
int edg_cnt;
void addedge(int u , int v) {
int cnt = ++edg_cnt;
ed[cnt].to = v , ed[cnt].nxt = head[u] , head[u] = cnt;
}
int n , k;
int sum;
int a[N];
bool ans;
using pr = pair<bool , int>;
pr dfs(int x , int fa) {//返回值第一维表示当前子树有(true)/无(false)和全树点权异或和相同的子树,第二位表示当前子树的点权异或和.
pr res = (pr) {false , a[x]};
for(int i = head[x] ; i ; i = ed[i].nxt) {
int to = ed[i].to;
if(to == fa)continue;
pr tmp = dfs(to , x);
if(tmp.first && res.first)ans = true;
res.first |= tmp.first , res.second ^= tmp.second;
}
ans |= res.first && (res.second == 0);
res.first |= (res.second == sum);
return res;
}
void solve() {
n = read() , k = read();
edg_cnt = 0;
sum = 0;
for(int i = 1 ; i <= n ; i++)
head[i] = 0;
for(int i = 0 ; i <= n * 2 ; i++)
ed[i].to = ed[i].nxt = 0;
for(int i = 1 ; i <= n ; i++)
sum ^= (a[i] = read());
for(int i = 1 ; i < n ; i++) {
int u = read() , v = read();
addedge(u , v) , addedge(v , u);
}
if(sum == 0) {
puts("YES");
return ;
}
if(k == 2) {
puts("NO");
return ;
}
ans = false;
dfs(1 , 0);
puts(ans ? "YES" : "NO");
}
int main() {
int T = read();
while(T--)solve();
return 0;
}
D Hemose in ICPC ?
题目
给一棵 \(n\) 个点的树,定义 \(Dist(u,v)\) 为 \(u \to v\) 路径上的边构成的边权集合的 \(\gcd\),且 \(u \neq v\)。
每一你可以询问交互库 \(x\) 个点的点集 \(X\),交互库会返回 \(X\) 中,\(\max\{Dist(u,v)\}, u,v \in X\) 。也就是说,交互库会找到 \(X\) 中 \(Dist\) 最大的一个点对 \((u,v)\) 并且返回它们的 \(Dist\)。
最多可以询问交互库 \(12\) 次。你需要找到整棵树中 \(Dist(u,v)\) 最大的那个点对 \((u,v)\)。若有多个,任意一个都合法。
思路
首先一点,交互器回答\(\gcd\)和回答\(\max\)无异.
然后一点,
最多可以询问交互库 \(12\) 次
赤裸裸的\(\log n\).
直接二分即可.
然后就是如何将树均匀分为联通的两部分,其实欧拉序(父->子树->父->子树->父的顺序)可以实现.
代码
#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
int read() {
int re = 0;
char c = getchar();
bool negt = false;
while(c < '0' || c > '9')
negt |= (c == '-') , c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return negt ? -re : re;
}
template <char l , char r>
char readc() {
char c = getchar();
while(c < l || c > r)c = getchar();
return c;
}
const int N = 1e3 + 10;
struct Edge {
int to , nxt;
} ed[N * 2];
int head[N];
void addedge(int u , int v) {
static int cnt = 0;
++cnt;
ed[cnt].to = v , ed[cnt].nxt = head[u] , head[u] = cnt;
}
int n;
int id[N * 2];
void dfs(int x , int fa) {
static int cnt = 0;
id[++cnt] = x;
for(int i = head[x] ; i ; i = ed[i].nxt) {
int to = ed[i].to;
if(to == fa)continue;
dfs(to , x);
id[++cnt] = x;
}
}
int ask(vector<int> &node) {
cout << '?' << ' ' << node.size() << ' ';
for(int i : node)
cout << i << ' ';
cout << endl;
node.clear();
int res;
cin >> res;
return res;
}
vector<int> node;
void add(int l , int r) {
static bool vis[N];
memset(vis , 0 , sizeof(vis));
for(int i = l ; i <= r ; i++)
if(!vis[id[i]]) {
vis[id[i]] = true;
node.push_back(id[i]);
}
}
int main() {
ios::sync_with_stdio(false);
cin >> n;
for(int i = 1 ; i < n ; i++) {
int u , v;
cin >> u >> v;
addedge(u , v) , addedge(v , u);
}
for(int i = 1 ; i <= n ; i++)node.push_back(i);
int maxVal = ask(node);
dfs(1 , 0);
int l = 1 , r = n * 2 - 1;
while(l + 1 < r) {
int mid = (l + r) / 2;
add(l , mid);
if(ask(node) == maxVal) r = mid;
else l = mid;
}
cout << "! " << id[l] << ' ' << id[r] << endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号