「字符串算法」第5章 AC自动机课堂过关
「字符串算法」第5章 AC自动机课堂过关
洛谷模板题
P3808 【模板】AC自动机(简单版)
题目
题目描述
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。输入格式
第一行是一个整数,表示模式串的个数 \(n\)。
第 \(2\) 到第 \((n + 1)\) 行,每行一个字符串,第 \((i + 1)\) 行的字符串表示编号为 \(i\) 的模式串 \(s_i\)。
最后一行是一个字符串,表示文本串 \(t\)。输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1
3 a aa aa aaa输出 #1
3输入 #2
4 a ab ac abc abcd输出 #2
3输入 #3
2 a aa aa输出 #3
2
说明/提示
样例 1 解释
\(s_2\) 与 \(s_3\) 编号(下标)不同,因此各自对答案产生了一次贡献。
样例 2 解释
\(s_1\),\(s_2\),\(s_4\) 都在串
abcd里出现过。数据规模与约定
- 对于 \(50\%\) 的数据,保证 \(n = 1\)。
- 对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 10^6\),\(1 \leq |t| \leq 10^6\),\(1 \leq \sum\limits_{i = 1}^n |s_i| \leq 10^6\)。
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 1500010
using namespace std;
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(fail , 0 , sizeof(fail));
memset(end , 0 , sizeof(end));
cnt = 1;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int key = s[i] - 'a';
if(trie[p][key] == 0)
trie[p][key] = ++cnt;
p = trie[p][key];
}
end[p]++;
return p;
}
void kmp() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = 1;
q.push(root);
fail[root] = 0;
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
q.push(trie[p][i]);
fail[trie[p][i]] = trie[fail[p]][i];
}
}
}
}
int query(char *s) {
int len = strlen(s);
int ans = 0;
int p = root;
for(int i = 0 ; i < len ; i++) {
int key = s[i] - 'a';
int k = trie[p][key];
while(k > 1 && ~end[k]) {//注意这里的优化,否则被"aaa..."的数据卡掉
ans += end[k];
end[k] = -1;
k = fail[k];
}
p = trie[p][key];
}
return ans;
}
} AC;
char s[1000010];
int n;
int main() {
int T = 1;
while(T--) {
AC.clear();
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++)
scanf("%s" , s) , AC.insert(s);
AC.kmp();
scanf("%s" , s);
printf("%d\n" , AC.query(s));
}
return 0;
}
P5357 【模板】AC自动机(二次加强版)
题目
题目描述
给你一个文本串 \(S\) 和 \(n\) 个模式串 \(T_{1..n}\),请你分别求出每个模式串 \(T_i\) 在 \(S\) 中出现的次数。
输入格式
第一行包含一个正整数 \(n\) 表示模式串的个数。
接下来 \(n\) 行,第 \(i\)行包含一个由小写英文字母构成的字符串 \(T_i\)。
最后一行包含一个由小写英文字母构成的字符串 \(S\)。
数据不保证任意两个模式串不相同。
输出格式
输出包含 \(n\) 行,其中第 \(i\) 行包含一个非负整数表示 \(T_i\) 在 \(S\) 中出现的次数。
输入输出样例
输入 #1
5 a bb aa abaa abaaa abaaabaa输出 #1
6 0 3 2 1说明/提示
\(1\le n\le 2\times10^5\),\(T_{1..n}\) 的长度总和不超过 \(2\times 10^5\),\(S\) 的长度不超过 \(2\times10^6\)。
思路
为什么把这道题放到前面呢?简单啊
想想可以知道上面那题的优化在这里不管用.
再想一下,搜索文章时,每遍历一个字符就要向上跳fail指针,同一个结点,更新的其他点都是固定的,那么我们是否可以考虑像线段树一样用懒标记维护呢?答案显然是肯定的(不然我就不会说),最后把所有懒标记"上传"(毕竟fail指向的时深度更小的结点嘛),这题就解决了.
又考虑到fail指向深度更小的结点,所以"上传"的时候要按照深度从大到小的顺序.
这题的这个思想非常重要,下面很多题都是用类似懒标记的方法完成的!
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 200010
using namespace std;
bool vis[N];
int q[N * 27] , h , t;//开27倍
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int tag[N];//其实tag和dat可以合二为一,但是为了好看就分开了
int dat[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(end , 0 , sizeof(end));
memset(fail , 0 , sizeof(fail));
memset(tag , 0 , sizeof(tag));
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
if(trie[p][c] == 0)
trie[p][c] = ++cnt;
p = trie[p][c];
}
++end[p];
return p;
}
void build() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0) trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
q.push(trie[p][i]);
}
}
}
}
void article(char *s) {
int len = strlen(s);
int p = root;
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
p = trie[p][c];
++tag[p];
++dat[p];
}
}
void spread() {
q[t++] = root;
while(h < t) {
vis[q[h]] = true;
int p = q[h];
for(int i = 0 ; i < 26 ; i++)
if(vis[trie[p][i]] == false && trie[p][i] != 0)
q[t++] = trie[p][i];
h++;
}
for( ; t >= 0 ; t--) {
int tmp = q[t];
tag[fail[tmp]] += tag[tmp];
dat[fail[tmp]] += tag[tmp];
tag[tmp] = 0;
}
return;
}
}AC;
char s[2000010];
int n;
int id[N];
int main() {
AC.clear();
cin >> n;
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s);
id[i] = AC.insert(s);
}
scanf("%s" , s);
AC.build();
AC.article(s);
AC.spread();
for(int i = 1 ; i <= n ; i++) {
printf("%d\n" , AC.dat[id[i]]);
}
return 0;
}
P3796 【模板】AC自动机(加强版)
题目
题目描述
有 \(N\) 个由小写字母组成的模式串以及一个文本串 \(T\)。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串 \(T\) 中出现的次数最多。
输入格式
输入含多组数据。保证输入数据不超过 \(50\) 组。
每组数据的第一行为一个正整数 \(N\),表示共有 \(N\) 个模式串,\(1 \leq N \leq 150\)。
接下去 \(N\) 行,每行一个长度小于等于 \(70\) 的模式串。下一行是一个长度小于等于 \(10^6\) 的文本串 \(T\)。保证不存在两个相同的模式串。
输入结束标志为 \(N=0\)。
输出格式
对于每组数据,第一行输出模式串最多出现的次数,接下去若干行每行输出一个出现次数最多的模式串,按输入顺序排列。
输入输出样例
输入 #1
2 aba bab ababababac 6 beta alpha haha delta dede tata dedeltalphahahahototatalpha 0输出 #1
4 aba 2 alpha haha
思路
上面那题写出来了,这题还难吗?
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 10510
using namespace std;
bool vis[N];
int q[N * 27] , h , t;
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int tag[N];
int dat[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(end , 0 , sizeof(end));
memset(fail , 0 , sizeof(fail));
memset(tag , 0 , sizeof(tag));
memset(q , 0 , sizeof(q));
memset(vis , 0 , sizeof(vis));
memset(dat , 0 , sizeof(dat));
h = t = 0;
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
if(trie[p][c] == 0)
trie[p][c] = ++cnt;
p = trie[p][c];
}
++end[p];
return p;
}
void build() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0) trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
q.push(trie[p][i]);
}
}
}
}
void article(char *s) {
int len = strlen(s);
int p = root;
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
p = trie[p][c];
++tag[p];
++dat[p];
}
}
void spread() {
q[t++] = root;
while(h < t) {
vis[q[h]] = true;
int p = q[h];
for(int i = 0 ; i < 26 ; i++)
if(vis[trie[p][i]] == false && trie[p][i] != 0)
q[t++] = trie[p][i];
h++;
}
for( ; t >= 0 ; t--) {
int tmp = q[t];
tag[fail[tmp]] += tag[tmp];
dat[fail[tmp]] += tag[tmp];
tag[tmp] = 0;
}
return;
}
}AC;
char s[160][80];
char txt[2000010];
int n;
int id[N];
int main() {
while(true) {
memset(s , 0 , sizeof(s));
memset(txt , 0 , sizeof(txt));
memset(id , 0 , sizeof(id));
AC.clear();
scanf("%d" , &n);
if(n == 0)
break;
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s[i]);
id[i] = AC.insert(s[i]);
}
AC.build();
scanf("%s" , txt);
AC.article(txt);
AC.spread();
int ans = 0;
for(int i = 1 ; i <= n ; i++)
if(ans < AC.dat[id[i]])
ans = AC.dat[id[i]];
printf("%d\n" , ans);
for(int i = 1 ; i <= n ; i++) {
if(AC.dat[id[i]] == ans)
puts(s[i]);
}
}
return 0;
}
A. 【例题1】单词查询
前三题都比较简单,不再讲解
题目

code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 1000010
using namespace std;
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(fail , 0 , sizeof(fail));
memset(end , 0 , sizeof(end));
cnt = 1;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int key = s[i] - 'a';
if(trie[p][key] == 0)
trie[p][key] = ++cnt;
p = trie[p][key];
}
end[p]++;
return p;
}
void kmp() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = 1;
q.push(root);
fail[root] = 0;
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
q.push(trie[p][i]);
fail[trie[p][i]] = trie[fail[p]][i];
}
}
}
}
int query(char *s) {
int len = strlen(s);
int ans = 0;
int p = root;
for(int i = 0 ; i < len ; i++) {
int key = s[i] - 'a';
int k = trie[p][key];
while(k > 1) {
ans += end[k];
end[k] = 0;
k = fail[k];
}
p = trie[p][key];
}
return ans;
}
} AC;
char s[1000010];
int n;
int main() {
int T = 1;
cin >> T;
while(T--) {
AC.clear();
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++)
scanf("%s" , s) , AC.insert(s);
AC.kmp();
scanf("%s" , s);
printf("%d\n" , AC.query(s));
}
return 0;
}
B. 【例题2】单词频率
题目
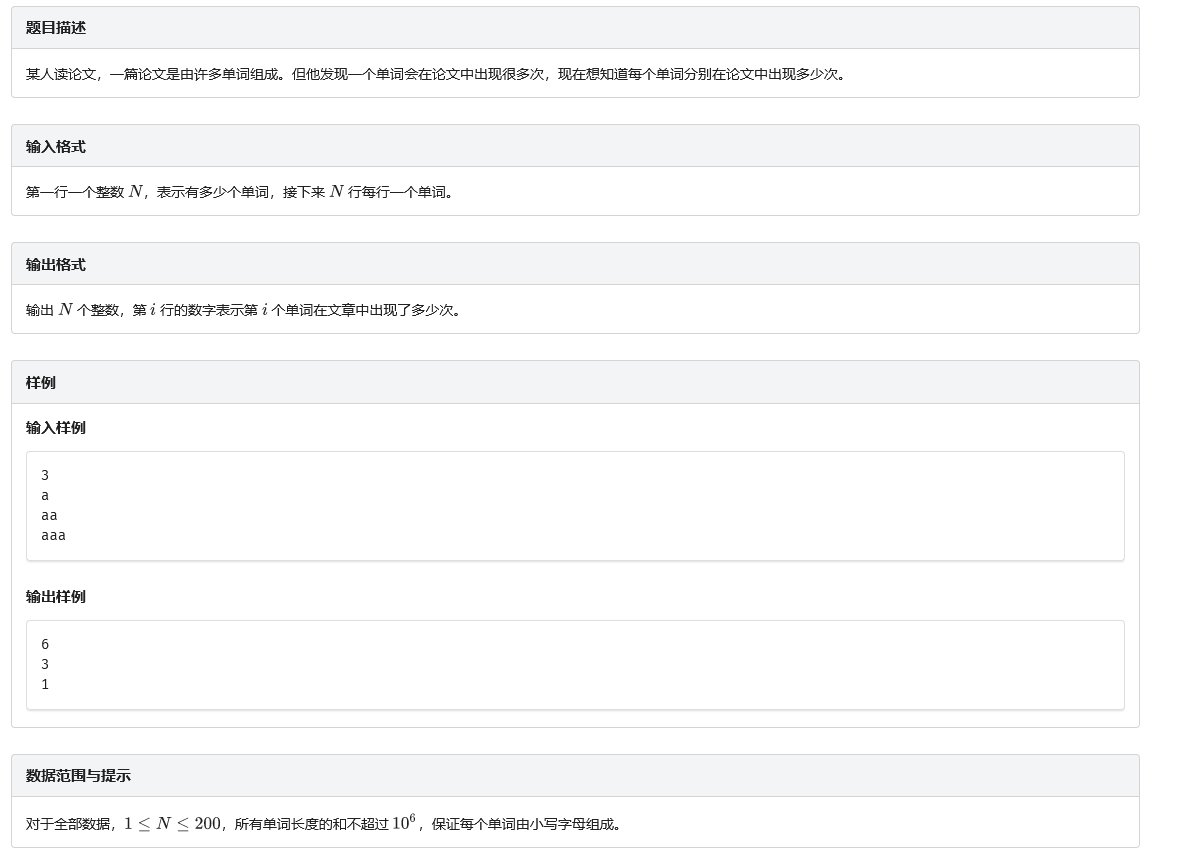
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <queue>
#define N 1000010
using namespace std;
bool vis[N];
int q[N * 27] , h , t;
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int tag[N];
int dat[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(end , 0 , sizeof(end));
memset(fail , 0 , sizeof(fail));
memset(tag , 0 , sizeof(tag));
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
if(trie[p][c] == 0)
trie[p][c] = ++cnt;
p = trie[p][c];
}
++end[p];
return p;
}
void build() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0) trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
q.push(trie[p][i]);
}
}
}
}
void article(char *s) {
int len = strlen(s);
int p = root;
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'a';
p = trie[p][c];
++tag[p];
++dat[p];
/* int k = p;
while(k > 1) {
++dat[k];
k = fail[k];
}//*/
}
}
void spread() {
q[t++] = root;
while(h < t) {
vis[q[h]] = true;
int p = q[h];
for(int i = 0 ; i < 26 ; i++)
if(vis[trie[p][i]] == false && trie[p][i] != 0)
q[t++] = trie[p][i];
h++;
}
for( ; t >= 0 ; t--) {
int tmp = q[t];
tag[fail[tmp]] += tag[tmp];
dat[fail[tmp]] += tag[tmp];
tag[tmp] = 0;
}
return;
/*
vis[x] = true;
for(int i = 0 ; i < 26 ; i++) {
if(vis[trie[x][i]] == false && trie[x][i] != 0) {
spread(trie[x][i]);
}
}
tag[fail[x]] += tag[x];
dat[fail[x]] += tag[x];
tag[x] = 0;//*/
}
}AC;
char s[2000010];
string txt;
int n;
int id[N];
int main() {
AC.clear();
cin >> n;
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s);
id[i] = AC.insert(s);
AC.article(s);
}
AC.build();
AC.spread();
for(int i = 1 ; i <= n ; i++) {
printf("%d\n" , AC.dat[id[i]]);
}
// cout << AC.cnt << endl <<
return 0;
}
C. 【例题3】前缀匹配
题目

code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 1000010
using namespace std;
bool vis[N];
int q[N * 27] , h , t;
struct ACauto {
#define root 1
int trie[N][27];
int end[N];
int fail[N];
int tag[N];
int dat[N];
int ans[N];
int dep[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(end , 0 , sizeof(end));
memset(fail , 0 , sizeof(fail));
memset(tag , 0 , sizeof(tag));
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'A';
if(trie[p][c] == 0)
trie[p][c] = ++cnt;
dep[trie[p][c]] = dep[p] + 1,
p = trie[p][c];
}
end[p] = true;
return p;
}
void build() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
q.push(trie[p][i]);
}
}
}
}
void article(char *s) {
int len = strlen(s);
int p = root;
for(int i = 0 ; i < len ; i++) {
int c = s[i] - 'A';
p = trie[p][c];
tag[p] = true;
dat[p] = true;
}
}
void spread() {
q[t++] = root;
while(h < t) {
vis[q[h]] = true;
int p = q[h];
for(int i = 0 ; i < 26 ; i++)
if(vis[trie[p][i]] == false && trie[p][i] != 0)
q[t++] = trie[p][i];
h++;
}
for( ; t >= 0 ; t--) {
int tmp = q[t];
tag[fail[tmp]] = (tag[fail[tmp]] || tag[tmp]);
dat[fail[tmp]] = (dat[fail[tmp]] || tag[tmp]);
tag[tmp] = false;
}
memset(vis , 0 , sizeof(vis));
dat[root] = tag[root] = 0;
dat[0] = 0;
return;
}
void GetAns(int p) {
vis[p] = true;
if(dat[p] && p > root)
ans[p] = dep[p];
for(int i = 0 ; i < 26 ; i++) {
int k = trie[p][i];
if(dep[k] <= dep[p]) continue;
if(!vis[k]) {
if(ans[k] < ans[p])
ans[k] = ans[p];
GetAns(k);
}
}
}
}AC;
char s[110];
char txt[10000010];
int n;
int id[N];
int main() {
AC.clear();
scanf("%d %d" , &n , &n);
scanf("%s" , txt);
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s);
id[i] = AC.insert(s);
}
AC.build();
AC.article(txt);
AC.spread();
AC.GetAns(root);
for(int i = 1 ; i <= n ; i++)
printf("%d\n" , AC.ans[id[i]]);
return 0;
}
D. 【例题4】屏蔽词删除
题目

思路
这题也不难
把屏蔽词放到AC自动机中,记录S的每个字符在跑AC自动机时的位置,不好描述,看代码:
int query(ChainNode &s) {
int ans = 0;
int p = root;
for(int i = s.next[0] ; ~i ; i = s.next[i]) {
int c = s.c[i] - 'a';
p = trie[p][c];
if(end[p] > 0) {//这里下面讲
for(int j = 1 ; j <= dep[p] ; j++) {
s.del(i);
i = s.from[i];
}
p = s.dat[i];
}
s.dat[i] = p;//这个东西
}
return ans;
}
如果碰到结束标记就把那一串单词删掉(这里用双向链表\(O(len)\)实现,\(len\)为屏蔽单词长度),从记录的位置(s.dat[i])继续跑AC自动机即可.
S串的每个字符基本只被访问一次,最多被删除一次,所以复杂度为\(O(|S|)\)
code
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 100010
#define S 1000010
using namespace std;
struct ChainNode {
int from[S] , next[S];
int dat[S];
char c[S];
void read() {
char tmp[S];
memset(tmp , 0 , sizeof(tmp));
scanf("%s" , tmp);
int len = strlen(tmp);
next[0] = 1;
for(int i = 1 ; i <= len ; i++)
c[i] = tmp[i - 1] ,
from[i] = i - 1 ,
next[i] = i + 1;
next[len] = -1;
}
void print() {
for(int i = next[0] ; ~i ; i = next[i])
putchar(c[i]);
putchar('\n');
}
void del(int x) {//删除下标为x的字符
next[from[x]] = next[x];
from[next[x]] = from[x];
}
}s;
struct ACauto {
#define root 1
int trie[N][27];
int dep[N];
int end[N];
int fail[N];
int cnt;
void clear() {
memset(trie , 0 , sizeof(trie));
memset(fail , 0 , sizeof(fail));
memset(end , 0 , sizeof(end));
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int key = s[i] - 'a';
if(trie[p][key] == 0)
trie[p][key] = ++cnt;
p = trie[p][key];
}
end[p]++;
dep[p] = len;
return p;
}
void kmp() {
queue <int> q;
for(int i = 0 ; i < 26 ; i++)
trie[0][i] = root;
q.push(root);
fail[root] = 0;
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i < 26 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
q.push(trie[p][i]);
fail[trie[p][i]] = trie[fail[p]][i];
}
}
}
}
int query(ChainNode &s) {
int ans = 0;
int p = root;
for(int i = s.next[0] ; ~i ; i = s.next[i]) {
int c = s.c[i] - 'a';
p = trie[p][c];
if(end[p] > 0) {
for(int j = 1 ; j <= dep[p] ; j++) {
s.del(i);
i = s.from[i];
}
p = s.dat[i];
}
s.dat[i] = p;
}
return ans;
}
} AC;
char t[100010];
int n;
int main() {
AC.clear();
s.read();
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++) {
memset(t , 0 , sizeof(t));
scanf("%s" , t) , AC.insert(t);
}
AC.kmp();
AC.query(s);
s.print();
return 0;
}
E. 【例题5】病毒代码
题目
题目描述
二进制病毒审查委员会最近发现了如下的规律:某些确定的二进制串是病毒的代码。如果某段代码中不存在任何一段病毒代码,那么我们就称这段代码是安全的。现在委员会已经找出了所有的病毒代码段,试问,是否存在一个无限长的安全的二进制代码。
示例:
例如如果 \(\{011, 11, 00000\}\) 为病毒代码段,那么一个可能的无限长安全代码就是 \(010101 \ldots\)。如果 \(\{01, 11, 000000\}\) 为病毒代码段,那么就不存在一个无限长的安全代码。
现在给出所有的病毒代码段,判断是否存在无限长的安全代码。
输入格式
第一行包括一个整数 \(n\),表示病毒代码段的数目。
以下的 \(n\) 行每一行都包括一个非空的 \(01\) 字符串,代表一个病毒代码段。
输出格式
如果存在无限长的安全代码,输出
TAK,否则输出NIE。输入输出样例
输入 #1
3 01 11 00000输出 #1
NIE说明/提示
\(1 \leq n \leq 2000\),所有病毒代码段的总长度不超过 \(3 \times 10^4\)。
思路
AC自动机的紫题怎么都这么简单
一个显然的结论:
如果001是不合法的,那么包含001的都是不合法的,如101001,00001.因此,我们求fail的时候,若001不合法(有结尾标记),则所有指向该'1'所在点的fail 所在的trie结点均打上标记.有点模糊,看代码:
void build() {
queue <int> q;
for(int i = 0 ; i <= 1 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i <= 1 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
tag[trie[p][i]] |= tag[trie[fail[p]][i]];//一般的AC自动机是不带这句的
q.push(trie[p][i]);
}
}
}
}
问题就转换为AC自动机上是否存在一个环,且该环包含的点均没有被打上标记.(这一步需要对AC自动机有较深的理解)
怎么判环?Tarjan呀!
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define N 30010
using namespace std;
bool ans;
int q[N * 2] , h , t;
struct ACauto {
#define root 1
int trie[N][2];
int fail[N];
bool tag[N];
int cnt;
int dfn[N] , low[N] , vis[N];
void clear() {
memset(trie , 0 , sizeof(trie));
memset(fail , 0 , sizeof(fail));
memset(tag , 0 , sizeof(tag));
memset(q , 0 , sizeof(q));
memset(vis , 0 , sizeof(vis));
h = t = 0;
cnt = root;
}
int insert(char *s) {
int p = root;
int len = strlen(s);
for(int i = 0 ; i < len ; i++) {
int c = s[i] - '0';
if(trie[p][c] == 0)
trie[p][c] = ++cnt;
p = trie[p][c];
}
tag[p] = true;
return p;
}
void build() {
queue <int> q;
for(int i = 0 ; i <= 1 ; i++)
trie[0][i] = root;
q.push(root);
while(!q.empty()) {
int p = q.front();
q.pop();
for(int i = 0 ; i <= 1 ; i++) {
if(trie[p][i] == 0)
trie[p][i] = trie[fail[p]][i];
else {
fail[trie[p][i]] = trie[fail[p]][i];
tag[trie[p][i]] |= tag[trie[fail[p]][i]];
q.push(trie[p][i]);
}
}
}
}
void Tarjan(int x) {
if(ans) return;
static int Time = 1;
dfn[x] = low[x] = Time;
for(int i = 0 ; i <= 1 ; i++) {
int to = trie[x][i];
if(tag[to]) continue;
if(dfn[to] == 0) {
Tarjan(to);
} else if(vis[to] == 0) {
ans = true;//如果不能理解这里,好好学学tarjan吧
}
}
vis[x] = true;
}
} AC;
char s[N];
int n;
int main() {
memset(s , 0 , sizeof(s));
AC.clear();
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s);
AC.insert(s);
}
AC.build();
AC.Tarjan(root);
puts(ans ? "TAK" : "NIE");
return 0;
}




