「数据结构」第2章 树状数组课堂过关
目录
「数据结构」第2章 树状数组课堂过关
A. 【例题1】单点修改区间查询
题目

代码
#include <iostream>
#include <cstdio>
using namespace std;
#define N 1000010
#define ll long long
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
struct node {
int siz;
ll a[N * 2];
#define lowbit(_) ((_) & -(_))
void add(int i , ll dat) {
for( ; i <= siz ; i += lowbit(i))
a[i] += dat;
}
ll getsum(int r) {
ll sum = 0;
for( ; r ; r -= lowbit(r))
sum += a[r];
return sum;
}
}tarray;
int n , q;
int main() {
n = read(); q = read();
tarray.siz = n;
for(int i = 1 ; i <= n ; i++)
tarray.add(i , read());
while(q--) {
int ty = read() , d1 = read() , d2 = read();
if(ty == 1)
tarray.add(d1 , d2);
else
printf("%lld\n" , tarray.getsum(d2) - tarray.getsum(d1 - 1));
}
return 0;
}
B. 【例题2】逆序对
题目
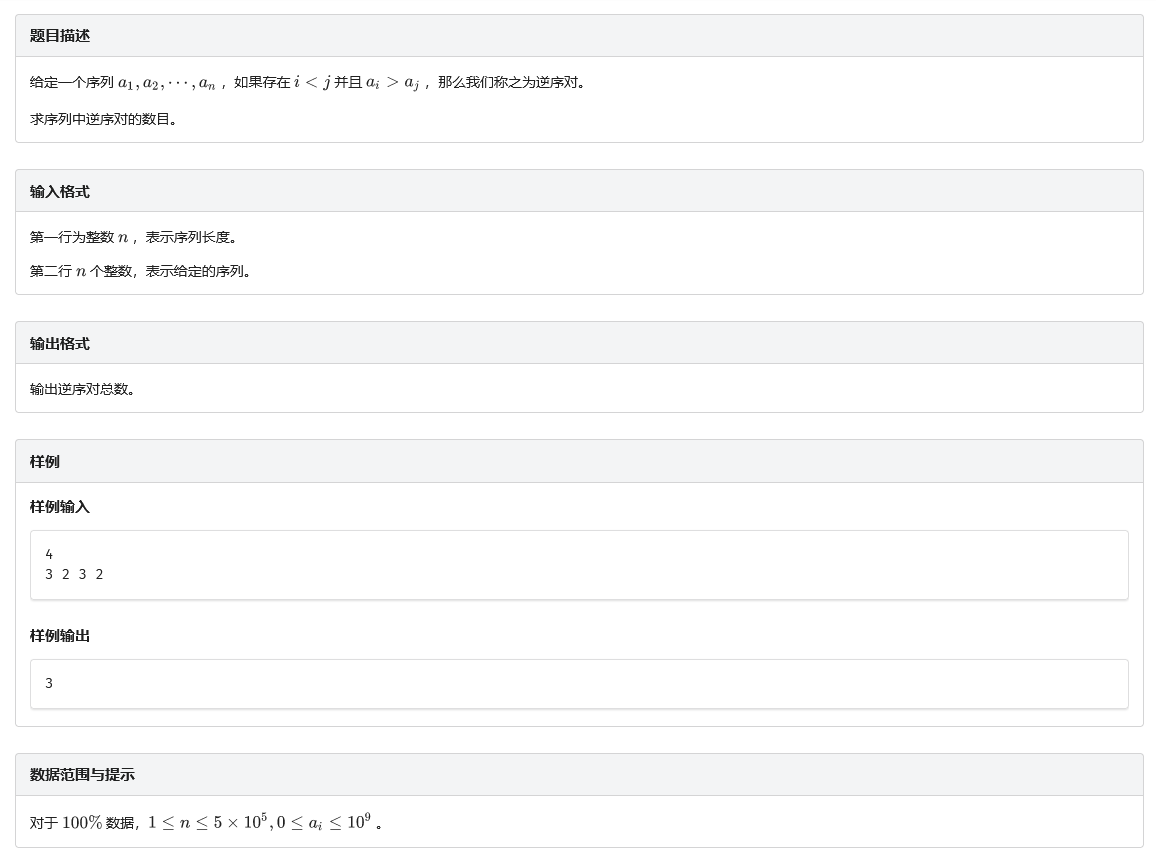
代码
模板题,不多解释
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define nn 500010
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
struct TreeArray {
int dat[nn * 2];
int siz;
#define lowbit(_) ((_) & -(_))
inline void updata(int d , int poi) {
for( ; poi <= siz ; poi += lowbit(poi))
dat[poi] += d;
}
inline int getsum(int r) {
int sum = 0;
for( ; r > 0 ; r -= lowbit(r))
sum += dat[r];
return sum;
}
}t;
struct node {
int id , dat;
};
bool cmp(node a , node b) {
return a.dat < b.dat;
}
node tmp[nn];
void Discretize(int *st , int *ed) {
int n = ed - st;
for(int i = 0 ; i < n ; i++)
tmp[i].id = i , tmp[i].dat = st[i];
sort(tmp , tmp + n , cmp);
int cnt = 1;
st[tmp[0].id] = cnt;
for(int i = 1 ; i < n ; i++) {
if(tmp[i].dat != tmp[i - 1].dat) ++cnt;
st[tmp[i].id] = cnt;
}
}
int a[nn];
int n;
int main() {
n = t.siz = read();
for(int i = 1 ; i <= n ; i++)
a[i] = read();
Discretize(a + 1 , a + n + 1);
long long ans = 0;
for(int i = n ; i >= 1 ; i--) {
ans += t.getsum(a[i] - 1);
t.updata(1 , a[i]);
}
cout << ans;
return 0;
}
C. 【例题3】严格上升子序列数
题目

思路&代码
是道好题
1
这题的DP并不难想,设\(f_{i,j}\)表示以\(i\)为结束点,长度为\(j\)的严格上升子序列的数量,则\(f_{i,1}=1\),答案为\(\sum^n_{i=1}f_{i,m}\)
状态转移:
\[f_{i,j}=\sum f_{k,j-1}(a_k < i\and k<i)
\]
写成代码:
memset(f , 0 , sizeof(f));
for(int i = 1 ; i <= n ; i++)
f[i][1] = 1;
for(int i = 1 ; i <= n ; i++)//这里先枚举i,j都是一样的
for(int j = 2 ; j <= m ; j++)
for(int k = 1 ; k < i ; k++)
if(a[k] < a[i])
f[i][j] += f[k][j - 1];
int ans = 0;
for(int i = 1 ; i <= n ; i++)
ans += f[i][m];
时间为\(O(n^2m)\)
2
考虑优化
按照逆序对的思想,将\(a\)离散化后,从1到\(n\)枚举,\(a_i\)做\(f\)的下标,就可以不用判断\(a_k < a_i\),为嵌入数据结构打下基础
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 1010
#define ll long long
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
struct node {
int id , dat;
};
bool cmp(node a , node b) {
return a.dat < b.dat;
}
node tmp[N];
void Discretize(int *st , int *ed) {
int n = ed - st;
for(int i = 0 ; i < n ; i++)
tmp[i].id = i , tmp[i].dat = st[i];
sort(tmp , tmp + n , cmp);
int cnt = 1;
st[tmp[0].id] = cnt;
for(int i = 1 ; i < n ; i++) {
if(tmp[i].dat != tmp[i - 1].dat) ++cnt;
st[tmp[i].id] = cnt;
}
}
int a[N];
int n , m , T;
int f[N][N];
int main() {
T = read();
for(int eee = 1 ; eee <= T ; eee++) {
n = read() , m = read();
for(int i = 1 ; i <= n ; i++)
a[i] = read();
Discretize(a + 1 , a + n + 1);
memset(f , 0 , sizeof(f));
for(int i = 1 ; i <= n ; i++) {
f[a[i]][1] += 1;
for(int j = 2 ; j <= m ; j++) {
for(int k = 1 ; k < a[i] ; k++)//这里不是赤裸裸的可以套数据结构吗
f[a[i]][j] += f[k][j - 1];
}
}
int ans = 0;
for(int i = 1 ; i <= n ; i++)
ans += f[i][m];
printf("%d\n" , ans);
}
return 0;
}
3
嵌入树状数组就可以AC啦
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 1010
#define ll long long
#define mod 1000000007ll
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
struct node {
int id , dat;
};
bool cmp(node a , node b) {
return a.dat < b.dat;
}
node tmp[N];
void Discretize(int *st , int *ed) {
int n = ed - st;
for(int i = 0 ; i < n ; i++)
tmp[i].id = i , tmp[i].dat = st[i];
sort(tmp , tmp + n , cmp);
int cnt = 1;
st[tmp[0].id] = cnt;
for(int i = 1 ; i < n ; i++) {
if(tmp[i].dat != tmp[i - 1].dat) ++cnt;
st[tmp[i].id] = cnt;
}
}
int a[N];
int n , m , T;
struct TreeArray {
int siz;
ll a[N * 2];
#define lowbit(_) ((_) & -(_))
void clear() {
siz = n;
memset(a , 0 , sizeof(a));
}
void add(int i , ll dat) {
for( ; i <= siz ; i += lowbit(i))
a[i] = (a[i] + dat) % mod;
}
ll getsum(int r) {
ll sum = 0;
for( ; r ; r -= lowbit(r))
sum = (sum + a[r]) % mod;
return sum;
}
}f[N];
int main() {
T = read();
for(int eee = 1 ; eee <= T ; eee++) {
n = read() , m = read();
for(int i = 1 ; i <= n ; i++)
a[i] = read();
Discretize(a + 1 , a + n + 1);
for(int i = 1 ; i <= m ; i++)
f[i].clear();
for(int i = 1 ; i <= n ; i++) {
f[1].add(a[i] , 1);
for(int j = 2 ; j <= m ; j++) {
f[j].add(a[i] , f[j - 1].getsum(a[i] - 1));
}
}
int ans = 0;
printf("Case #%d: %d\n" , eee , f[m].getsum(n) % mod);
}
return 0;
}
D. 【例题4】区间修改区间查询
题目

思路
设\(b\)为\(a\)的查分数组,则有:
\[\sum^x_{i=1}a_i=\sum^x_{i=1}\sum^i_{j=1}b_i=
\begin{cases}
b_1+\\
b_1+b_2+\\
b_1+b_2+b_3+\\
\cdots\\
b_1+b_2+\cdots+b_x
\end{cases}
=\sum^x_{i=1}(x-i+1)\cdot b_i=\sum^x_{i=1}\big( (x+1)b_i-i\cdot b_i \big)=(x+1)\cdot \sum^x_{i=1}b_i-\sum^x_{i=1}i\cdot b_i
\]
用两个树状数组,一个维护\(b_i\),另一个维护\(i\cdot b_i\)即可
\(i\in [l,r],a_i+=d\),即:\(b_l=b_l+d\qquad b_{r+1}=b_{r+1}-d \qquad ib_l=ib_l+l\cdot d\qquad ib_{r+1}=ib_{r+1}-(r+1)\cdot d\)
查询操作见上
代码
#include <iostream>
#include <cstdio>
using namespace std;
#define N 1000010
#define ll long long
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
struct node {
int siz;
ll a[N * 2];
#define lowbit(_) ((_) & -(_))
void change(int i , ll dat) {
for( ; i <= siz ; i += lowbit(i))
a[i] += dat;
}
ll ask(int r) {
ll sum = 0;
for( ; r ; r -= lowbit(r))
sum += a[r];
return sum;
}
}ib , b;
int n , q;
int a[N];
void change(int l , int r , ll d) {
b.change(l , d);
b.change(r + 1 , -d);
ib.change(l , d * l);
ib.change(r + 1 , -d * (r + 1ll));
}
ll ask(int x) {
return (x + 1ll) * b.ask(x) - ib.ask(x);
}
signed main() {
n = read(); q = read();
b.siz = ib.siz = n;
for(int i = 1 ; i <= n ; i++) {
a[i] = read();
b.change(i , a[i] - a[i - 1]);
ib.change(i , 1ll * i * (a[i] - a[i - 1]));
}
for(int i = 1 ; i <= q ; i++) {
int ty = read() , l = read() , r = read();
if(ty == 1)
change(l , r , read());
else
printf("%lld\n" , ask(r) - ask(l - 1));
}
return 0;
}
E. 【例题5】单点修改区间查询
题目

思路
二维树状数组(见代码),没什么好说的
代码
#include <iostream>
#include <cstdio>
using namespace std;
#define N 5020
#define ll long long
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
int n , m;
struct TreeArray {
ll a[N][N];
#define lowbit(_) ((_) & -(_))
void change(int x , int y , ll d) {
for(int i = x ; i <= n ; i += lowbit(i))
for(int j = y ; j <= m ; j += lowbit(j))
a[i][j] += d;
}
ll ask(int x , int y) {
ll sum = 0;
for(int i = x ; i; i -= lowbit(i))
for(int j = y ; j ; j -= lowbit(j))
sum += a[i][j];
return sum;
}
}a;
int main() {
n = read() , m = read();
while(true) {
int ty;
if(scanf("%d" , &ty) == EOF) return 0;
int lx = read() , ly = read();
if(ty == 1) {
ll d = read();
a.change(lx , ly , d);
}
else {
int rx = read() , ry = read();
printf("%lld\n" , a.ask(rx , ry) - a.ask(lx - 1 , ry) - a.ask(rx , ly - 1) + a.ask(lx - 1 , ly - 1));
}
}
return 0;
}
F. 【例题6】区间修改区间查询
题目

思路
错解
二维线段树:一个节点表示一块矩阵的面积(也可以是点),该矩阵又划分为四个子矩阵(左上,右上,左下,右下),作为它的子节点,然后按普通线段树做
其实这样做的复杂度是不行的(应该是\(O(\max(n,m)\cdot \log (nm)\cdot q)\)),同样,这样的线段树扩展到\(k\)维,单次线段树操作的复杂度是\(O(n^{k-1}\cdot \log n)\),具体原因要从线段树时间复杂度原理考虑,这里不做赘述.
这样做的正确性是没问题的,就是超时了.
算是吸取教训吧
#include <iostream>
#include <cstdio>
#define ll long long
//#pragma GCC optimize(2)
using namespace std;
int n , m;
int read() {
int re = 0;
char c = getchar();
bool sig = false;
while(c < '0' || c > '9') {
if(c == '-') sig = true;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sig ? -re : re;
}
#define N 2048 * 2048 * 4
struct node {
ll tag[N];
ll dat[N];
int Lx[N] , Rx[N] , Ly[N] , Ry[N];
int s1[N] , s2[N] , s3[N] , s4[N];
int root;
#define size(_) ((Rx[_] - Lx[_] + 1) * (Ry[_] - Ly[_] + 1))
void spread(int p) {
tag[s1[p]] += tag[p] , dat[s1[p]] += tag[p] * size(s1[p]);
tag[s2[p]] += tag[p] , dat[s2[p]] += tag[p] * size(s2[p]);
tag[s3[p]] += tag[p] , dat[s3[p]] += tag[p] * size(s3[p]);
tag[s4[p]] += tag[p] , dat[s4[p]] += tag[p] * size(s4[p]);
tag[p] = 0;
dat[0] = tag[0] = 0;
}
int build(int lx , int rx , int ly , int ry) {
static int cnt = 0;
int p = ++cnt;
if(lx > rx || ly > ry) return 0;
Lx[p] = lx , Rx[p] = rx , Ly[p] = ly , Ry[p] = ry;
int mx = (lx + rx) / 2 , my = (ly + ry) / 2;
if(!(lx == rx && ly == ry)) {
s1[p] = build(lx , mx , ly , my);
if(lx != rx) s2[p] = build(mx + 1 , rx , ly , my);
if(ly != ry) s3[p] = build(lx , mx , my + 1 , ry);
if(lx != rx && ly != ry) s4[p] = build(mx + 1 , rx , my + 1 , ry);
}
return p;
}
void change(int lx , int rx , int ly , int ry , ll d , int p) {
if(p == 0) return;
if(lx <= Lx[p] && rx >= Rx[p] && ly <= Ly[p] && ry >= Ry[p]) {
tag[p] += d , dat[p] += size(p) * d;
return;
}
if(lx > Rx[p] || rx < Lx[p] || ly > Ry[p] || ry < Ly[p])
return ;
spread(p);
change(lx , rx , ly , ry , d , s1[p]);
change(lx , rx , ly , ry , d , s2[p]);
change(lx , rx , ly , ry , d , s3[p]);
change(lx , rx , ly , ry , d , s4[p]);
dat[p] = dat[s1[p]] + dat[s2[p]] + dat[s3[p]] + dat[s4[p]];
}
ll ask(int lx , int rx , int ly , int ry , int p) {
if(p == 0) return 0;
if(lx <= Lx[p] && rx >= Rx[p] && ly <= Ly[p] && ry >= Ry[p])
return dat[p];
if(lx > Rx[p] || rx < Lx[p] || ly > Ry[p] || ry < Ly[p])
return 0;
spread(p);
return
ask(lx , rx , ly , ry , s1[p]) +
ask(lx , rx , ly , ry , s2[p]) +
ask(lx , rx , ly , ry , s3[p]) +
ask(lx , rx , ly , ry , s4[p]);
}
}SegTree;
int main() {
n = read() , m = read();
SegTree.root = SegTree.build(1 , n , 1 , m);
while(true) {
int ty;
if(scanf("%d" , &ty) == EOF) return 0;
int lx = read() , ly = read() , rx = read() , ry = read();
if(ty == 1) {
SegTree.change(lx , rx , ly , ry , read() , SegTree.root);
}
else
printf("%lld\n" , SegTree.ask(lx , rx , ly , ry , SegTree.root));
}
return 0;
}
正解(未写)
前两题的结合版,区间查改的二维树状数组



 浙公网安备 33010602011771号
浙公网安备 33010602011771号