「字符串算法」第4章 字典树课堂过关
「字符串算法」第4章 字典树课堂过关
YbtOJ又双叒叕炸掉了
前几分钟还好好的

由于YbtOJ已经炸裂,暂时无法测评,现采用与网络标程对拍的方式验证程序的正确性.
数据生成程序代码放在文章末尾
关于字典树
以前写的:
模板题
由于找不到最直接的模板,就拿了一个最裸的题权当模板
大体思路
应用&结构:用于实现字符串快速检索的多叉树结构
总思路其他博客已经很详尽,这里不再赘述
(其实懒得画图)定义&初始化
定义
trie[SIZE][30](假设只有小写字母),trie[i][j]表示当前在i结点,编号为j的子结点所处的位置,(我们称字符'a'的编号为0,'b'为1,以此类推),即trie是一个用于模拟指针的数组,定义一个特殊的空结点(一般为0),所有的指针均指向空定义
end[SIZE],end[i]表示下标为i的结点是否为某个字符串的终点插入
void insert(char *s , int siz) { static int top = 1;//trie的第一维最大下标,类似于链式前向星 int p = 1; for(int i = 1 ; i <= siz ; i++) { int c = s[i] - 'a'; if(trie[p][c] == 0)//如果指向空,则新建结点 trie[p][c] = ++top; p = trie[p][c]; } vis[p] = false; end[p] = true; }查找(以模板为例)
int search(char *s , int siz) { int p = 1; for(int i = 1 ; i <= siz ; i++) { p = trie[p][s[i] - 'a']; if(p == 0) return 0;//当前字符串在trie树中不存在 } if(end[p] == false) return 0;//WRONG if(vis[p] == true) return 2;//REPEAT vis[p] = true;//标记当前字符串已经访问过 return 1;//OK }模板题完整代码
#include <iostream> #include <cstdio> #define nn 500010 using namespace std; int sread(char *s) { int siz = 1; do s[siz] = getchar(); while(s[siz] < 'a' || s[siz] > 'z'); while(s[siz] >= 'a' && s[siz] <= 'z') s[++siz] = getchar(); --siz; return siz; } bool vis[nn] , end[nn]; int trie[nn][30]; void insert(char *s , int siz) { static int top = 1; int p = 1; for(int i = 1 ; i <= siz ; i++) { int c = s[i] - 'a'; if(trie[p][c] == 0) trie[p][c] = ++top; p = trie[p][c]; } vis[p] = false; end[p] = true; } int search(char *s , int siz) { int p = 1; for(int i = 1 ; i <= siz ; i++) { p = trie[p][s[i] - 'a']; if(p == 0) return 0; } if(end[p] == false) return 0;//WRONG if(vis[p] == true) return 2;//REPEAT vis[p] = true; return 1;//OK } int n , m; char s[nn]; int main() { cin >> n; for(int i = 1 ; i <= n ; i++) { int siz = sread(s); insert(s , siz); } cin >> m; for(int i = 1 ; i <= m ; i++) { int siz = sread(s); int res = search(s , siz); if(res == 0) puts("WRONG"); else if(res == 1) puts("OK"); else puts("REPEAT"); } return 0; }
A. 【例题1】前缀统计
题目
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 1000010
#define TrieRoot 1
using namespace std;
int trie[nn][30];
int end[nn];
void insert(char *s) {
static int cnt = 2;
int p = TrieRoot , len = strlen(s);
for(int i = 0 ; i < len ; i++) {
if(trie[p][s[i] - 'a'] == 0)
trie[p][s[i] - 'a'] = cnt++;
p = trie[p][s[i] - 'a'];
}
++end[p];
}
int solve(char *s) {
int len = strlen(s);
int p = TrieRoot;
int ans = 0;
for(int i = 0 ; i < len ; i++) {
ans += end[p];
p = trie[p][s[i] - 'a'];
}
ans += end[p];
return ans;
}
int n , m;
char s[nn];
int main() {
scanf("%d %d" , &n , &m);
for(int i = 1 ; i <= n ; i++) {
scanf("%s" , s);
insert(s);
}
for(int i = 1 ; i <= m ; i++) {
scanf("%s" , s);
printf("%d\n" , solve(s));
}
return 0;
}
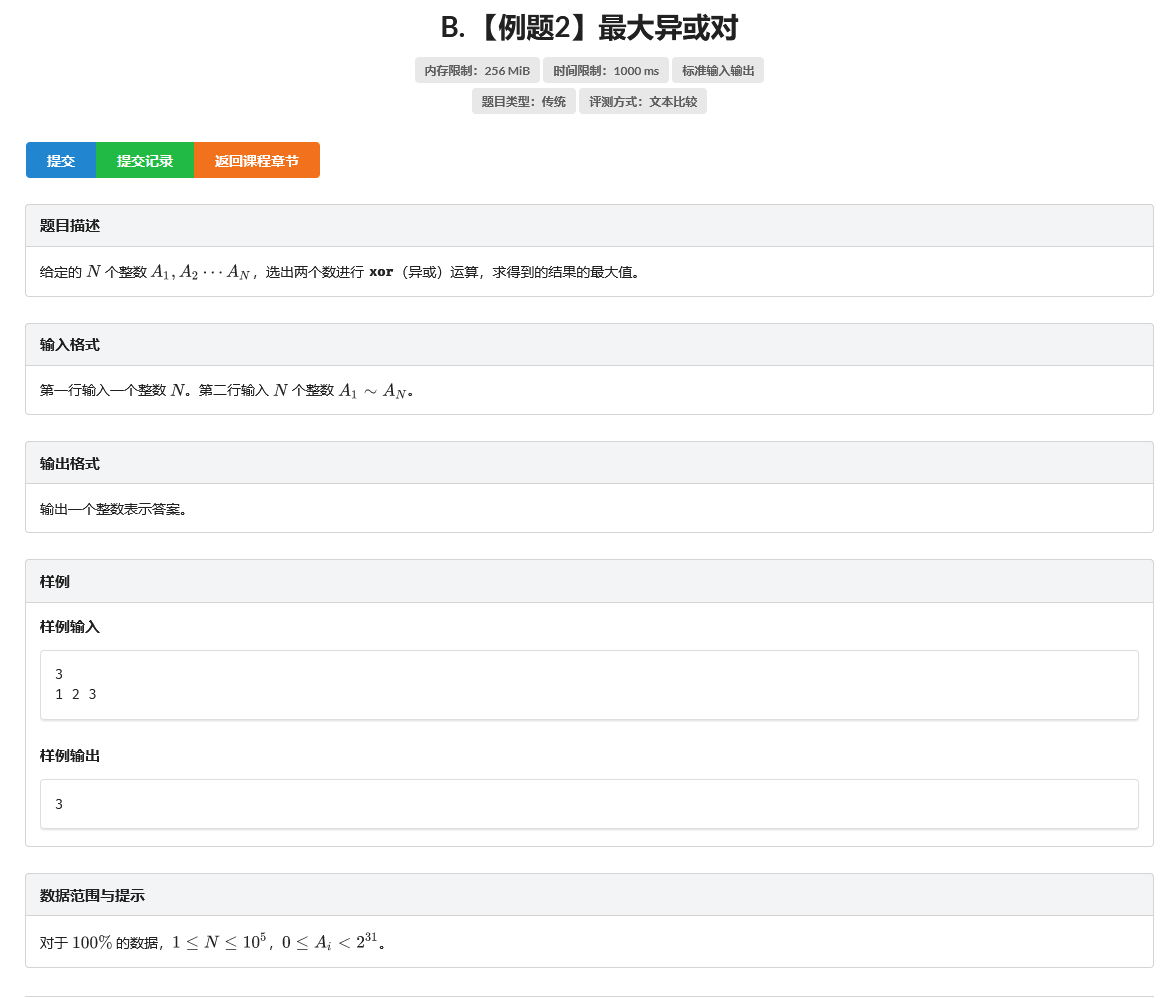
B. 【例题2】最大异或对
题目
代码
#include <iostream>
#include <cstdio>
#define int unsigned
#define nn 100010 * 30
#define TrieRoot 1
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int trie[nn][2];
int rev(int x) {
int res = 0;
for(int i = 1 ; i <= 31 ; i++) {
res = (res << 1) + (x & 1);
x >>= 1;
}
return res;
}
void insert(int x) {
static int cnt = TrieRoot + 1;
int p = TrieRoot;
for(int i = 1 ; i <= 31 ; i++) {
int tmp = (x & 1);
if(trie[p][tmp] == 0)
trie[p][tmp] = cnt++;
p = trie[p][tmp];
x >>= 1;
}
}
int n;
int a[100010];
signed main() {
n = read();
for(int i = 1 ; i <= n ; i++) {
a[i] = rev(read());
insert(a[i]);
}
int ans = 0;
for(int i = 1 ; i <= n ; i++) {
int res = 0;
int tmp = a[i];
int p = TrieRoot;
for(int j = 1 ; j <= 31 ; j++) {
if(trie[p][(tmp & 1) ^ 1] != 0)
p = trie[p][(tmp & 1) ^ 1] , res = (res << 1) + 1;
else
p = trie[p][tmp & 1] , res = (res << 1);
tmp >>= 1;
}
if(res > ans)
ans = res;
}
cout << ans;
return 0;
}
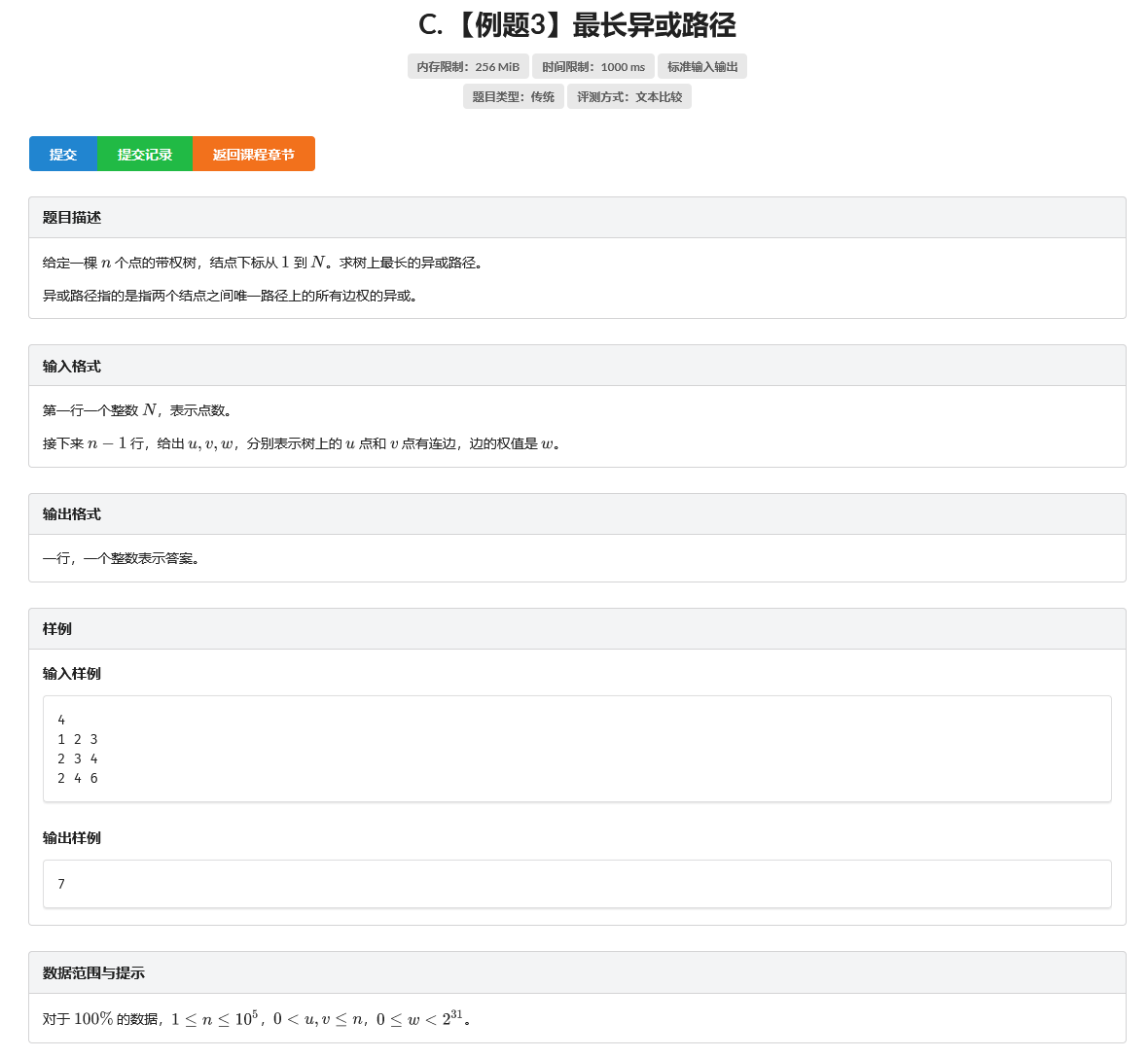
C. 【例题3】最长异或路径
题目
思路 & 代码
题目
思路
别在意这是一道紫题,其实还是能做的首先要知道:异或运算满足交换律,结合律,\(a\ xor\ a = 0\),一个点A到另一个点B的异或路径长度等于(A到C的异或路径长度 xor B到C的异或路径长度),其中C为任一点
为什么?
假设C是树的根,后者只是比前者多跑了2遍C到lca(A,B)的路径,也就是这条路径上的边会被异或两边,又因为同一个数异或的结果为0,所以这多跑的2遍对结果无影响
所以,我们随便选一个点作为根(这里就用1号点),求出所有点到1号点的异或路径长度,存在
dis[]中,这样,我们就能\(O(1)\)求出两个点之间的异或路径长度到此,原问题转化为:
找一对
i,j,使dis[i] ^ dis[j]最大(" ^ "表示异或)01trie是解决这种异或问题的利器,但是,怎么找呢?
先说01trie:按照
dis[i]从二进制下高位到低位,从根到叶子的顺序建树(懒得画图了,自己看代码理解下)然后?
我在没看题解时的思路:
- 从trie的根结点开始向下找,直到遇到分支(因为此时高位是1,高位大的一定大)
- 找到分支后,用BFS+贪心查找最优解(尽量让两个数异或后高位为1)
- 但是,最坏情况下,时间复杂度是可以去到\(2^{30}\)的
因此,看了一波题解
正解:
- \(O(n)\)枚举每一个\(dis_i\)
- \(O(30)\)在trie中贪心查找另一个\(trie_j\),使
trie[i] ^ trie[j]最大(这里的贪心其实就是让异或出来的结果高位更大,这也就决定了如何建trie树)反思
其实我的思路离正解已经很近了,可以说只差了最后一步,但是失之毫厘差之千里,复杂的几乎就是\(O(n^2)\)的纯暴力和正解的区别,应该从多方面思考问题的解,优化程序中复杂度最高的地方
代码
#include <iostream> #include <cstdio> #define nn 100010 using namespace std; int read() { int re = 0 , sig = 1; char c = getchar(); while(c < '0' || c > '9') { if(c == '-')sig = -1; c = getchar(); } while(c >= '0' && c <= '9') re = (re << 1) + (re << 3) + c - '0', c = getchar(); return re * sig; } struct ednode{//链式前向星 int nxt , w , to; }ed[nn * 2]; int head[nn]; inline void addedge(int u , int v , int w) { static int top = 1; ed[top].to = v , ed[top].w = w , ed[top].nxt = head[u] , head[u] = top; ++top; } int dis[nn]; int n; int trie[nn * 30][3]; void dfs(int x , int pre) {//处理出dis数组 for(int i = head[x] ; i ; i = ed[i].nxt) { if(ed[i].to == pre)continue; dis[ed[i].to] = dis[x] ^ ed[i].w; dfs(ed[i].to , x); } } void build() {//建trie树 int top = 1; for(int i = 1 ; i <= n ; i++) { int tmp = dis[i]; int p = 1; for(int j = 30 ; j >= 0 ; j--) { int x = (tmp >> j) & 1; if(trie[p][x] == 0) trie[p][x] = ++top; p = trie[p][x]; } } } int GetAns() { int ans = 0; for(int i = 1 ; i <= n ; i++) {//枚举每一个dis int tmp = dis[i]; int res = 0; int p = 1; for(int j = 30 ; j >= 0 ; j--) {//找到最优的另一个dis,满足它和dis[i]的异或值最大 if(trie[p][!((tmp >> j) & 1)] != 0) { res += (1 << j); p = trie[p][!((tmp >> j) & 1)]; } else p = trie[p][(tmp >> j) & 1]; } if(res > ans) ans = res; } return ans; } int main() { n = read(); for(int i = 1 ; i < n ; i++) { int u , v , w; u = read(); v = read(); w = read(); addedge(u , v , w); addedge(v , u , w); } dfs(1 , 0); build(); cout << GetAns(); return 0; } /*洛谷样例2 10 1 2 12188248 2 3 2060207469 1 4 960096258 1 5 681126748 3 6 719580677 6 7 2084644229 4 8 730246277 1 9 668729523 9 10 1055107866 2084644229 */
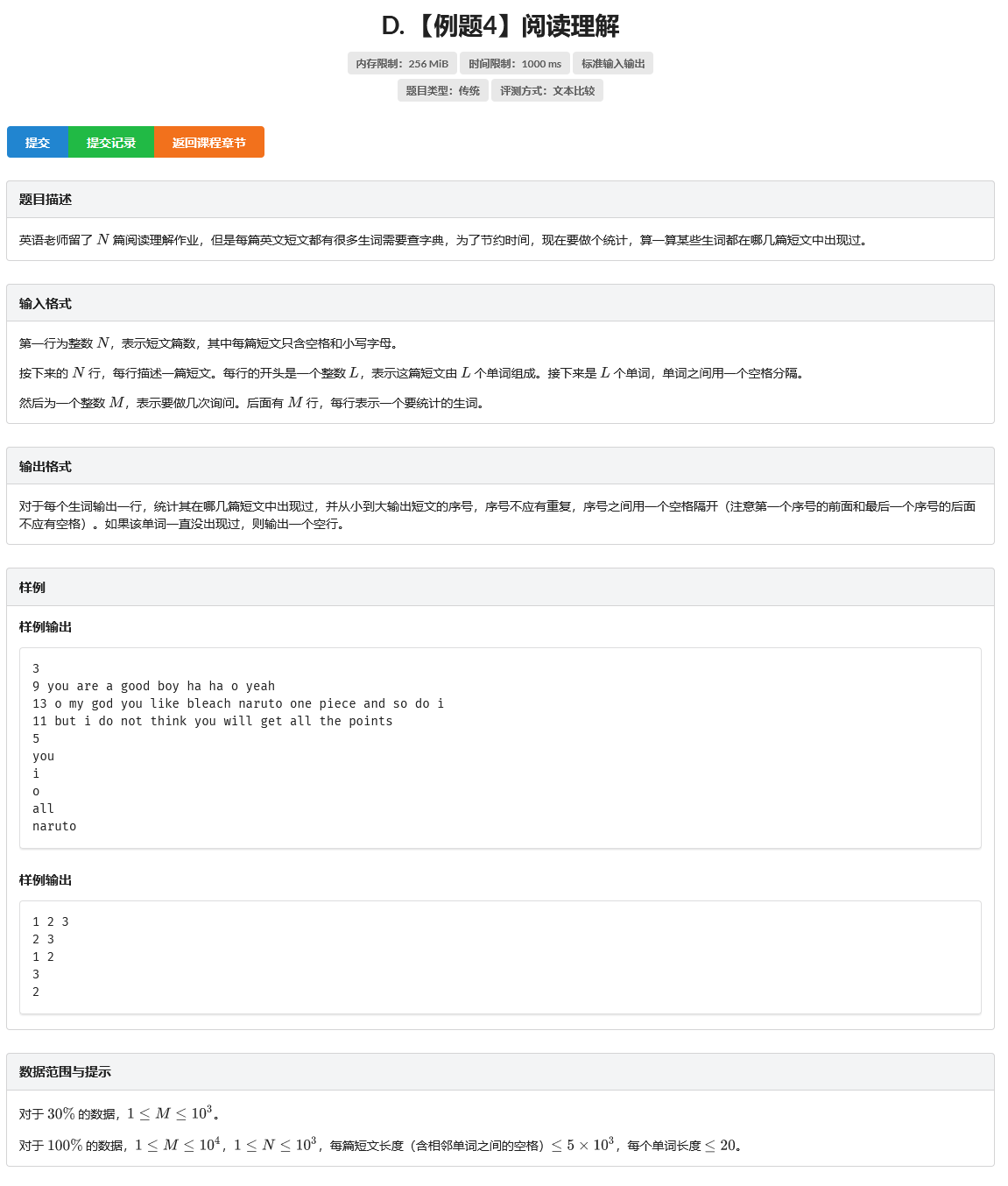
D. 【例题4】阅读理解
题目
思路
很简单的一道题(别看是蓝的)
对于字典树的每一个节点,捆绑一个\(head\)指针,用类似链式前向星的方式存储该单词所在的文章,如代码:
int trie[nn][30];
int head[nn] , nxt[nn] , dat[nn];
inline void insert(char *s , int article) {
static int cnt = TrieRoot + 1;
int len = strlen(s);
int p = TrieRoot;
for(int i = 0 ; i < len ; i++) {
if(trie[p][s[i] - 'a'] == 0)
trie[p][s[i] - 'a'] = cnt++;
p = trie[p][s[i] - 'a'];
}
//单词插入完毕
static int cnt2 = 1;
for(int i = head[p] ; i ; i = nxt[i])//检查是否重复,其实不用循环好像也可以(个人没有验证)
if(dat[i] == article)
return;
dat[cnt2] = article , nxt[cnt2] = head[p] , head[p] = cnt2;//将当前article插入到链中
++cnt2;
}
由于我们遍历文章的顺序是从1到\(n\),所以链中的文章一定是倒序的,用递归输出即可(详见完整代码)
代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 1000010
#define TrieRoot 1
using namespace std;
int trie[nn][30];
int head[nn] , nxt[nn] , dat[nn];
inline void insert(char *s , int article) {
static int cnt = TrieRoot + 1;
int len = strlen(s);
int p = TrieRoot;
for(int i = 0 ; i < len ; i++) {
if(trie[p][s[i] - 'a'] == 0)
trie[p][s[i] - 'a'] = cnt++;
p = trie[p][s[i] - 'a'];
}
static int cnt2 = 1;
for(int i = head[p] ; i ; i = nxt[i])
if(dat[i] == article)
return;
dat[cnt2] = article , nxt[cnt2] = head[p] , head[p] = cnt2;
++cnt2;
}
inline void print(int p) {
if(p == 0) return;
print(nxt[p]);
printf("%d " , dat[p]);
}
inline void solve(char *s) {
int p = TrieRoot;
int len = strlen(s);
for(int i = 0 ; i < len ; i++)
p = trie[p][s[i] - 'a'];
print(head[p]);
}
int n , m;
char s[110];
int main() {
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++) {
int L;
scanf("%d" , &L);
for(int j = 1 ; j <= L ; j++) {
scanf("%s" , s);
insert(s , i);
}
}
scanf("%d" , &m);
for(int i = 1 ; i <= m ; i++) {
scanf("%s" , s);
solve(s);
putchar('\n');
}
return 0;
}
随机数据生成
A. 【例题1】前缀统计
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (long long)rand() * rand() * rand() % (r - l + 1) + l;
}
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int n = random(1000) , m = random(1000);
printf("%d %d\n" , n , m);
for(int i = 1 ; i <= n ; i++) {
int len = random(10);
while(len--)
putchar(random('z' , 'a'));
putchar('\n');
}
for(int i = 1 ; i <= m ; i++) {
int len = random(1e6 / n);
while(len--)
putchar(random('z' , 'a'));
putchar('\n');
}
return 0;
}
B. 【例题2】最大异或对
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (long long)rand() * rand() * rand() % (r - l + 1) + l;
}
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int n = random(1e5);
cout << n << '\n';
for(int i = 1 ; i <= n ; i++) {
printf("%d " , random((1u << 31) - 1) );
}
return 0;
}
D. 【例题4】阅读理解
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (long long)rand() * rand() * rand() % (r - l + 1) + l;
}
char s[100010][30];
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int wordnum = 1e5;
for(int i = 1 ; i <= wordnum ; i++) {
int len = random(20);
for(int j = 0 ; j < len ; j++)
s[i][j] = random('z' , 'a');
}
int n = random(1e3) , m = random( min(wordnum , (int)1e4));
printf("%d\n" , n);
for(int i = 1 ; i <= n ; i++) {
int len = random(100);
printf("%d " , len);
for(int j =1 ; j <= len ; j++) {
printf("%s " , s[random(wordnum)]);
}
}
printf("%d\n" , m);
for(int i = 1 ; i <= m ; i++) {
puts(s[i]);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号