「字符串算法」第2章 Hash 和 Hash 表课堂过关
「字符串算法」第2章 Hash 和 Hash 表课堂过关
先贴上:对拍程序
Hash
- 把任意字符串映射成唯一一个非负整数的算法
- 产生冲突概率极小
- 通过hash值可以实现快速查找与匹配
- 常用
unsigned long long自然溢出取代模运算 - 多次哈希:采用不同\(p\),\(mod\)多算几次,只有当值全部相等是才认为两个字符串相等(\(p\)是进制数,\(mod\)是模数)
- \(p\)常取\(131,13331\),此时产生冲突概率较低
Hash模板
ul Hash(char *s) {
//将单个字符(包含大小写字符,数字)映射为数字value,value∈[0,p]
#define value(_) (ul)((_ >= '0' && _ <= '9' ? (_ - '0' + 26) : (_ >= 'a' && _ <= 'z' ? _ - 'a' : _ - 'A' + 26) ))
int siz = strlen(s);
ul key = 0;
for(int i = 0 ; i <= siz ; i++) {
key = key * 131ull + (ul)i * value(s[i]);//131ull即p,乘p相当于key在p进制下左移一位
}
return key;
}
Hash模板2-子串哈希值+双重哈希
以【例题2】回文子串 为例
//p,mod的取值
const int p = 131 , p2 = 97;
const ul mod = 1000000007 , mod2 = 19260817;
预处理
ha[0] = s[0] - 'a';
rha[0] = res[0] - 'a';
ha2[0] = s[0] - 'a';
rha2[0] = res[0] - 'a';
for(rr int i = 1 ; i < siz ; i++)
ha[i] = (ha[i - 1]* p + s[i] - 'a') % mod,
rha[i] = (rha[i - 1] * p + res[i] - 'a') % mod,//res是s的反转串,rha和rha2是res的两个预处理数组
ha2[i] = (ha2[i - 1]* p2 + s[i] - 'a') % mod2,
rha2[i] = (rha2[i - 1] * p2 + res[i] - 'a') % mod2;
获取子串哈希值
void check(int L , int R) {
int L = i - mid + 1 , R = i + mid - 1;
ul key1 , key2;
//pw[i]是p的i次方,pw2[i]是p2的i次方
// 为了防止出现负数,这里先加上mod "pw[R - L + 1] * "相当于p进制下左移R-L+1为(可以参考二进制的位运算)
key1 = (ha[R] + mod - pw[R - L + 1] * ((L == 0) ? 0 : ha[L - 1]) % mod) % mod,
//反转后 L对应siz-L-1 R对应siz-R-1
key2 = (rha[siz - L - 1] + mod - pw[R - L + 1] * ((siz - R - 2 < 0) ? 0 : rha[siz - R - 1 - 1]) % mod) % mod;
if(key1 != key2)//哈希值匹配
res = false;
else {//对拍时出现了较高的错误率,因此采用了二次哈希
key1 = (ha2[R] + mod2 - pw2[R - L + 1] * ((L == 0) ? 0 : ha2[L - 1]) % mod2) % mod2,
key2 = (rha2[siz - L - 1] + mod2 - pw2[R - L + 1] * ((siz - R - 2 < 0) ? 0 : rha2[siz - R - 1 - 1]) % mod2) % mod2;
res = (key1 == key2);
}
return res;
}
若不能理解,自己从\(p\)进制角度推一下即可
Hash模板3-二维Hash
摘自信息学奥赛一本通-高效进阶
一维Hash是把一个字符串或一个序列用一个整数表示,二维Hash是把一个矩阵用一个整数表示.
我们进行两次Hash,第一次,我们横着Hash:
for(int i = 1 ; i <= n ; i++) for(int j = 1 ; j <= m ; j++) hash[i][j] = hash[i][j - 1] * p1 + a[i][j]此时\(hash(i,j)\)表示第\(i\)行前\(j\)个数的Hash值,此时我们进行第二次Hash:
for(int i = 1 ; i <= n ; i++) for(int j = 1 ; j <= m ; j++) hash[i][j] += hash[i - 1][j] * p2;若我们要查询左上角为\((x,y)\) 右下角为\((x_1,y_1)\)的矩阵的Hash值就为:
\[hash(x_1,y_1)-hash(x-1,y_1)\cdot p_2^{x_1-x+1}-hash(x_1,y-1)\cdot p_1^{y_1-y+1}+hash(x-1,y-1)\cdot p_1^{y_1-y+1}\cdot p_2^{x_1-x+1} \]写成代码:
key = hs[x1][y1] + hs[x - 1][y - 1] * pw1[y1 - y + 1] * pw2[x1 - x + 1] - hs[x - 1][y1] * pw2[x1 - x + 1] - hs[x1][y - 1] * pw1[y1 - y + 1]
关于Hash自然溢出做减法运算的一个问题
做取模运算时,为了避免负数,常常会用以下语句:c=(mod+a-b)%mod,但是自然溢出的情况下,模数为\(2^{64}\),已经超出unsigned long long的范围,用上述方法自然会有问题.
其实在自然溢出的情况下,我们不用加上模数,也就是说若\(a<b\),则\(a-b==(1ull<<64)-b+a\)成立(\(a,b\)均为unsigned long long类型),可以自己验证一下,具体原因跟运算方式有关,本人比较菜,说不清楚
这是我做到T3才意识到的,不然T2我也不会傻傻敲双哈希
关于回文串处理的一个问题
为了避免对奇偶性的讨论,在处理回文串问题时,我们常常把字符串"abcb"变成"?a?b?c?b?", '?'代表一种特殊字符,但是这个字符的ASCLL码需要尽量高一些,或者直接为它赋一个独特的\(value\),不然在Hash的时候出现负数的\(value\)会造成冲突概率大大上升
A. 【例题1】字符串哈希
题目
代码
AC代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ul unsigned long long
using namespace std;
ul Hash(char *s) {
#define value(_) (ul)((_ >= '0' && _ <= '9' ? (_ - '0' + 26) : (_ >= 'a' && _ <= 'z' ? _ - 'a' : _ - 'A' + 26) ))
int siz = strlen(s);
ul key = 0;
for(int i = 0 ; i <= siz ; i++) {
key = key * 63ull + (ul)i * value(s[i]);
}
return key;
}
int n;
char c[10010][1510];
ul key[10010];
int main() {
int T;
cin >> T;
while(T--) {
memset(c , 0 , sizeof(c));
memset(key , 0 , sizeof(key));
scanf("%d" , &n);
for(int i = 1 ; i <= n ; i++)
scanf("%s" , &c[i]);
for(int i = 1 ; i <= n ; i++) {
key[i] = Hash(c[i]);
}
sort(key + 1 , key + n + 1);
int cnt = 1;
for(int i = 2 ; i <= n ; i++) {
if(key[i] != key[i - 1])
cnt++;
}
cout << cnt << endl;
}
return 0;
}
随机数据生成
可以自己测一下Hash的错误率
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (unsigned long long) rand() * rand() * rand() % (r - l + 1) + l;
}
string st = "0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUIOPASDFGHJKLZXCVBNM";
string dict[1010];
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int T = 2;
cout << T << endl;
while(T--) {
int n = 1000;
for(int i = 1 ; i <= n ; i++) {
int siz = 1000 + random(500 , -750);
for(int j = 1 ; j <= siz ; j++)
dict[i] += st[random(st.size() - 1 , 0)];
}
cout << n << endl;
for(int i = 1 ; i <= n ; i++) {
cout << dict[random(n)] << endl;
}
}
return 0;
}
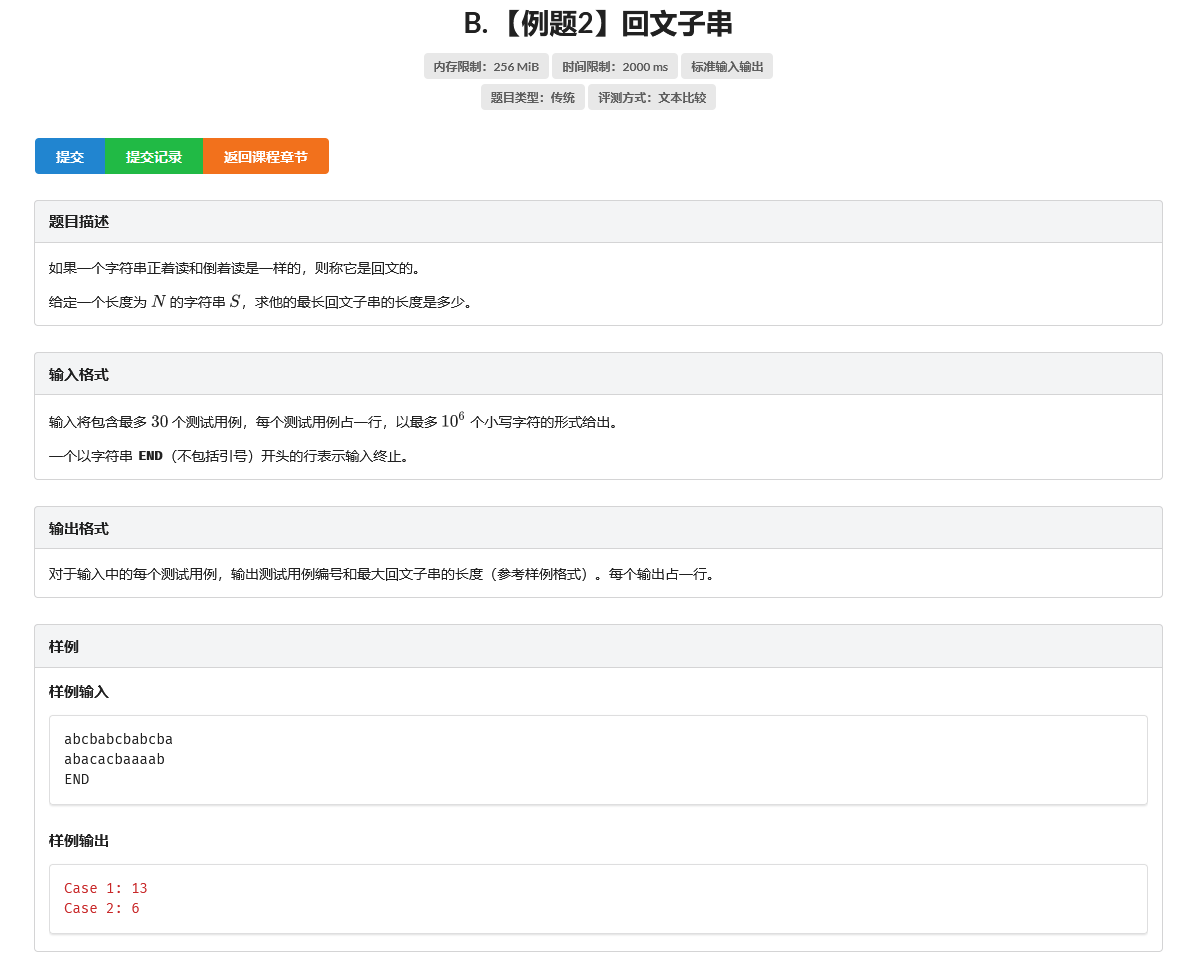
B. 【例题2】回文子串
题目
说明:自己出的数据,强度较大,仅供参考(数据强度:\(5\cdot 30\cdot 10^6\),5组数据,每组30个字符串,每个字符串最大长度为\(10^6\))
小技巧
对于字符串"abacacbaaaab",我们可以将它变为"{a{b{a{c{a{c{b{a{a{a{a{b{"最后在对答案进行处理,以避免回文串长度奇偶性问题
代码
AC代码
**说明:一下代码本地跑很慢,但是不知道Ybt上为什么能AC,估计是自带O2 **
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 2000010
#define ul unsigned long long
#define rr register
//#pragma GCC optimize(2)
using namespace std;
char s[nn];
char tmp[nn];
char res[nn];
int siz;
const int p = 131 , p2 = 97;
const ul mod = 1000000007 , mod2 = 19260817;
ul pw[nn];
ul pw2[nn];
ul ha[nn];
ul rha[nn];
ul ha2[nn];
ul rha2[nn];
int work() {
memset(s , 0 , sizeof(s));
memset(ha , 0 , sizeof(ha));
memset(rha , 0 , sizeof(rha));
siz = 0;
char c_ = getchar();
while(c_ < 'a' || c_ > 'z') {
if(c_ == 'E') return -1;
c_ = getchar();
}
while(c_ >= 'a' && c_ <= 'z') {
tmp[siz++] = c_;
c_ = getchar();
}
// siz = strlen(tmp);
s[0] = '{';
for(rr int i = 0 ; i < siz ; ++i)
s[(i << 1) + 1] = tmp[i] , s[(i << 1) + 2] = '{';
siz = siz * 2 + 1;
for(rr int i = 0 ; i < siz ; ++i)
res[i] = s[siz - i - 1];
//===为了减小常数,把上面函数里的东西全部放到这里了
ha[0] = s[0] - 'a';
rha[0] = res[0] - 'a';
ha2[0] = s[0] - 'a';
rha2[0] = res[0] - 'a';
for(rr int i = 1 ; i < siz ; i++)
ha[i] = (ha[i - 1]* p + s[i] - 'a') % mod,
rha[i] = (rha[i - 1] * p + res[i] - 'a') % mod,
ha2[i] = (ha2[i - 1]* p2 + s[i] - 'a') % mod2,
rha2[i] = (rha2[i - 1] * p2 + res[i] - 'a') % mod2;
//===
int max_ = 1;
for(rr int i = 0 ; i < siz ; ++i) {
rr bool sig = false;
rr int l = 1 , r = i + 1;
if(r > siz - i) r = siz - i;
int mid;
while(l < r) {
mid = (l + r) >> 1;
if(((l + r) & 1) != 0) ++mid;
bool res;
//===匹配
int L = i - mid + 1 , R = i + mid - 1;
ul key1 , key2;
key1 = (ha[R] + mod - pw[R - L + 1] * ((L == 0) ? 0 : ha[L - 1]) % mod) % mod,
key2 = (rha[siz - L - 1] + mod - pw[R - L + 1] * ((siz - R - 2 < 0) ? 0 : rha[siz - R - 1 - 1]) % mod) % mod;
if(key1 != key2)
res = false;
else {
key1 = (ha2[R] + mod2 - pw2[R - L + 1] * ((L == 0) ? 0 : ha2[L - 1]) % mod2) % mod2,
key2 = (rha2[siz - L - 1] + mod2 - pw2[R - L + 1] * ((siz - R - 2 < 0) ? 0 : rha2[siz - R - 1 - 1]) % mod2) % mod2;
res = (key1 == key2);
}
//===
if(res)
l = mid;
else
r = mid - 1;
if(r <= max_) {sig = true ; break;}
}
if(sig) continue;
int tmp = l - 1;
if(max_ < tmp)
max_ = tmp;
}
return max_;
//*/
}
int main() {
pw[0] = 1;
for(int i = 1 ; i <= 1000010 ; i++)
pw[i] = pw[i - 1] * p % mod;
pw2[0] = 1;
for(int i = 1 ; i <= 1000010 ; i++)
pw2[i] = pw2[i - 1] * p2 % mod2;
int ans , cnt = 0;
while((ans = work()) != -1)
printf("Case %d: %d\n" , ++cnt , ans);
return 0;
}
随机数据生成
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (long long) rand() * rand() * rand() % (r - l + 1) + l;
}
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
for(int i = 1 ; i <= 30 ; i++) {
int siz = random(1e6);
for(int j = 1 ; j <= siz ; j++)
putchar(random('z' , 'a'));
putchar('\n');
}
puts("END");
return 0;
}
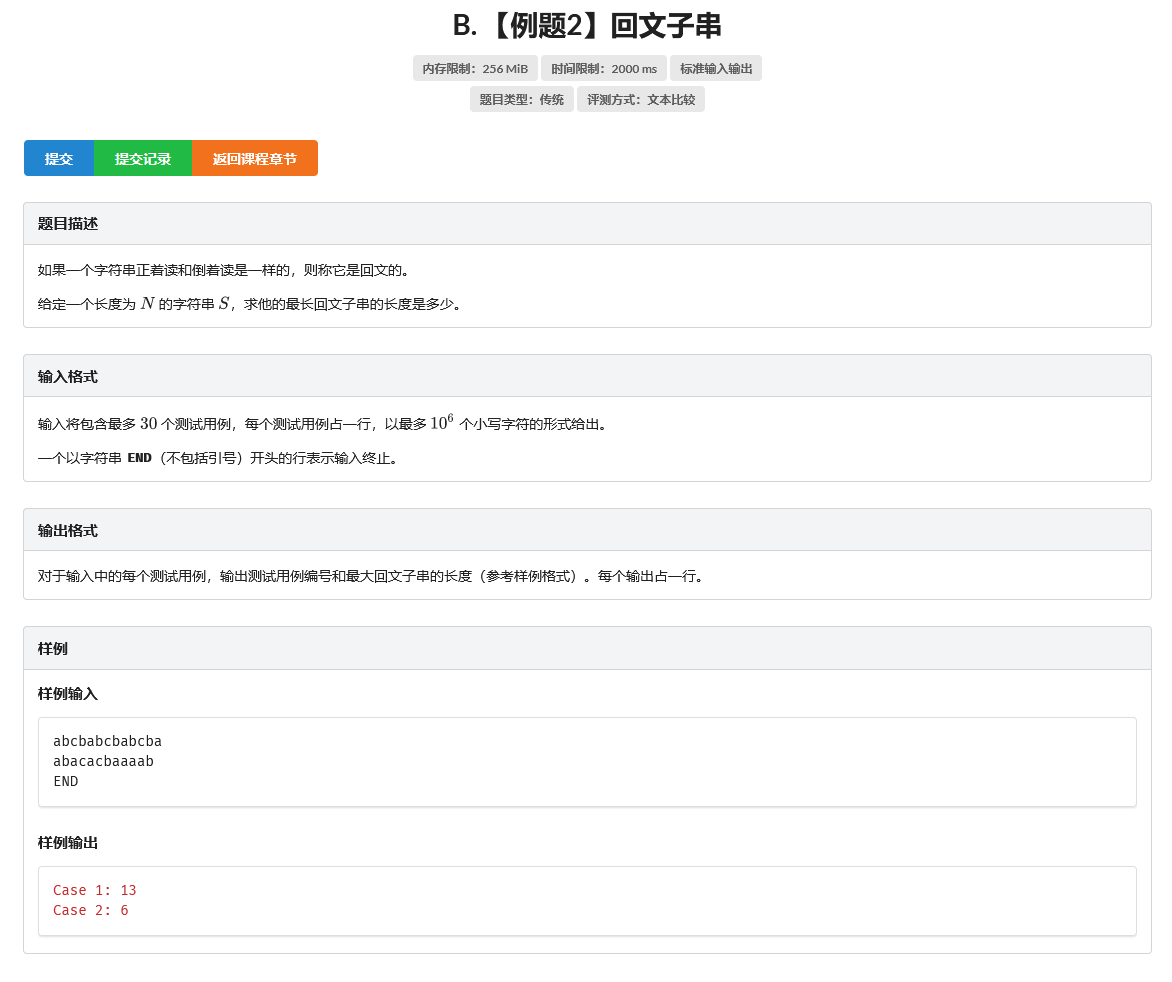
C. 【例题3】对称正方形
题目
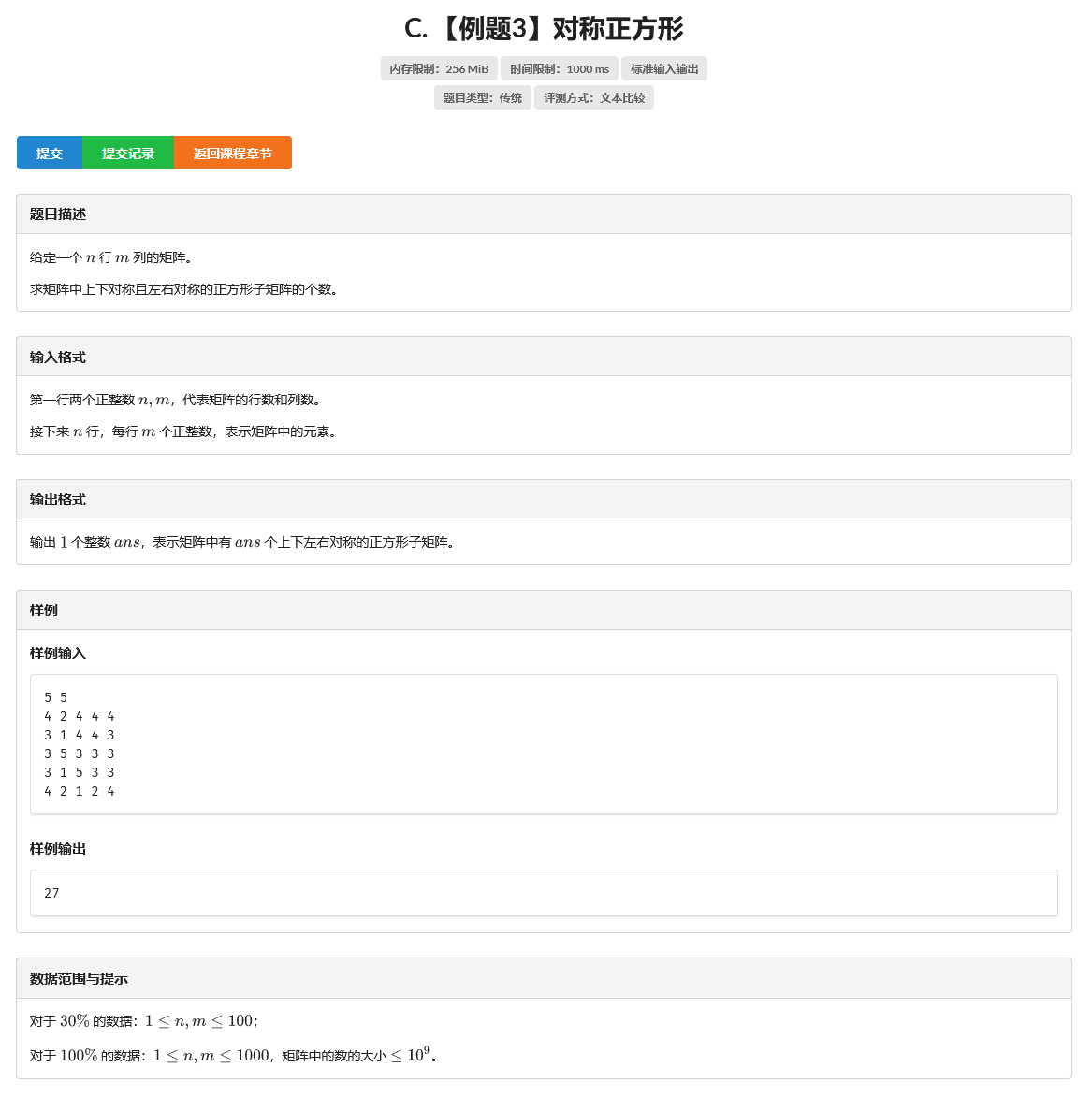
思路
最简单的做法是枚举正方形左上角顶点的横纵坐标,正方形边长,时间复杂度\(O(n^3)\),用Hash进行\(O(1)\)判断对称,期望得分\(30\)
优化一下,如果一个正方形合法,那么把该正方形四周一圈削掉也一样合法,因此,我们考虑枚举一个正方形的中心,二分其最大边长\(l\),使该正方形恰好满足对称\(ans\)直接加上\(l\)即可,时间复杂度\(O(n\cdot m\log n)\),期望得分\(100\)
另外,对于边长为偶数的正方形,其中心不在数上,需要单独在做一个二分处理
一个我一开始忽略的小问题:
做哈希的时候,最少有三个矩阵(一般为原矩阵,水平翻转,竖直反转),我一开始只有两个矩阵(原矩阵,原矩阵水平翻转再后竖直翻转的矩阵),错因是像下面这样的矩阵会被判合法,导致输出答案大于标准答案
1 2
2 1
对于矩阵翻转后坐标变换问题,这里不再赘述,可以自己推一下,或参考下面可读性极低的代码
代码
AC代码
#include <iostream>
#include <cstdio>
#define nn 3010
#define ul unsigned long long
#define rr register
using namespace std;
ul read() {
ul re = 0;
char c = getchar();
while(c < '0' || c > '9')c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
const ul p1 = 1331 , p2 = 13331;
int n , m;
int mat[nn][nn];
int res[nn][nn];
int rres[nn][nn];
ul hs[nn][nn];
ul rhs[nn][nn];
ul rrhs[nn][nn];
ul pw1[nn] , pw2[nn];
inline bool check(int i , int j , int k) {//判断以(i,j)为左上角顶点,边长为k+1的矩阵是否合法
int x = i , y = j , x1 = i + k , y1 = j + k;
ul key1 = hs[x1][y1] + hs[x - 1][y - 1] * pw1[y1 - y + 1] * pw2[x1 - x + 1] - hs[x - 1][y1] * pw2[x1 - x + 1] - hs[x1][y - 1] * pw1[y1 - y + 1];
x = n - x1 + 1 , y = m - y1 + 1 , x1 = n - i + 1 , y1 = m - j + 1;
ul key2 = rhs[x1][y1] + rhs[x - 1][y - 1] * pw1[y1 - y + 1] * pw2[x1 - x + 1] - rhs[x - 1][y1] * pw2[x1 - x + 1] - rhs[x1][y - 1] * pw1[y1 - y + 1];
if(key1 != key2) return false;
int t;
x = i , y = j , x1 = i + k , y1 = j + k;
x = n - x + 1 , x1 = n - x1 + 1;
t = x , x = x1 , x1 = t;
ul key3 = rrhs[x1][y1] + rrhs[x - 1][y - 1] * pw1[y1 - y + 1] * pw2[x1 - x + 1] - rrhs[x - 1][y1] * pw2[x1 - x + 1] - rrhs[x1][y - 1] * pw1[y1 - y + 1];
return key1 == key3;
}
#define min_(_ , __) ((_) < (__) ? (_) : (__))
int main() {
pw1[0] = pw2[0] = 1;
for(int i = 1 ; i <= 3000 ; i++)
pw1[i] = pw1[i - 1] * p1,
pw2[i] = pw2[i - 1] * p2;
n = read();
m = read();
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
mat[i][j] = res[n - i + 1][m - j + 1] = rres[n - i + 1][j] = read();
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
hs[i][j] = hs[i][j - 1] * p1 + mat[i][j],
rhs[i][j] = rhs[i][j - 1] * p1 + res[i][j],
rrhs[i][j] = rrhs[i][j - 1] * p1 + rres[i][j];
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
hs[i][j] += hs[i - 1][j] * p2,
rhs[i][j] += rhs[i - 1][j] * p2,
rrhs[i][j] += rrhs[i - 1][j] * p2;
/*暴力
int ans = 0;
for(rr int i = 1 ; i <= n ; ++i)
for(rr int j = 1 ; j <= m ; ++j) {
for(rr int k = 0 ; k + i <= n && k + j <= m ; ++k) {
if(check(i , j , k)) {
// printf("%d %d %d\n" , i , j , k);
++ans;
}
}
}/*/
int ans = 0;
for(int i = 1 ; i <= n ; i++)//边长为奇数
for(int j = 1 ; j <= m ; j++) {
int l = 1 , r = min_(min_(i , j) , min_(n - i + 1 , m - j + 1));
while(l < r) {
int mid = (l + r) / 2;
if((l + r) % 2 == 1) ++mid;
if(check(i - mid + 1 , j - mid + 1 , mid * 2 - 2))
l = mid;
else
r = mid - 1;
}
ans += l;
}
for(int i = 1 ; i <= n ; i++)//边长为偶数
for(int j = 1 ; j <= m ; j++) {
int l = 0 , r = min_(min_(i , j) , min_(n - i , m - j ));
while(l < r) {
int mid = (l + r) / 2;
if((l + r) % 2 == 1) ++mid;
if(check(i - mid + 1 , j - mid + 1 , mid * 2 - 1))
l = mid;
else
r = mid - 1;
}
ans += l;
}
/*
puts("\n\n");
for(int i = 1 ; i <= n ; i++) {
for(int j = 1 ; j <= m ; j++)
cout << rres[i][j] <<' ';
cout << endl;
}*/
cout << ans;
return 0;
}
随机数据生成
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
return (long long)rand() * rand() * rand() % (r - l + 1) + l;
}
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int n = random(1000) , m = random(1000);
printf("%d %d\n" , n , m);
for(int i = 1 ; i <= n ; i++) {
for(int j = 1 ; j <= m ; j++)
printf("%d " , random(10));
putchar('\n');
}
return 0;
}
D. 【例题4】单词背诵
题目

思路
个人觉得这题和Hash关系不大
直接把输进来的单词排序,编号,用二分法把文本换成\(1\)~\(n\) 的整数,直接统计即可解决第一问(最多包含要背的单词数,设为\(ans1\))
对于第二问,我们设置指针\(i\)for(int i = 1 ; i <= m ; i++),和一个数组\(dat_j\)记录当\(1\)~\(i\)下标中编号为\(j\)的单词最晚出现时间
若当前单词个数达到\(ans1\),我们进行第二问的答案统计:设\(tmp_i=i-\min (dat_j)+1(1\leq j\leq n)\),第二问的答案即为\(tmp\)中的最小值
\(dat\)数组涉及到单点修改和全段查询,用一个改装线段树维护即可,具体实现请看代码
总复杂度\(O(n\log n)\)
代码
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <algorithm>
#define nn 1010
using namespace std;
string sread() {
string s;
char c = getchar();
while(c < 'a' || c > 'z')c = getchar();
while(c >= 'a' && c <= 'z')
s = s + c , c = getchar();
return s;
}
int n , m;
string s[nn];
int txt[100010];
int vis[100010];
int root;
int lb[400010] , rb[400010];
int ls[400010] , rs[400010];
int dat[400010];
int build(int l , int r) {//线段树
static int cnt = 1;
int c = cnt++;
lb[c] = l , rb[c] = r , dat[c] = (1 << 29);
if(l == r) return c;
int mid = (l + r) / 2;
ls[c] = build(l , mid);
rs[c] = build(mid + 1 , r);
return c;
}
#define min_(_ , __) ((_) < (__) ? (_) : (__))
void change(int p , int id , int d) {
if(lb[p] == rb[p]) {
dat[p] = d;
return;
}
int mid = (lb[p] + rb[p]) / 2;
if(id <= mid) change(ls[p] , id , d);
else change(rs[p] , id , d);
dat[p] = min_(dat[ls[p]] , dat[ rs[p]]);
}//线段树END
int main() {
cin >> n;
for(int i = 1 ; i <= n ; i++)
s[i] = sread();
sort(s + 1 , s + n + 1);
cin >> m;
for(int i = 1 ; i <= m ; i++) {
string tmp = sread();
int l = 1 , r = n;
int mid;
while(l <= r) {
mid = (l + r) / 2;
if(s[mid] == tmp) {
txt[i] = mid;
break;
}
else if(s[mid] < tmp)
l = mid + 1;
else
r = mid - 1;
}
}
// for(int i = 1 ; i <= m ; i++)
// cout << txt[i] << '\t';
int cnt = 0;
for(int i = 1 ; i <= m ; i++) {
if(!vis[txt[i]])
++cnt;
vis[txt[i]] = true;
}
cout << cnt << endl;
memset(vis , 0 , sizeof(vis));
root = build(1 , n);
int cnt2 = 0;
int minn = 0;
int ans = m;
for(int i = 1 ; i <= m ; i++) {
if(vis[txt[i]] == 0)
++cnt2 , vis[txt[i]] = true;
change(root , txt[i] , i);
if(cnt2 == cnt) {
if(ans > i - dat[root] + 1)
ans = i - dat[root] + 1;
}
}
cout << ans;
return 0;
}
E. 【例题5】子正方形
题目
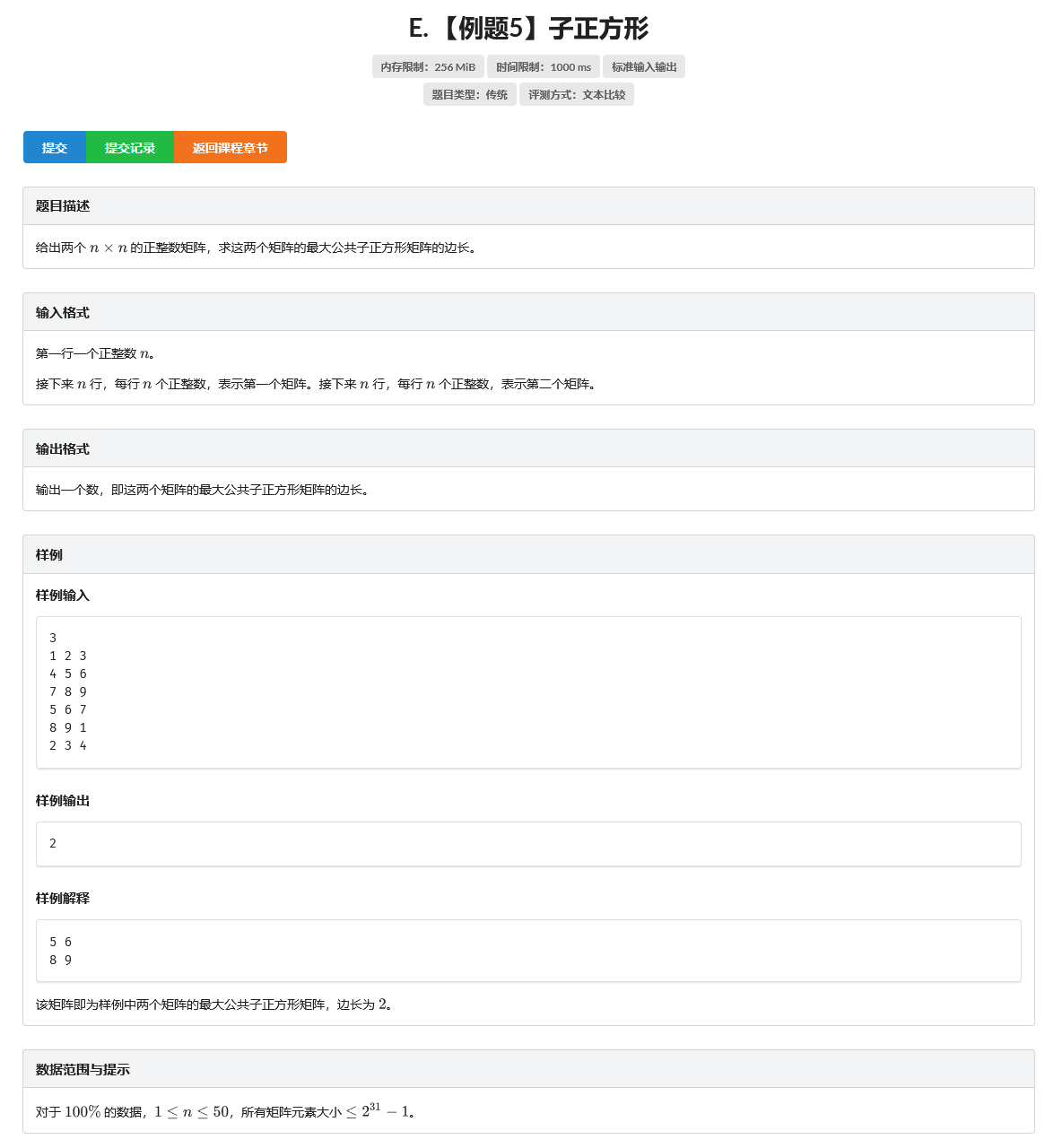
思路
比较简单的一道题,枚举两个矩阵的左上角,二分其边长,用Hash\(O(1)\)判断相等即可,总复杂度\(O(n^4\log n)\),可通过
代码
AC代码
#include <iostream>
#include <cstdio>
#define ul unsigned long long
using namespace std;
int n;
int a[2][110][110];
ul hs[2][110][110];
const ul p1 = 1331 , p2 = 13331;
ul pw1[110] , pw2[110];
inline ul getkey(int k , int x , int y , int x1 , int y1) {
return hs[k][x1][y1] - hs[k][x1][y - 1] * pw1[y1 - y + 1] - hs[k][x - 1][y1] * pw2[x1 - x + 1] + hs[k][x - 1][y - 1] * pw1[y1 - y + 1] * pw2[x1 - x + 1];
}
bool check(int len , ul key) {
if(len == 0) return true;
int m = n - len + 1;
for(int i = 1 ; i <= m ; i++)
for(int j = 1 ; j <= m ; j++)
if(key == getkey(1 , i , j , i + len - 1 , j + len - 1))
return true;
return false;
}
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int main() {
pw1[0] = pw2[0] = 1;
for(int i = 1 ; i <= 60 ; i++)
pw1[i] = pw1[i - 1] * p1 , pw2[i] = pw2[i - 1] * p2;
n = read();
for(int k = 0 ; k <= 1 ; k++)
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++)
a[k][i][j] = read();
for(int k = 0 ; k <= 1 ; k++) {
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++)
hs[k][i][j] = hs[k][i][j - 1] * p1 + a[k][i][j];
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++)
hs[k][i][j] += hs[k][i - 1][j] * p2;
}
int ans = 0;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= n ; j++) {
int l = 0 , r = n - i + 1;
if(r > n - j + 1)
r = n - j + 1;
int mid;
while(l < r) {
mid = (l + r) / 2;
if((l + r) & 1)
++mid;
if(check(mid ,
getkey(0 , i , j , i + mid - 1 , j + mid - 1)))
l = mid;
else
r = mid - 1;
}
if(l > ans)
ans = l;
}
cout << ans;
return 0;
}
随机数据生成
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l =1 ) {
return (long long)rand() * rand() * rand() % (r - l + 1) + l;
}
int main() {
unsigned seed;
cin >> seed;
seed *= time(0);
srand(seed);
int n = random(50);
cout << n << '\r';
for(int k = 0 ; k <= 1 ; k++)
for(int i = 1 ; i <= n ; i++) {
for(int j = 1 ; j <= n ; j++)
printf("%d " , random(10 , 0));
putchar('\r');
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号