「基础算法」第3章 二分算法课堂过关
「基础算法」第3章 二分算法课堂过关
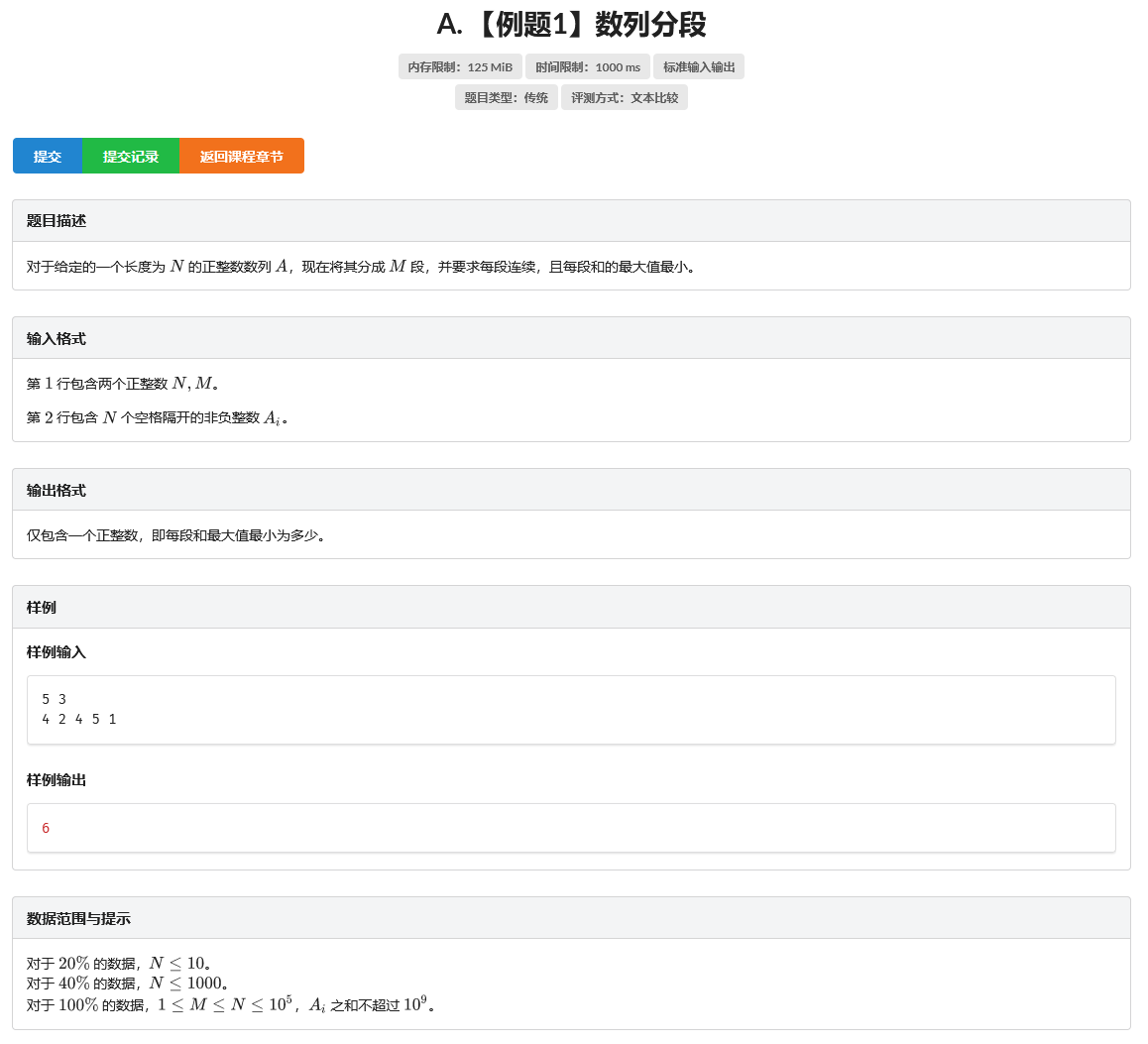
A. 【例题1】数列分段
题目
思路
挺简单的一道题,看到"最大值最小"就知道基本是二分答案+贪心(其实看到专题也应该知道)
二分枚举最小的最大值,然后:
bool check(int maxn) {
int cnt = 1;
int sum = 0;
for(int i = 1 ; i <= n ; i++) {
if(a[i] > maxn) return false;//l如果取的是a中的最大值,应该不用此特判
if(sum + a[i] > maxn) //如果当前值和前面的划分为同一段会超过限制
++cnt , sum = 0;//则把重新开一段
sum += a[i];
}
return cnt <= m;//是否能在m段以内(包含m)划分,使每段之和的最大值不超过maxn
}
代码
#include <iostream>
#include <cstdio>
#define nn 100010
using namespace std;
int read() {
int re = 0 ; bool sign = 0 ; char c;
do if((c = getchar()) == '-') sign = 1; while(c < '0' || c > '9');
while(c >= '0' && c <= '9') re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sign == 0 ? re : -re;
}
int n , m;
int a[nn];
bool check(int maxn) {
int cnt = 1;
int sum = 0;
for(int i = 1 ; i <= n ; i++) {
if(a[i] > maxn) return false;//l如果取的是最大值,应该不用此特判
if(sum + a[i] > maxn)
++cnt , sum = 0;
sum += a[i];
}
return cnt <= m;
}
int main() {
n = read();
m = read();
int l = ( 1 << 29) , r = 0;
for(int i = 1 ; i <= n ; i++) {
a[i] = read();
if(l > a[i])//这里l应该是取最大值,当时写错了,就懒得改了
l = a[i];
r += a[i];
}
while(l < r) {
int mid = (l + r) / 2;
if(check(mid))
r = mid;
else
l = mid + 1;
}
cout << l ;
return 0;
}
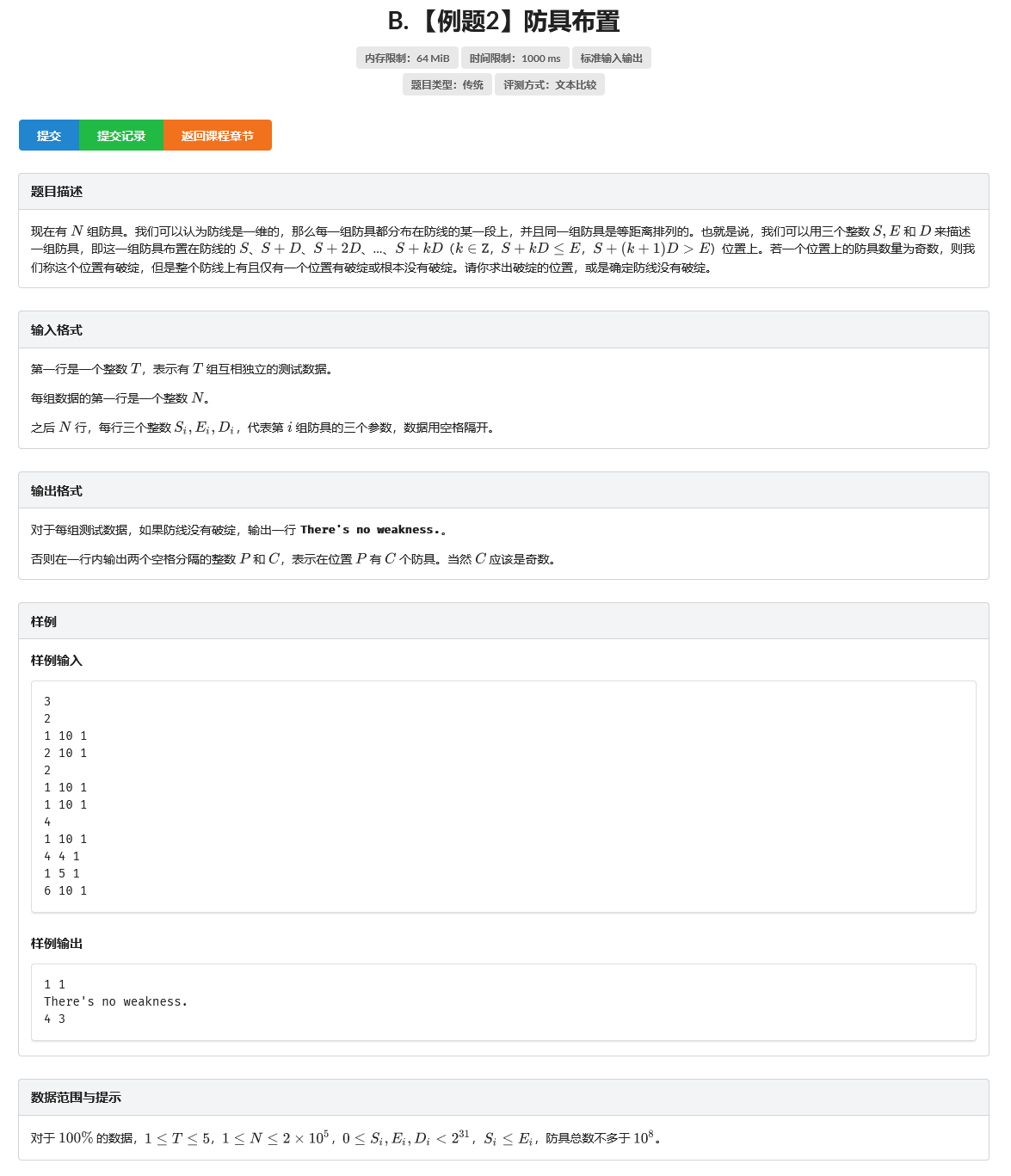
B. 【例题2】防具布置
题目
思路
题目里面很重要的一句话就是:
但是整个防线上有且仅有一个位置有破绽或根本没有破绽
这决定了我们要用二分解题
我们二分举这个"破绽"的位置(设这个为\(pos\)),计算出0~pos之间"防具"的数量(设为\(sum\)),如果\(sum\)为奇数,则说明"破绽"在pos的左边(或者就是pos),否则在pos右边.
至于如何计算"防具"的数量,就自己慢慢思考吧
更多问题,代码见
代码
#include <iostream>
#include <cstdio>
#define nn 200010
#define ll long long
#define uni long long
using namespace std;
ll read() {
ll re = 0;
bool sign = 0;
char c;
do
if ((c = getchar()) == '-')
sign = 1;
while (c < '0' || c > '9');
while (c >= '0' && c <= '9') re = (re << 1) + (re << 3) + c - '0', c = getchar();
return sign == 0 ? re : -re;
}
int n, m;
ll s[nn], e[nn], d[nn];
#define min_(_, __) (_ < __ ? _ : __)
bool check(ll pos) {//统计0~pos位置的防具数量
ll sum = 0;
for (int i = 1; i <= n; i++) {
if (s[i] <= pos) {
sum += (min_(pos, e[i]) - s[i]) / d[i] + 1u;
}
}
return (sum & 1) == 0;
}
signed main() {
ll T;
T = read();
while (T--) {
n = read();
ll l = 0, r = (1ll << 32);
for (int i = 1; i <= n; i++) {
s[i] = read(), e[i] = read(), d[i] = read();
}
if (check(r)) {//没有破绽的情况(全段的"防具"数量和为偶数)
puts("There's no weakness.");
continue;
}
while (l < r) {
ll mid = (l + r) / 2;
if (check(mid))
l = mid + 1;
else
r = mid;
}
cout << l << ' ';
ll sum = 0;
for (int i = 1; i <= n; i++) {//计算l位置的防具数量
if (s[i] <= l && e[i] >= l && (l - s[i]) % d[i] == 0)
sum++;
}
cout << sum << endl;
}
return 0;
}
C. 【例题3】最大均值
题目
思路
设平均数为x,按照题目的要求
\[\frac{ \sum_{i=l}^{r} a_i}{r-l+1} \geq x (r-l+1\geq m)
\]
要让x最大化
不难想到,原式可以变成这样:
\[\sum _{i=l}^{r}(a_i-x) \geq 0 (r-l+1\geq m)
\]
所以,我们考虑二分枚举x,把a中的数全部减去x,存在b中,判断b中是否有一段长度大于等于m的区间,使得区间内数的和大于等于0
那问题来了,怎么判断呢(看了波题解)
首先,求出b的前缀和数组sum
然后,枚举每一个i,找到
\[sum_i - sum_j (0 \leq j \leq i-m)
\]
的最大值,判断其是否大于等于0,因此,我们最小化\(sum_j\),就有了\(minv\):
minv维护的是:
\[\min\{sum_{j}\}(0\leq j\leq i-m)
\]
随着i的增长,j的取值范围往右延伸一位,我们只需将minv和新增的一个比较即可
bool check(double aver) {
for(int i = 1 ; i <= n ; i++)//求出b及其前缀和
sum[i] = sum[i - 1] + (b[i] = a[i] - aver);
double minv = 1e10 , ans = -1e10;//ans找最大值
for(int i = m ; i <= n ; i++) {
if(minv > sum[i - m])
minv = sum[i - m];
if(ans < sum[i] - minv)
ans = sum[i] - minv;
}
return ans >= 0;
}
代码
#include <iostream>
#include <cstdio>
#define nn 100010
using namespace std;
int read() {
int re = 0 ; bool sign = 0 ; char c;
do if((c = getchar()) == '-') sign = 1; while(c < '0' || c > '9');
while(c >= '0' && c <= '9') re = (re << 1) + (re << 3) + c - '0' , c = getchar();
return sign == 0 ? re : -re;
}
int n , m;
double a[nn] , b[nn];
double sum[nn];
bool check(double aver) {
for(int i = 1 ; i <= n ; i++)
sum[i] = sum[i - 1] + (b[i] = a[i] - aver);
double minv = 1e10 , ans = -1e10;
for(int i = m ; i <= n ; i++) {
if(minv > sum[i - m])
minv = sum[i - m];
if(ans < sum[i] - minv)
ans = sum[i] - minv;
}
return ans >= 0;
}
int main() {
n = read();
m = read();
double l = 1e6 , r = -l;
for(int i = 1 ; i <= n ; i++) {
a[i] = (double)read();
if(l > a[i])
l = a[i];
if(r < a[i])
r = a[i];
}
while(r - l > 1e-5) {
double mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
cout << int(r * 1000);
return 0;
}




