YbtOJ:NOIP2020 模拟赛B组 Day10

代码对拍程序见https://www.cnblogs.com/dream1024/p/14051523.html

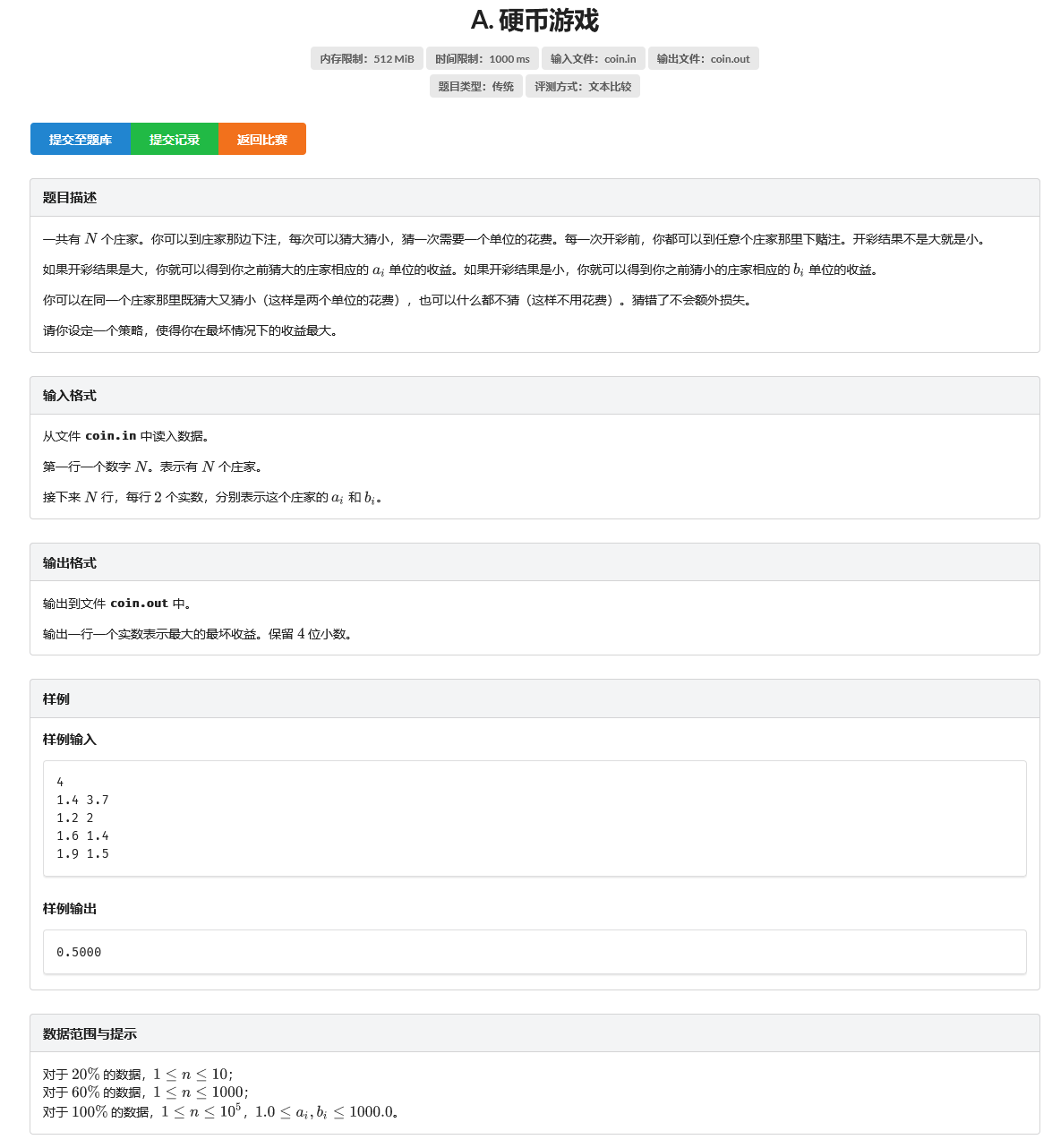
A. 硬币游戏

题目

思路

咋一看挺吓人的,其实并不难的一道题

方法一:DFS

不用多说,每个庄家4种情况,时间复杂度\(O(4^n)\),期望20分

代码

#include <iostream>
#include <cstdio>
#define min_(_,__) (_ < __ ? _ : __)
#define nn 100010
using namespace std;
void flread(double &a) {
	a = 0;
	char c = getchar();
	while(c < '0' || c > '9')c = getchar();
	while(c >= '0' && c <= '9')
		a = a * 10.0 + 1.0 * (c - '0'),
		c = getchar();
	if(c == '.') {
		c = getchar();
		double x = 0.1;
		while(c >= '0' && c <= '9') {
			a = a + (c - '0') * 1.0 * x;
			x /= 10;
			c = getchar();
		}
	}
}
int n;
double ans;
double a[nn] , b[nn];
double suma , sumb;
int ope[nn] , ansop[nn];//这两个其实没什么用,只是为了方便我理解答案而添加的
void dfs(int x , double cost) {
	if(x == n + 1) {
		double tmp = (suma < sumb ? suma : sumb) - 1.0 * cost;
		if(ans < tmp) {
			ans = tmp;
			for(int i = 1 ; i <= n ; i++)
				ansop[i] = ope[i];
		}
		return;
	}
ope[x] = 0;
	dfs(x + 1 , cost);//不猜 
	suma += a[x];
ope[x] = 1;
	dfs(x + 1 , cost + 1);//猜小 
	sumb += b[x];
ope[x] = 2;
	dfs(x + 1 , cost + 2);//猜大猜小 
	
	suma -= a[x];
ope[x] = 3;
	dfs(x + 1 , cost + 1);//猜大 
	sumb -= b[x];
}
int main() {
	cin >> n;
	for(int i = 1 ; i <= n ; i++)
		flread(a[i]) ,flread(b[i]);
	dfs(1 , 0);
	printf("%.4f\n" , ans);
//	for(int i = 1 ; i <= n ; i++)
//		cout << ansop[i] << '\t';
	return 0;
}

方法二:贪心

现将a,b两个数组从大到小排序,并求出前缀和,枚举下注的次数,用O(n)的时间求出在该赌注数量下的最优解,时间复杂度\(O(n^2)\)期望通过60%

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#define nn 100010
#define fabs(_) (_ < 0 ? -_ : _)
#define min_(_ , __) (_ < __ ? _ : __)
using namespace std;
bool cmp(double a , double b){return a > b;}
void flread(double &a) {
	a = 0;
	char c = getchar();
	while(c < '0' || c > '9')c = getchar();
	while(c >= '0' && c <= '9')
		a = a * 10.0 + 1.0 * (c - '0'),
		c = getchar();
	if(c == '.') {
		c = getchar();
		double x = 0.1;
		while(c >= '0' && c <= '9') {
			a = a + (c - '0') * 1.0 * x;
			x /= 10;
			c = getchar();
		}
	}
}
int n;
double ans;
double a[nn] , b[nn];
double suma[nn] , sumb[nn];//前缀和
double count(int x) {
	int tmp = min_(x , n);
//	cout << tmp << endl;
	double delta = 0;
	double k = 0;
	for(int i = 0 ; i <= tmp ; i++)//枚举猜大的次数
		if(min_(suma[i] , sumb[x - i]) > k)
			k = min_(suma[i] , sumb[x - i]);
	return k;
}
int main() {
	cin >> n;
	for(int i = 1 ; i <= n ; i++)
		flread(a[i]) ,flread(b[i]);
	sort(a + 1 , a + n + 1 , cmp);
	sort(b + 1 , b + n + 1 , cmp);
	for(int i = 1 ; i <= n ; i++)
		suma[i] = suma[i - 1] +  a[i] , sumb[i] = sumb[i - 1] + b[i];
	
	double ans = 0;
	for(int i = 0 ; i <= 2 * n ; i++) {//枚举下注次数
		double tmp = count(i) - 1.0 * i;
		
		if(tmp > ans)
			ans = tmp;
	}
	printf("%.4f" , ans);
	return 0;
}

方法三:二分+贪心

在方法二的基础上,我们不难想到,最后的count函数要找的就是\(\min \{^{suma_i}_{sumb_{x-i}}\)的最大值,由于前缀和数组又是递增的,所以我们考虑二分找一个i,满足\(suma_i<sumb_{x-i} \and suma_{i+1}>=sumb_{x-i-1}\),时间复杂度\(O(n\log n)\)~~(只要不是老人机就能过)~~

代码

double count(int x) {//其他部分和方法二一模一样
	int l , r = min_(x , n);
	l = x > n ? x - n : 0;
	int tmp = r;
//	cout << tmp << endl;
	while(l < r) {
		int mid = (l + r) / 2;
		if((l + r) & 1)
			mid++;
		if(suma[mid] > sumb[x - mid])
			r = mid - 1;
		else
			l = mid;
	}
//	cout << l << endl;
	if(suma[l] == sumb[x - l])return suma[l];
	double p = min_(suma[l] , sumb[x - l]);
	double q = (l + 1 <= n && x - l + 1 >= 0) ? (min_(suma[l + 1] , sumb[x - l - 1])) : -999;
	return p > q ? p : q;
}

官方题解

随机数据生成代码

#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
	return r == l ? l : (long long)rand() * rand() % (r - l) + l;
}
void frand() {
	printf("%d.%d" , //*
	random(3) == 1 ? random(5) : 1/*/random(1000)//*/
	 , random(100));
}
int main() {
	unsigned seed;
	cin >> seed;
	seed *= time(0);
	srand(seed);
	
	int n = random(1e4);
	printf("%d\n" , n);
	for(int i = 1 ; i <= n ; i++) {
		frand();
		putchar(' ');
		frand();
		putchar('\n');
	}
	
	return 0;
}

B. 开采矿物

题目

洛谷原题

思路

蒟蒻能写的代码,大佬能想的思路qwq

这题和容易让人想到DP,奈何按1~n的顺序DP是有后效性的,所以我们换一个思路:按从n到1的顺序DP

具体地,设\(f_i\)表示依次经过i~n的最大化净收入

易得状态转移:

ty[i]==1:

\[f_i=\max\{^{f_{i+1}}_{x_i\cdot w+f_{i+1}\cdot (1.0 - 0.01 \cdot k)} \]

ty[i]==2:

\[f_i=\max\{^{f_{i+1}}_{-x_i\cdot w+f_{i+1}\cdot (1.0 + 0.01 \cdot c)} \]

代码

#include <iostream>
#include <cstdio>
#define max_(_ , __) (_ > __ ? _ : __)
using namespace std;
int read() {
	int re = 0 , sig = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-')sig = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
		re = (re << 1) + (re << 3) + c - '0',
		c = getchar();
	return re * sig;
}
int n , k , c , w;
int x[100010];
int ty[100010];
double f;
int main() {
	freopen("exploit.in" , "r" , stdin);
	freopen("exploit.out" , "w" , stdout);
	
	n = read() , k = read() , c = read() , w = read();
	for(int i = 1 ; i <= n ; i++)
		ty[i] = read() , x[i] = read();
	for(int i = n ; i > 0 ; i--)
		if(ty[i] == 1)
			f = max_(f , x[i] * w + f * (1.0 - 0.01 * k));
		else
			f = max_(f , -x[i] * w + f * (1.0 + 0.01 * c));
	printf("%.2f" , f);
	return 0;
}

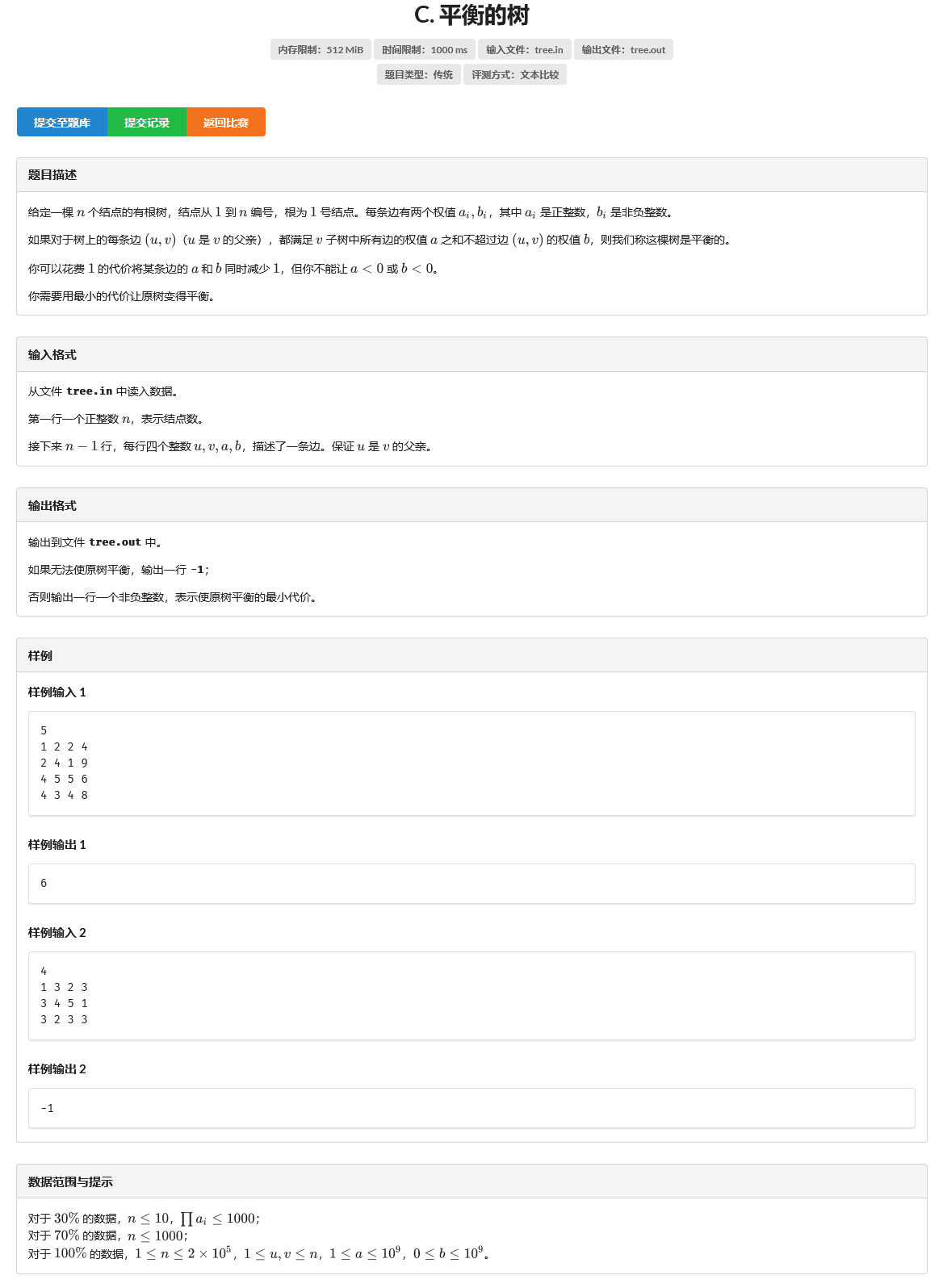
C. 平衡的树

题目

思路

其实不难的一道题,就是看着比较吓人

直接考虑DFS遍历,对于当前结点x,我们需要返回以x的根的子树的a值之和,以及以x为根的整颗子树最多可以进行多少次a,b同时减1的操作,我这里用的是pair捆绑两个值

a的值之和很好求,那问题是可以进行操作的次数(设为con)

看了下别人的代码,是直接\(con+\min (a,b)\) 而我的比较复杂:

		int b_ = b;
		if(a < b)b -= a;
		else	b = 0;
		if(suma - con > b) b = suma - con;//suma-con:子树能够达到的最小的suma
		res_con += con + b_ - b;

两者都能AC这道题目,两者不统一的概率也非常低,我对拍了上千组数据才得到一组不统一的数据(见本题末尾),但是我觉得我是对的

对于其它问题,代码解释

代码

AC代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#define nn 200010
#define int long long//原谅我一开始没注意,后来懒得一个个改long long
using namespace std;
int read() {
	int re = 0 , sig = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-')sig = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
		re = (re << 1) + (re << 3) + c - '0',
		c = getchar();
	return re * sig;
}
struct ednode{
	int to , nxt , a , b;
}ed[nn * 2];
int head[nn];
void addedge(int u , int v , int a , int b) {
	static int top = 1;
	ed[top].a = a , ed[top].b = b , ed[top].to = v , ed[top].nxt = head[u] , head[u] = top;
	++top;
}

int n;
int ope;
pair <int,int> dfs(int x) {
	int res_con = 0 , res_suma = 0;
	for(int i = head[x] ; i ; i = ed[i].nxt) {
		int to = ed[i].to , a = ed[i].a , b = ed[i].b;
		pair <int,int> tmp = dfs(to);
		int con = tmp.first , suma = tmp.second;
		
		
		if(suma - con > b) {
			puts("-1");
//			cout << x << "\t" << to << endl;
			exit(0);
		}
		if(suma > b) {
			con -= suma - b;
			ope += suma - b;
			suma = b;
		}
/*		else {
			con += b - suma;
			if(a - (b - suma) < 0)
				con -= b - suma - a;
		}//*/
		int b_ = b;
		if(a < b)b -= a;
		else	b = 0;
		if(suma - con > b) b = suma - con;
		res_con += con + b_ - b;
		res_suma += a + suma;
	}
	return make_pair(res_con , res_suma);
}
signed main() {
//	freopen("tree.in" , "r" , stdin);
//	freopen("tree.out" , "w" , stdout);
	
	n = read();
	for(int i = 1 ; i < n ; i++) {
		int u = read() , v = read() , a = read() , b = read();
		addedge(u , v , a , b);
	}
	dfs(1);
	cout << ope;
	return 0;
}

随机数据生成代码

#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
	return r ==l ? l : (long long)rand() * rand() % (r - l) + l;
}
int main() {
	unsigned seed;
	cin >> seed;
	seed *= time(0);
	srand(seed);
	
	int n = random(100000);
	cout << n << endl;
	for(int i = 2 ; i <= n ; i++) {
		printf("%d %d %d %d\n" , random(i - 1) , i , random(100) , random(1500));
	}
	return 0;
}

hack数据

421
1 2 28 630
1 3 58 57
1 4 67 132
1 5 15 1043
2 6 13 313
4 7 34 678
1 8 70 1291
2 9 1 721
1 10 75 6
1 11 38 173
7 12 55 1304
8 13 63 897
11 14 80 682
13 15 79 990
9 16 1 740
7 17 91 934
3 18 14 632
9 19 66 1482
13 20 9 1213
18 21 88 328
9 22 23 855
11 23 61 806
8 24 82 78
23 25 95 404
3 26 45 381
19 27 55 1220
14 28 78 1014
7 29 12 742
2 30 56 600
15 31 13 64
1 32 43 1205
17 33 48 894
17 34 79 487
13 35 2 182
15 36 87 1053
9 37 10 89
17 38 37 978
10 39 32 713
9 40 94 19
19 41 28 775
31 42 88 1164
11 43 22 37
34 44 11 152
41 45 11 1206
41 46 1 124
16 47 40 1059
25 48 45 440
12 49 94 593
14 50 37 657
25 51 65 1301
21 52 73 300
7 53 63 315
41 54 17 1
25 55 7 64
23 56 65 1013
43 57 22 201
22 58 34 1163
4 59 16 40
51 60 41 331
55 61 33 1133
5 62 7 236
42 63 73 798
21 64 33 665
52 65 13 1448
53 66 66 836
65 67 38 751
44 68 10 383
12 69 8 126
19 70 10 385
5 71 82 405
50 72 1 178
4 73 1 911
71 74 31 904
69 75 34 1430
28 76 55 357
17 77 1 1272
9 78 73 490
55 79 51 1273
12 80 56 1084
38 81 10 1084
51 82 45 1212
77 83 12 821
49 84 55 583
15 85 1 129
53 86 90 49
83 87 91 651
47 88 82 1333
12 89 7 1492
37 90 34 436
34 91 27 57
1 92 91 539
72 93 67 828
25 94 64 447
61 95 31 968
13 96 59 60
66 97 97 909
49 98 56 637
57 99 61 1441
93 100 31 326
22 101 29 559
83 102 65 185
83 103 73 203
17 104 41 244
55 105 21 947
70 106 16 503
51 107 80 579
67 108 33 752
55 109 16 346
91 110 28 866
15 111 54 868
81 112 90 687
82 113 28 1114
99 114 34 1302
29 115 52 372
27 116 34 316
35 117 43 138
22 118 19 1440
76 119 1 445
115 120 49 762
24 121 41 859
67 122 31 764
95 123 21 1422
21 124 7 933
123 125 72 1499
25 126 40 1252
125 127 99 855
1 128 55 634
109 129 32 1249
108 130 6 739
72 131 19 177
113 132 52 716
47 133 58 1128
26 134 1 915
102 135 75 382
38 136 35 649
23 137 67 650
91 138 62 7
98 139 46 97
71 140 70 372
86 141 5 1319
71 142 50 1361
75 143 79 86
47 144 55 437
115 145 1 210
66 146 47 1447
7 147 40 778
23 148 52 12
109 149 76 500
121 150 72 461
46 151 82 1254
91 152 58 1145
65 153 1 697
35 154 10 933
58 155 52 205
95 156 61 1111
45 157 26 1139
16 158 94 118
35 159 69 1151
28 160 49 1217
13 161 12 1486
89 162 1 1089
129 163 37 502
73 164 96 618
134 165 30 982
111 166 37 1214
130 167 41 339
55 168 90 905
98 169 16 1088
106 170 27 1384
119 171 41 440
95 172 72 72
153 173 82 228
119 174 43 42
72 175 97 1143
110 176 4 603
151 177 98 1497
15 178 76 716
110 179 10 994
113 180 1 740
105 181 83 386
177 182 40 636
125 183 7 1285
1 184 40 449
76 185 46 56
177 186 67 205
75 187 59 889
79 188 12 535
169 189 94 280
1 190 59 575
78 191 28 348
57 192 10 901
22 193 91 218
139 194 88 1326
16 195 2 1204
142 196 91 745
49 197 51 1188
107 198 66 1404
74 199 43 680
149 200 25 1450
9 201 24 953
181 202 89 1024
77 203 5 852
39 204 33 1107
183 205 12 154
109 206 91 1100
181 207 64 795
101 208 82 671
58 209 30 1343
179 210 92 377
152 211 49 1091
113 212 88 706
46 213 5 1470
4 214 98 877
167 215 23 1184
213 216 46 1199
16 217 18 672
84 218 13 1280
137 219 7 446
176 220 89 724
94 221 67 320
129 222 43 1050
128 223 19 273
75 224 70 298
22 225 55 263
219 226 43 313
209 227 34 1275
213 228 91 1287
12 229 17 162
59 230 67 855
163 231 59 698
67 232 79 674
163 233 1 409
146 234 16 1281
226 235 49 1031
121 236 91 1170
121 237 1 160
89 238 2 1170
58 239 85 1156
230 240 18 633
182 241 56 1345
49 242 61 1002
102 243 67 1404
183 244 36 120
62 245 13 270
116 246 61 648
192 247 43 659
202 248 57 1076
103 249 85 1188
235 250 11 909
3 251 34 663
137 252 83 953
134 253 31 175
91 254 54 879
28 255 73 474
80 256 64 602
94 257 78 1174
75 258 19 1014
72 259 22 613
49 260 77 1427
160 261 1 882
246 262 94 192
235 263 61 1275
167 264 23 607
144 265 4 1
73 266 43 842
76 267 78 218
84 268 34 780
34 269 79 549
221 270 70 1023
15 271 43 1088
49 272 91 736
262 273 34 796
72 274 38 1244
208 275 75 351
270 276 78 214
243 277 47 1213
133 278 67 26
11 279 40 1345
145 280 37 1259
217 281 44 899
113 282 22 1326
241 283 73 524
145 284 1 1448
144 285 10 1403
57 286 61 63
44 287 34 801
183 288 94 61
209 289 82 461
118 290 25 330
151 291 96 945
201 292 64 935
45 293 10 1209
287 294 28 1142
230 295 67 175
277 296 14 292
102 297 84 390
198 298 53 83
157 299 4 1202
89 300 59 573
57 301 14 815
64 302 76 1055
7 303 5 195
40 304 43 825
37 305 54 57
303 306 14 1120
165 307 27 304
87 308 67 1116
181 309 30 462
295 310 83 360
103 311 58 188
255 312 82 626
251 313 30 240
257 314 27 1239
166 315 16 701
205 316 31 138
136 317 1 867
217 318 50 116
52 319 73 370
310 320 39 236
111 321 9 46
184 322 91 308
304 323 61 340
93 324 34 269
115 325 4 17
91 326 1 124
223 327 10 518
172 328 6 241
229 329 55 616
150 330 90 915
58 331 98 551
73 332 94 1032
119 333 19 538
167 334 8 210
25 335 15 215
171 336 19 1
164 337 38 48
286 338 37 1417
307 339 7 1425
259 340 1 400
146 341 23 1340
35 342 45 1171
105 343 34 295
253 344 7 35
185 345 84 854
177 346 27 1129
33 347 45 899
88 348 13 788
279 349 92 839
195 350 71 433
316 351 19 380
132 352 12 439
301 353 52 676
223 354 64 459
167 355 57 349
325 356 62 972
296 357 74 862
133 358 3 686
266 359 90 1315
293 360 82 346
104 361 15 192
126 362 78 1495
47 363 56 478
71 364 28 889
301 365 58 1019
94 366 52 595
154 367 34 85
118 368 36 330
69 369 22 585
91 370 46 1336
307 371 61 1247
75 372 56 188
1 373 12 48
349 374 22 685
372 375 64 1485
298 376 94 279
155 377 21 106
161 378 1 1316
372 379 80 997
156 380 28 1436
135 381 97 1302
357 382 84 1052
347 383 82 608
67 384 46 1328
183 385 92 95
347 386 52 1101
57 387 27 372
49 388 10 1132
292 389 99 807
53 390 91 64
188 391 41 1429
366 392 55 844
320 393 44 943
244 394 41 1495
274 395 82 326
188 396 18 640
145 397 54 870
145 398 64 645
148 399 55 390
46 400 16 533
175 401 22 962
235 402 92 350
77 403 73 537
149 404 88 791
20 405 92 331
317 406 23 1257
64 407 56 1349
343 408 82 492
135 409 56 269
370 410 23 1290
105 411 85 1190
61 412 43 1226
31 413 44 535
78 414 96 171
101 415 98 568
40 416 58 105
59 417 53 141
394 418 39 342
300 419 76 407
21 420 1 1020
343 421 56 318

D. 挺好序列

题目

思路

听说比较复杂,我也没做

posted @ 2020-11-30 17:04 追梦人1024 阅读(520) 评论(0) 编辑收藏举报

刷新页面返回顶部