P6824 「EZEC-4」可乐[详解]

目录

• 题目
• 思路
• 代码

题目

传送门

一道很好的trie练手题

思路

如果有更好的优化方法欢迎留言哦~~

这里写的可能比较难懂,结合代码食用效果更佳

根据k和a的大小(1e6),可知它们在二进制下大概就去到20位的样子,为了保险,我们取21位

对于每一个a,我们建一棵深度为21(不计算根)的trie,结点为0或1,从高位到低位存储a

例:

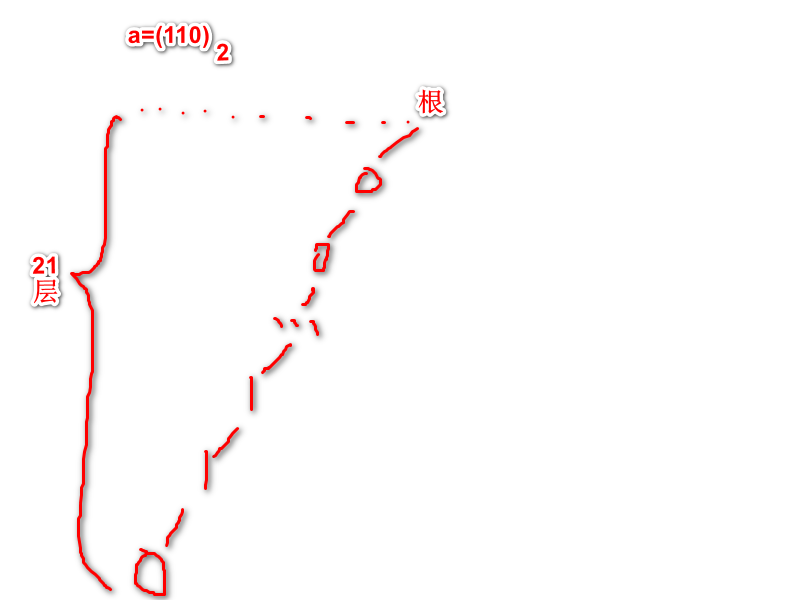
我们改造trie中的end[]为cnt[]表示以某个结点为结束点的数的个数,并对cnt[]求前缀和,放在sum[]中,注意:树形结构的前缀和和差分基本都是自底向上的(这里不细讲),另外开一个数组dep[],表示某个结点的子结点是所存储的数从低到高的第几位(从0数起),以上图为例,根的dep为21,最底层dep无意义(这里表达地不太好理解,结合代码看效果可能更佳)

接着我们从1到2^21枚举每一个可能的x(这也是这个解法最耗时间的地方)

对于一个trie结点p,假设"根到这个结点的路径组成的数"和"k从高到低相同位数下的数"相同,如果k的下一位是1,若我们下一位异或的结果是0,则剩下的数取0或1都可以(因为是从高位到低位讨论的),直接利用sum计算即可,如果k的下一位和我们下一位异或得到的结果相同,则递归到下一层讨论

很显然,对于每一个x,我们统计答案时在树上走的路径是一条长度为21链

因此,总复杂度为O(2^21 * 21)

有一些细节问题是讲不清楚的,需要自己慢慢摸索,自己搞清楚后,你就发现对trie的理解加深了不少

代码

#include <iostream>
#include <cstdio>
#define nn (1 << 22)
using namespace std;
int read() {
	int re = 0;
	char c = getchar();
	while(c < '0' || c > '9')c = getchar();
	while(c >= '0' && c <= '9')
		re = (re << 1) + (re << 3) + c - '0',
		c = getchar();
	return re;
}
int n , k;
int x;

int trie[nn][3];
int cnt[nn] , sum[nn] , dep[nn];
void insert(int a) {//插入
	static int top = 1;
	int p = 1;
	for(int i = 21 ; i >= 0 ; i--) {
		int tmp = ((a >> i) & 1);
		dep[p] = i;
		if(trie[p][tmp] == 0)
			trie[p][tmp] = ++top;
		p = trie[p][tmp];
	}
	cnt[p]++;
}
void dfs(int p) {//求sum数组
	if(p == 0)return;
	dfs(trie[p][0]);
	dfs(trie[p][1]);
	sum[p] = sum[trie[p][0]] + sum[trie[p][1]] + cnt[p];
}
int cal(int p) {
	if(p == 0)return 0;
	int res = 0;
	if(((k >> dep[p]) & 1) == 1) {
		res += sum[trie[p][0 ^ ((x >> dep[p]) & 1)]];
		res += cal(trie[p][1 ^ ((x >> dep[p]) & 1)]);
	}
	else 
		res += cal(trie[p][0 ^ ((x >> dep[p]) & 1)]);
	return res;
}

int main() {
	n = read();	k = read();
	for(int i = 1 ; i <= n ; i++)
		insert(read());
	int maxn = (1 << 21);
	dfs(1);
	int ans = 0;
	for(x = 0 ; x <= maxn ; x++) {
		int tmp = cal(1);
		if(tmp > ans)
			ans = tmp;
	}
	cout << ans;
	return 0;
}