KMP算法详解
upd on 2021/4/1 优化一些细节
声明:本文的字符串下标均从1开始,对于某个字符串a,a.substr(i,j)表示a从第i位开始,长度为j的字串
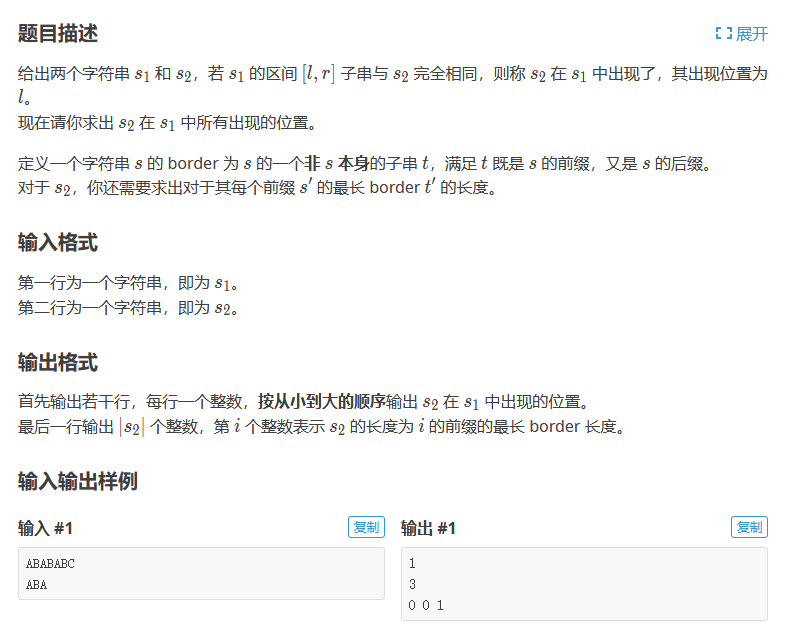
模板题
KMP算法的大致原理
个人认为其他博客已经讲得很好,这里简单讲,把重点放在next数组上
先推几篇博客:
首先,我们把模板题中的\(s_1\)串称为文本串,重命名为\(s\),\(s_2\)称为模式串,重命名为\(t\)(本文中不区分s与t的大小写)
设\(n\)为\(s\)的长度,\(m\)为\(t\)的长度(会在代码片中出现)
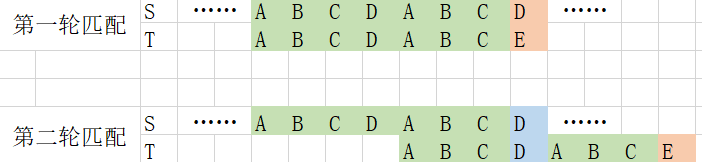
看图,在第一轮匹配中,匹配到了一个不相等的位置,如果用暴力,那就是从头再匹配,但是可以看到\(t\)串中有一段重复的“ABC”,无需重复匹配,所以第二轮直接跳到如图所示的位置比较两个蓝色的部分
这就是KMP算法的大致思路
next数组
定义
看了KMP的大致原理,相信大家都产生了疑问:我怎么知道要让T串跳到哪个位置呢?这就要用到next数组了,这是KMP的核心,也是难点
先不用管怎么求next数组,看定义(我自己写的):
令\(j=next_i\),则有\(j<i\)且\(t.substr(1,j)==t.substr(i-j+1,i)\),且对于任意\(k(j<k<i)\),\(t.substr(1,k)≠t.substr(i-k+1,k)\)
也就是说,next[i]表示“T中以i结尾的非前缀字串”与“T的前缀”能匹配的最长长度,当不存在这样的j时,next[i]=0
举个例子:
若T="ABCDABCE",则对应的next={0 0 0 0 1 2 3 0}
应用
根据next数组的定义,next中存储的是长度,但是由于它是T的某个前缀字串的长度,我们也可以将next当做下标使用(一定要弄清楚,不然后面很蒙)
仍然用上面的图片真懒呐

设S的指针为i,T的指针为j,表示当前完成匹配的位置(也就是说S[i]和T[j]是相等的)
第一轮匹配中,当\(j==7\)时,我们发现\(t\)的下一位和\(s\)的下一位不等,但是\(t\)的第57位和13位是一样的,即next[7]=3,所以我们需要将\(t\)的指针(j)跳到第3位,也就是j=next[j],这里有一些细节不是很好理解,KMP在实现时是很巧妙的,我们放到整段代码理解:
while(j != 0 && s[i] != t[j+1])
j = next[j];
if(s[i] == t[j+1])
j++;
if(j == m){//j==m标志着已经全部完成匹配
printf("%d\n",i - m + 1);
j = next[j];
}
求法
这里是整个KMP最难理解的部分,所以放到最后
先贴出代码
next[1] = 0;//初始化
for(int i = 2 , j = 0 ; i <= m ; i++){
while(j != 0 && t[j+1] != t[i])
j=next[j];//全算法最confusing的语句
if(t[j+1] == t[i])
j++;
next[i] = j;
}
考虑暴力枚举:最外层循环枚举每一位\(i\),第二层枚举next[i],里层判断第二层枚举的是否合法
显然,时间复杂度是在\(O(n^2)~O(n^3)\),还不如\(O(n\cdot m)\)的暴力匹配
优化求法:
先提前声明:求next[i]是要用到next[1~i-1]的,所以我们要从前向后顺序枚举i
定义“候选项”的概念(可能跟《算法竞赛……》的不大一样):如果j满足 t.substr(1,j)==t.substr(i-1-j-1,j)&&j<i-1则j是next[i]的一个候选项
例子:

绿色表示相等的两个字串,则j是next[i]的一个候选项,若标成蓝色的两个字符相等,则候选项j是合法的,next[i]就是所有合法的\(j\)中的最大值+1
很显然,对于next[i]而言,next[i-1]是它的候选项,但是,问题是next[next[i-1]],next[next[next[i-1]]],......都是候选项,为什么呢?还是看图:

假设next[13]=5,根据\(next\)的定义,标绿色部分是相等的,再细化一下绿色部分中相等的部分:假设next[5]=2,同理,第二行(不计最上面的下标行)的黄色部分相等,又因为绿色部分相等,我们可以得到第三行的黄色部分都是相等的,再简化为第4行,会发现:这不是和第一行一样了吗(只是长度小了)!
以此类推,可以得到next[i-1],next[next[i-1]],next[next[next[i-1]]],......都是候选项,且他们的值是从左向右递减的,因此,按照这个顺序找到第一个合法的候选值之后,我们就可以确定next[i]了
重新看一下代码:
next[1] = 0;
for(int i = 2 , j = 0 ; i <= m ; i++){
while(j != 0 && t[j+1] != t[i])//找到第一个合法的候选项
j=next[j];//缩小长度
if(t[j+1] == t[i])
j++;
next[i] = j;
}
发现,每一轮循环没有j=next[i-1]的语句。原因很简单:上一轮结束时语句next[i]=j决定了这一轮刚开始就有j==next[i-1],注意这里的前后的\(i\)不一样(都不是同一轮循环了)不要学傻了
时间复杂度
上结论:\(O(n+m)\)
以\(next\)数组的求值为例:
next[1] = 0;
for(int i = 2 , j = 0 ; i <= m ; i++){
while(j != 0 && t[j+1] != t[i])
j=next[j];
if(t[j+1] == t[i])
j++;
next[i] = j;
}
最外层显然是\(O(m)\)的,问题是里面
在while循环中,\(j\)是递减的,但是又不会变成负数,所以整个过程中,\(j\)的减小幅度不会超过\(j\)增加的幅度,而\(j\)每次才增加1,最多增加\(m\)次,故\(j\)的总变化次数不超过\(2m\),整个时间复杂度近似认为是\(O(m)\)
如果还不能理解,就想像一个平面直角坐标系,\(x\)轴为\(i\),\(y\)轴为\(j\),从原点出发,\(i\)每向右一个单位,\(j\)最多向上一个单位,\(j\)也可以往下掉(while循环),但不能掉到第四象限,\(j\)向下掉的高度之和就是while内语句执行的总次数,是绝对不会超过\(m\)的
匹配的循环与上述相近,时间为\(O(n+m)\),不再赘述
所以,总的时间复杂度为\(O(n+m)\)
模板题代码
不要问模板题输出的最后一行是什么意思,我也不知道,反正输出\(next\)数组就对了
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 1000010
using namespace std;
int sread(char s[]) {
int siz = 1;
do
s[siz] = getchar();
while(s[siz] < 'A' || s[siz] > 'Z');
while(s[siz] >= 'A' && s[siz] <= 'Z') {
++siz;
s[siz] = getchar();
}
--siz;
return siz;
}
char s[nn];
char t[nn];
int next[nn];
int n , m;
int main() {
n = sread(s);
m = sread(t);
next[1] = 0;
for(int i = 2 , j = 0 ; i <= m ; i++){
while(j != 0 && t[j+1] != t[i])
j=next[j];
if(t[j+1] == t[i])
j++;
next[i] = j;
}
for(int i = 1 , j = 0 ; i <=n ; i++){
while(j != 0 && s[i] != t[j+1])
j = next[j];
if(s[i] == t[j+1])
j++;
if(j == m){
printf("%d\n",i - m + 1);
j = next[j];
}
}
for(int i = 1 ; i <= m ; i++)
printf("%d " , next[i]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号