20201104CSP提高组训练(普通快乐&小王子&简单的打击&WC)
普通快乐
题目
题目描述
有一天,你要去找 夹克老爷 玩,但是发现他并不在家,所以你打算回家刷题,发现 绿色夹克蛤 给你制造了一个迷 宫。这个迷宫满足下面的几个性质:
由于你想回家,所以你为了让 绿色夹克蛤 快乐,你决定帮他解决一道难题。 绿色夹克蛤 现在要求你从其中任意一个奇葩点开始走,走到除了这个奇葩点以外的最近奇葩点。问选择哪一个 奇葩点开始走,路程最小。
输入格式
输入 n,m,k。
接下来的m行各3个数x,y,c,表示x,y之间有一条距离为c的边。
接着一行, k个数表示k个奇葩点。
输出格式
共一行一个数,表示答案。
输入输出样例
输入 #1
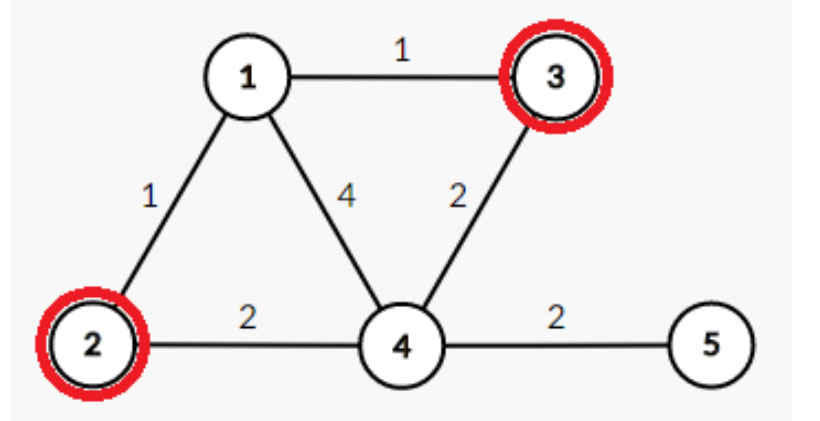
4 5 2
1 2 1
1 4 4
2 4 2
3 4 2
1 3 1
2 3
输出 #1
2
说明/提示
数据范围
对于 20%的数据, n<=1000,m<=2000
对于另外 20%的数据, 1<=c<=3
对于 100%的数据, n<=100000,m<=200000;2<=k<=n,1<=x,y<=n,1<=c<=10000
样例解释
在 Example 的图中,发现从 2 开始和从 3 开始的最短路径是 2,答案即为 2.
思路
考场:k遍SPFA20分不多说
正解O(nlog(n)):
一遍Dijkstra,没错,只需一遍!!!
将所有的"奇葩点"作为源点(距离全部设为0),dij过程中若找到距离最小的点是"奇葩点"且该最短路径不以起点为终点,那么该距离就是答案,直接输出并结束程序
但问题是:我们怎么知道一条路径是不是以起点为终点呢?
这就要我们在进行优先队列优化时捆绑3个变量:结点编号,距离,源点(即当前最短路径是从哪一个"奇葩点"出发的),其中,距离为比较的关键字
另外,题解还给出了另一种解法:
找到一对奇葩点,使得他们距离尽可能小。
两个不同的奇葩点二进制必有一位不同,那么我们二进制分组,从一组往另外一组跑最短路就可以了,时间复杂度
O(m log (n+m) log n)
不过看不太懂
代码
我的(#1+.cpp)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define nn 100010
using namespace std;
int read() {
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re * sig;
}
struct ednode{
int len , to , nxt;
}ed[1000010];
int head[nn];
inline void addedge(int u , int v , int len) {
static int top = 1;
ed[top].to = v , ed[top].len = len , ed[top].nxt = head[u] , head[u] = top;
top++;
}
bool ty[nn];
int poi[nn];
int dis[nn];
bool vis[nn];
struct qnode{
int dis , x , from;
bool operator < (const qnode &b)const{
return b.dis < dis;
}
};
qnode pus(int dis , int x , int from) {
qnode tmp;
tmp.dis = dis , tmp.x = x , tmp.from = from;
return tmp;
}
int n , m , k;
priority_queue <qnode> q;
int main() {
n = read() , m = read() , k = read();
for(int i = 1 ; i <= m ; i++){
int u , v , len;
u = read() , v = read() , len = read();
addedge(u , v , len);
addedge(v , u , len);
}
for(int i = 1 ; i <= k ; i++)
ty[poi[i] = read()] = true;
int ans;
memset(dis , 0x3f , sizeof(dis));
for(int i = 1 ; i <= k ; i++) {
dis[poi[i]] = 0;
q.push(pus(0 , poi[i] , poi[i]));
}
while(!q.empty()) {
qnode k = q.top();
q.pop();
if(vis[k.x] && !ty[k.x])
continue;
vis[k.x] = true;
if(ty[k.x] && k.from != k.x){
while(!q.empty()) {
qnode tmp = q.top();
q.pop();
}
cout << k.dis;
return 0;
}
for(int j = head[k.x] ; j ; j = ed[j].nxt) {
if(ty[ed[j].to]) {
q.push(pus(k.dis + ed[j].len , ed[j].to , k.from));
}
else if(!vis[ed[j].to] && dis[ed[j].to] > k.dis + ed[j].len) {
dis[ed[j].to] = k.dis + ed[j].len;
q.push(pus(dis[ed[j].to] , ed[j].to , k.from));
}
}
}
return 0;
}
题解(#1std.cpp)
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
int k,n;
int m;
struct edge{
int y,next,c;
}s[400010];
struct node{
int x,c;
bool operator<(const node a)const{
return c>a.c;
}
};
int first[100010],len=0;
int g[100010],dis[100010];
priority_queue<node> f;
bool tf[100010],we[100010];
int ans=1e9;
void read(int&x){
char ch=getchar();x=0;
while(ch<'0' || ch>'9') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
}
void ins(int x,int y,int c){
s[++len]=(edge){y,first[x],c};first[x]=len;
}
void solve(int x){
for(int i=1;i<=n;i++) dis[i]=1e9,tf[i]=false;
for(int i=1;i<=k;i++) if((g[i]>>x)&1) f.push((node){g[i],0}),dis[g[i]]=0;
while(!f.empty()){
node x=f.top();f.pop();
if(tf[x.x]) continue;
tf[x.x]=true;
for(int i=first[x.x];i!=0;i=s[i].next)if(dis[x.x]+s[i].c<dis[s[i].y]) {
dis[s[i].y]=dis[x.x]+s[i].c;
f.push((node){s[i].y,dis[s[i].y]});
}
}
for(int i=1;i<=k;i++) if(!((g[i]>>x)&1)) ans=min(ans,dis[g[i]]);
}
int main(){
read(n);read(m);read(k);
int x,y,c;
for(int i=1;i<=m;i++){
read(x);read(y);read(c);
ins(x,y,c);ins(y,x,c);
}
for(int i=1;i<=k;i++) read(g[i]);
for(int i=0;i<=16;i++) solve(i);
printf("%d\n",ans);
}
附:关于对拍
随机数据生成(#1random.cpp)
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
if(l == r)return l;
return (long long)rand() * rand() % (r - l) + l;
}
pair <int , int> h[1000010];
map <pair<int , int> , bool > v;
int dict[1000010];
int main() {
int n = 100000 , m = 200000 , k = random(n);
srand((unsigned)time(0));
for(int i = 1 ; i <= n ; i++)
dict[i] = i;
random_shuffle(dict + 1 , dict + n + 1);
for(int i = 2 ; i <= n ; i++) {
int x = random(i - 1);
h[i - 1] = make_pair(x , i);
v[h[i - 1]] = v[make_pair(i , x)] = 1;
}
for(int i = n ; i <= m ; i++) {
int x , y;
do{
x = random(n) , y = random(n);
}while(x == y || v[make_pair(x , y)] == 1);
h[i] = make_pair(x , y);
v[h[i]] = v[make_pair(y , x)] = 1;
}
random_shuffle(h + 1 , h + m + 1);
printf("%d %d %d\n" , n , m , k);
for(int i = 1 ; i <= m ; i++) {
printf("%d %d %d\n" , dict[h[i].first] , dict[h[i].second] , random(10000));
}
for(int i = 1 ; i <= n ; i++)
dict[i] = i;
random_shuffle(dict + 1 , dict + n + 1);
for(int i = 1 ; i <= k ; i++)
printf("%d " , dict[i]);
return 0;
}
全自动对比(#1compare.cpp)
#include <bits/stdc++.h>
using namespace std;
int main() {
while(true) {
system("#1random.exe > input.txt");
puts("finished:\trandom");
system("#1+.exe < input.txt > output.txt");
puts("finished:\t#1+");
system("#1std.exe < input.txt > output2.txt");
puts("finished:\tstd");
if(system("fc output.txt output2.txt")) {
cout << "WA\n";
system("start input.txt");
return 0;
}
}
return 0;
}
小王子
题目
题目描述
“如果我沿着这条路一直往上面去,我就可以摘到那一颗星星。”
“可是物理好难啊。”
“那我还是去炸星星好了。”
“就算是要到月亮上去罚站也没关系呀。”
十二月的风凌冽。
他站在阳台上,嘴里叼着一根从隔壁房间偷来的草莓味棒棒糖,眯着眼试图从漫天飞雪中嗅到一丝秋天的气息。黑 与白构成不分明的界限,混沌地勾勒出陌生的形状。
倒像是一堆散乱的线条。
他又眯着眼看那清凌凌的夜空。
像是那么多的星星。
随手把剩下的棍子扔向,他打了个哈欠,想起厨房里的《赢在微点》。
再看,是N颗星星牵着N-1条线。
是N-1条白色的线束缚着N颗星星。
“你为什么盯着星星看这么久?”
“我喜欢一颗小星星,所以遥望星空,试图用大脑向宇宙发送一些信号。”
“那宇宙给你反馈了吗?”
“没呢。”
“希望那颗小星星可以在宇宙来临之前,先跑到我面前哦。”
“那就换一颗嘛,天上的星星多得是。”
——可那线条好少。
——那便多一点好了。
于是他依稀看见M条黑色的线与N条白色的线交错,不重合也不缠绕。都只是轻轻地拉着那些星星,并不捆绑,连接 着两颗不同的星星,却不知怎的令他们无法脱身。
“宇宙给你反馈了吗?”
“没有。”
“那就换一颗嘛,天上的星星多得是。”
“环游整个星系,我大概找不到更亮的星星。”
——那就去摘啊。自己的星星自己摘。
——可是我的宇宙飞船可能会遇到流星,可能会用光所有的燃料。
——可是宇宙里的信号表示,那颗小星星在靠近。星河万顷,都是见面礼。
——可他有点慢啊。
——那就把他炸下来。
他看着那些不存在的线条与星星,决定用他仅有的两发导弹之中的一发去毁灭一条白线,使那些星星分成两部分。
想着他在物理书上写下:“#define 炸星星 使那些星星分成两部分”。
然后失望地发现有些时候无法成功地炸星星。
于是他决定用仅剩的一发他本决定用来保证晚年幸福的导弹去毁灭一条黑线。
不是每一个月亮都能遇到宇航员的。
但他还是想知道他有多少种使他的小星星在下一秒便出现在他怀里的方案。
可他要送什么见面礼给他的小星星呢?
他只有两发导弹、一本《赢在微点》、一本《普通高中课程标准实验教科书物理必修1》和一根草莓味棒棒糖。
草莓味棒棒糖已经被他吃完并丢弃了,而星星想必也不会喜欢物理书与物理教辅。
所以他决定就算一发导弹一条白线就能把他的小星星带到他面前,他也要再炸一条黑线给他的小星星。
也许这样会让他的爱与企盼再长大一点点吧。
至少看起来长大一点点。
顺便,把方案数也送给他的小星星。
星星被分成了两部分,那么下面的星星会下坠吧。
如果他们没有遇见像他一样的人,也许他们会遇见饥饿的小怪兽,小怪兽也许会嚼碎这些小星球。
“我就藏在漫天的星光里呀。”
他不怕外星人把他那颗星星抢走的。
抢不走的。
对于一张图 G = {V ,E} ,其中 E1 ∩ E2 = ∅,E1 ∪ E2 = E ,且图 G = {V ,E1} 为一棵树,你需要选出 两条边 e1 ∈ E1, e2 ∈ E2 ,使得图 G = {V ,∁E{e1, e2}} 不连通,求能选出的集合 {e1, e2} 数量。
输入格式
第一行包含两个整数N和M;
之后N-1行,每行包括两个整数X和Y,表示X和Y之间有一条白线; 之后M行,每行包括两个整数X和Y,表示X和Y之间有一条黑线。
输出格式
输出一个整数表示方案数。
输入输出样例
输入 #1
4 1
1 2
2 3
1 4
3 4
输出 #1
3
说明/提示
数据范围
对于20%的数据,1≤N,M≤100;
对于100%的数据,1≤N,M≤2×10^5。
样例解释
每一组边都是可行的,故答案为3*1=3
一句话题意
讲了这么多,其实意思就是:给定一棵树G={V , E1},和m条额外的边,设其集合为E2,选两条边e1∈E1,e2∈E2,删去后图不连通,求方案数
思路
树上差分(没学的先学)
传送门
另外,树上差分是要用到前缀和的,没学的一样先学
先推一篇博客:https://www.cnblogs.com/gzh-red/p/11185914.html,已经讲得非常好了,里面的例题和这道题一样,只是题面不同而已
对于每一条额外边,可能会覆盖若干条树边如图,将就着看:

1,2,4为树上的边,5为附加边,我们称1,3边被5覆盖了,因为有5的存在,删去1,3对图的连通性不影响.我们用dat[ ]记录边被覆盖的次数,但是,如果我们直接暴力将附加边相连的两个点路径上所有边的dat值+1,必然TLE,所以
树上差分华丽登场
用差分思想,对于附加边相连的两个点u,v只需dat[u]++,dat[v]++,dat[lca(u,v)]-=2,最后求前缀和即可(注意这里的差分和前缀和都是自底向上的,详情请见树上差分的博客)
那答案呢?
若一条边覆盖0次,那么将它删去图已经不连通,m条附加边随便挑;若覆盖1次,若要图不连通,只能删去覆盖它的那条边,方案数+1;若被覆盖两次或以上,那么删去该边没有贡献
代码
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#define ll long long//记得开longlong
#define nn 200010
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')c =getchar();
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re;
}
struct node{
int to , nxt;
}ed[nn * 2];
int head[nn];
void addedge(int u , int v) {
static int top = 1;
ed[top].to = v , ed[top].nxt = head[u] , head[u] = top;
++top;
}
int fa[nn];
bool vis[nn];
int dep[nn * 2];
int fir[nn];
int cnt = 0;
int ver[nn * 2];
int n , m;
int st[nn * 2][25];
ll dat[nn];
void dfs(int x , int nowdep) {
vis[x] = true;
cnt++;
fir[x] = cnt;
ver[cnt] = x;
dep[cnt] = nowdep;
for(int i = head[x] ; i ; i = ed[i].nxt) {
if(vis[ed[i].to]) {
fa[x] = ed[i].to;
continue;
}
dfs(ed[i].to , nowdep + 1);
cnt++;
ver[cnt] = x;
dep[cnt] = nowdep;
}
vis[x] = false;
}
void Init() {
dfs(1 , 1);
//RMQ
memset(st , 0 , sizeof(st));
dep[0] = (1 << 29);
for(int i = 1 ; i <= cnt ; i++)
st[i][0] = i;
int maxn = log(cnt) / log(2);
for(int j = 1 ; j <= maxn ; j++)
for(int i = 1 ; i + (1 << (j - 1)) <= cnt ; i++)
st[i][j] = dep[st[i][j - 1]] < dep[st[i + (1 << (j - 1))][j - 1]] ? st[i][j - 1] : st[i + (1 << (j - 1))][j - 1];
}
int lca(int u , int v) {//我这里采用欧拉路径+RMQ求LCA,其它方法应该也可
int x = fir[u] , y = fir[v];
if(x > y){
int tmp = x;
x = y;
y = tmp;
}
if(x == y)
return ver[st[x][0]];
int k = log(y - x) / log(2);
return ver[(dep[st[x][k]] < dep[st[y - (1 << k) + 1][k]]) ? st[x][k] : st[y - (1 << k) + 1][k] ];
}
ll ans = 0;
void GetSum(int x){
for(int i = head[x] ; i ; i = ed[i].nxt) {
if(ed[i].to == fa[x])continue;
GetSum(ed[i].to);
dat[x] += dat[ed[i].to];
switch(dat[ed[i].to]) {//随便写个switch玩玩,好久没用过了,也不知道对不对
case 0:
ans += (ll)m;
break;
case 1:
ans += 1ll;
break;
break;
}
}
}
int main() {
n = read(); m = read();
for(int i = 1 ; i < n ; i++) {
int u , v;
u = read();
v = read();
addedge(u , v);
addedge(v , u);
}
Init();
for(int i = 1 ; i <= m ; i++) {
int u , v;
u = read();
v = read();
++dat[u];
++dat[v];
dat[lca(u , v)] -= 2;
}
ans = 0;
GetSum(1);
cout << ans;
/* for(int i = 1 ; i <= cnt ; i++)
cout << ver[i] << ' ';
cout << endl;
for(int i = 1 ; i <= cnt ; i++)
cout << dep[i] << ' ';
cout << endl;
for(int j = 0 ; (1 << j) <= cnt ; j++){
cout << j << ":\t";
for(int i = 1 ; i <= cnt ; i++)
cout << st[i][j] << '\t';
cout << endl;
}*/
return 0;
}
简单的打击
题目
题目描述
帮助统治者解决问题之后,统治者准备奖励你两把剑,让你去打怪。
具体的来说,两把剑分别代表了两个长度为n的序列a,b。
你什么方面都强,所以你可以分别重新锻造这两把剑,锻造就相当于重新排列这两个序列。
合并这两把剑,让它变成一把新剑(对应序列c),合并相当于把对应位置上的数加起来c[i]=a[i]+b[i]。
最后你准备拿着这把新剑去找大Boss,造成的伤害是众数出现的次数。
问怎么排列才能使得伤害最大化,输出最大伤害。
输入格式
第一行输入一个正整数n
第二行输入n个数,表示每个a[i];
第三行输入n个数,表示每个b[i];
输出格式
输出一个整数表示最大伤害
输入输出样例
输入 #1
5
1 2 3 4 5
1 2 3 4 5
输出 #1
5
输入 #2
10
1 4 3 2 4 6 7 5 2 8
5 2 3 4 8 5 1 6 4 10
输出 #2
8
说明/提示
数据范围
对于20%的数据 n ≤ 5000
对于50%的数据 1 ≤ a[i],b[i] ≤ 5000
对于100%的数据 1 ≤ a[i],b[i] ≤ 100000,n ≤ 100000
样例解释
对于样例1,可将b序列重排为5,4,3,2,1; 此时得到c序列为6,6,6,6,6,众数6出现次数为5.
思路
玄学做法

a,b两个数组各开一个桶,如abin[i]统计i在a数组中出现了多少次,再开一个桶ans[i]表示a,b中有多少组数加起来可以得到i,答案取ans中的最大值
时间复杂度:O(100000^2)不能过
讲讲玄学优化:
O2:必开,循环展开(循环展开要配上O2才能达到最好效果)
打开O2的情况下(#3为循环展开,#3-2为普通循环):
finished: random
finished: #3 in 631 ms
finished: #3-2 in 830 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 614 ms
finished: #3-2 in 828 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 614 ms
finished: #3-2 in 1240 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 614 ms
finished: #3-2 in 825 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异
没开O2(数据量相同):
finished: random
finished: #3 in 2305 ms
finished: #3-2 in 1909 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 2290 ms
finished: #3-2 in 2437 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 2274 ms
finished: #3-2 in 1900 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异finished: random
finished: #3 in 2274 ms
finished: #3-2 in 1906 ms
正在比较文件 output.txt 和 OUTPUT2.TXT
FC: 找不到差异
以上方法平时玩玩就好,比赛不宜
正解

代码
我的(#3.cpp)
#include <iostream>
#include <cstdio>
#define nn 100010
#define rr register
//#pragma GCC optimize(2)//O2开关
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')c =getchar();
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re;
}
int abin[nn];
int bbin[nn];
int ansbin[nn * 2];
int n;
int main(){
rr int tmp = 0;
rr int am = 0;
rr int bm = 0;
n = read();
for(rr int i = 1 ; i <= n ; ++i){
tmp = read();
if(tmp > am)am = tmp;
++abin[tmp];
}
for(rr int i = 1 ; i <= n ; ++i) {
tmp = read();
if(tmp > bm)bm = tmp;
++bbin[tmp];
}
rr int bm_ = bm - 10;
for(rr int i(0) ; i <= am ; ++i){
if(abin[i] == 0)
continue;
rr int j(0);
for(j ; j <= bm_ ; j += 10){
ansbin[i + j] += (abin[i] < bbin[j] ? abin[i] : bbin[j]);
ansbin[i + j+1] += (abin[i] < bbin[j+1] ? abin[i] : bbin[j+1]);
ansbin[i + j+2] += (abin[i] < bbin[j+2] ? abin[i] : bbin[j+2]);
ansbin[i + j+3] += (abin[i] < bbin[j+3] ? abin[i] : bbin[j+3]);
ansbin[i + j+4] += (abin[i] < bbin[j+4] ? abin[i] : bbin[j+4]);
ansbin[i + j+5] += (abin[i] < bbin[j+5] ? abin[i] : bbin[j+5]);
ansbin[i + j+6] += (abin[i] < bbin[j+6] ? abin[i] : bbin[j+6]);
ansbin[i + j+7] += (abin[i] < bbin[j+7] ? abin[i] : bbin[j+7]);
ansbin[i + j+8] += (abin[i] < bbin[j+8] ? abin[i] : bbin[j+8]);
ansbin[i + j+9] += (abin[i] < bbin[j+9] ? abin[i] : bbin[j+9]);
}
for( ; j <= bm ; ++j)
ansbin[i + j] += (abin[i] < bbin[j] ? abin[i] : bbin[j]);
}
rr int maxn = 0;
for(rr int i = 0 ; i <= am + bm ; ++i)
if(maxn < ansbin[i])
maxn = ansbin[i];
cout << maxn;
return 0;
}
我的(#3-2.cpp)
#include <iostream>
#include <cstdio>
#define nn 100010
#define rr register
//#pragma GCC optimize(2)
using namespace std;
int read() {
int re = 0;
char c = getchar();
while(c < '0' || c > '9')c =getchar();
while(c >= '0' && c <= '9'){
re = (re << 1) + (re << 3) + c - '0';
c = getchar();
}
return re;
}
int abin[nn];
int bbin[nn];
int ansbin[nn * 2];
int n;
int main(){
rr int tmp = 0;
rr int am = 0;
rr int bm = 0;
n = read();
for(rr int i = 1 ; i <= n ; ++i){
tmp = read();
if(tmp > am)am = tmp;
++abin[tmp];
}
for(rr int i = 1 ; i <= n ; ++i) {
tmp = read();
if(tmp > bm)bm = tmp;
++bbin[tmp];
}
for(rr int i(0) ; i <= am ; ++i){
if(abin[i] == 0)
continue;
rr int j(0);
for(j ; j <= bm ; ++j)
ansbin[i + j] += (abin[i] < bbin[j] ? abin[i] : bbin[j]);
}
rr int maxn = 0;
for(rr int i = 0 ; i <= am + bm ; ++i)
if(maxn < ansbin[i])
maxn = ansbin[i];
cout << maxn;
return 0;
}
标准程序
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
int n,k;
int a[100010],b[100010];
long long A[300010],B[300010];
long long f[300010],g[300010];
int ans[200010],where[300010];
int pa[100010],pb[100010];
int l=0,limit=1;
long long inv;
const long long mod=998244353;
struct node{
int type,x;
bool operator<(const node a)const{
return x<a.x;
}
};
priority_queue<node> q;
void read(int&x){
x=0;
char ch=getchar();
while(ch<'0' || ch>'9') ch=getchar();
while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
}
long long ksm(long long x,long long t){
long long tot=1;
while(t){
if(t&1) (tot*=x)%=mod;
(x*=x)%=mod;
t/=2;
}
return tot;
}
long long NTT(long long*now,int id){
for(int i=0;i<limit;i++) if(i<where[i]) swap(now[i],now[where[i]]);
long long wn,w,a,b;
for(int l=2;l<=limit;l<<=1){
long long wn=f[l];
if(id==-1) wn=g[l];
for(int i=0;i<limit;i+=l){
w=1;
for(int x=i,y=i+l/2;y<i+l;x++,y++,(w*=wn)%=mod){
a=now[x],b=now[y]*w%mod;
now[x]=(a+b)%mod;now[y]=(a-b+mod)%mod;
}
}
}
}
void solve(int x){
memset(A,0,sizeof(A));memset(B,0,sizeof(B));
for(int i=1;i<=n;i++) A[i]=(a[i]>=x);
for(int i=1;i<=n;i++) B[i]=(b[i]>=x);
NTT(A,1);NTT(B,1);
for(int i=0;i<limit;i++) (A[i]*=B[i])%=mod;
NTT(A,-1);
for(int i=1;i<=2*n;i++) ans[i]+=A[i]*inv%mod;
}
int main(){
scanf("%d",&n);k=0;
int x;
while(limit<=2*n) limit*=2,l++;inv=ksm(limit,mod-2);
for(int i=0;i<limit;i++) where[i]=(where[i>>1]>>1) | ((i&1)<<(l-1));
for(int i=2;i<=limit;i<<=1) f[i]=ksm(3,(mod-1)/i),g[i]=ksm(f[i],mod-2);
for(int i=1;i<=n;i++) read(x),a[x]++;
for(int i=1;i<=n;i++) read(x),b[x]++;
int tot[2];tot[0]=tot[1]=0;
for(int i=1;i<=100000;i++) if(a[i]) q.push((node){0,a[i]});
for(int i=1;i<=100000;i++) if(b[i]) q.push((node){1,b[i]});
while(!q.empty()){
tot[q.top().type]++;
q.pop();
if(tot[0]*tot[1]>1e8) break;
}
if(!q.empty()) k=q.top().x+1;
for(int i=1;i<=k;i++) solve(i);
for(int i=1;i<=n;i++) if(a[i]>=k && a[i]) pa[++pa[0]]=i;
for(int i=1;i<=n;i++) if(b[i]>=k && b[i]) pb[++pb[0]]=i;
for(int i=1;i<=pa[0];i++)
for(int j=1;j<=pb[0];j++)
ans[pa[i]+pb[j]]+=min(a[pa[i]],b[pb[j]])-k;
int mmax=0;
for(int i=1;i<=2*n;i++) mmax=max(mmax,ans[i]);
printf("%d\n",mmax);
}
对拍(测速)
数据生成
#include <bits/stdc++.h>
using namespace std;
int random(int r , int l = 1) {
if(l == r)return l;
return (long long)rand() * rand() % (r - l) + l;
}
int main() {
int n = 10000;
printf("%d\n" , n);
for(int i = 1 ; i <= n ; i++){
printf("%d " , random(100000));
}
putchar('\n');
for(int i = 1 ; i <= n ; i++){
printf("%d " , random(100000));
}
}
对拍(测速)
#include <bits/stdc++.h>
using namespace std;
int main() {
while(true) {
system("#3random.exe > input.txt");
puts("finished:\trandom");
int tim = clock();
system("#3.exe < input.txt > output.txt");
printf("finished:\t#3 \t in %d ms\n" , clock() - tim);
tim = clock();
system("#3-2.exe < input.txt > output2.txt");
printf("finished:\t#3-2 \t in %d ms\n" , clock() - tim);
if(system("fc output.txt output2.txt")) {
cout << "WA\n";
system("start input.txt");
return 0;
}
}
return 0;
}
WC
题目
题目描述
西比拉系统正在观察一个人的心理。
这个人的心理可以抽象为一条数轴,上面存在一些非负整点,被称为「意识」。
观察的方式是选取一个非负整点作为采样点,尝试捕捉这个点附近的意识。
对于一次采样,西比拉系统会吸引在区间 [l, r] 内的意识,这时意识会向采样点靠近,此处的 [l, r] 称为这次采样的 吸引区间。
每次采样又会有一个参数,捕捉半径 t ,表示如果有意识可以被吸引而移动到 [x1 − t,x1 + t] 范围内,其数据就 会被捕捉。其中 x1 表示采样点的位置。
注意,当一次采样结束,所有意识都会回到原来的位置。
每个意识会有一个参数,思维强度 s ,表示这个意识被吸引时的可移动范围为 [x2 − s,x2 + s] ,其中 x2 表示 这个意识出现的位置。
初始时数轴上没有意识,此后每个时刻仅会发生一个事件。 事件有两种:
·意识事件,形如 T x2 s ,表示在 x2 处出现了一个思维强度为 s 的意识。 ·采样事件,形如 G x1 l r t ,表示在 x1 处进行一次吸引区间为 [l, r] ,捕捉半径为 t ,请求出会被捕捉到的 意识的个数。
对于每次采样,请求出会被捕捉到的意识的个数。
输入格式
第一行,一个整数 n,表示西比拉系统的判断总共进行了 n 个时刻。
以下 n 行,第 i 行表示第 i 个时刻发生的事件。
输出格式
对于每个采样事件,输出会被捕捉到的意识的个数。
输入输出样例
输入 #1
5
G 1 1 1 0
T 0 3
T 10 1
T 10 3
G 5 0 10 2
输出 #1
0
2
说明/提示
数据范围
对于 30% 的数据,n <= 10^4;
对于 60% 的数据,n <= 2 × 10^4;
对于 80% 的数据,n <= 5 × 10^4;
对于 100% 的数据,1 <= n <= 10^5, 0 <= x1,x2,s,t <= 10^9, 0 <= l <= r <= 10^9。
其中 20% 的数据,所有采样事件都在意识事件之后。
其中 40% 的数据,所有意识事件的 x2 均不大于所有采样事件的 x1。
样例解释
对于第一次采样事件,显然一个意识都没有。
对于第二次采样事件,坐标为 0 的意识最多移动到 3 处,坐标为 10 的意识分别最多移动到 9,7 处,其中在 [3,7] 区间内的有两个意识。
思路
暴力出奇迹,打表出省一
正解?CDQ分治?不可做,30分钟写个70分暴力它不香吗

代码
考场暴力
#include <iostream>
#include <cstdio>
#define rr register
#define nn 100010
using namespace std;
int read() {
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re * sig;
}
bool GetTy() {
char c = getchar();
while(c != 'G' && c != 'T')c = getchar();
return c == 'T';
}
struct node{
int x , s;
}a[nn];
void print(int x) {
if(x < 0){
putchar('-');
x = -x;
}
rr int a = 0 , cnt = 0;
do{
a = (a << 1) + (a << 3) + x % 10;
x /=10;
++cnt;
}while(x != 0);
for(rr int i = 1 ; i <= cnt ; i++){
putchar(a % 10 + 48);
a /= 10;
}
}
int main() {
rr int n = read();
rr int top = 0;
while(n--) {
if(GetTy()){
++top;
a[top].x = read() ,a[top].s = read();
}
else {
rr int x , l , r , t;
x = read() , l = read() , r = read() , t = read();
rr int cnt = 0;
for(rr int i = 1 ; i <= top ; i++) {
if(a[i].x >= l && a[i].x <= r) {
if((a[i].x + a[i].s >= x - t && a[i].x - a[i].s <= x + t) || (a[i].x - a[i].s <= x + t && a[i].x + a[i].s >= x - t))
cnt++;
}
}
print(cnt);
putchar('\n');
}
}
return 0;
}
正解(来自参考程序)
#include <cstdio>
#include <cassert>
#include <cstring>
#include <algorithm>
#define lowbit(x) ((x) & -(x))
using namespace std;
const int N = 1e5;
int n,m,tot;
int ind[N + 5],len;
long long c[N + 5];
inline void update(int x,long long k)
{
for(;x <= len;x += lowbit(x))
c[x] += k;
}
inline long long query(int x)
{
long long ret = 0;
for(;x;x -= lowbit(x))
ret += c[x];
return ret;
}
struct note
{
int x,y,z,id,w,part;
} a[N * 2 + 5],t1[N * 2 + 5],t2[N * 2 + 5];
long long ans[N + 5];
void cdq(int l,int r)
{
if(l == r)
return ;
int mid = l + r >> 1;
cdq(l,mid),cdq(mid + 1,r);
int i = l,j = mid + 1,k = l;
while(i <= mid && j <= r)
if(t1[i].y <= t1[j].y)
{
if(!t1[i].part && !t1[i].id)
update(t1[i].z,1);
t2[k++] = t1[i++];
}
else
{
if(t1[j].part && t1[j].id)
ans[t1[j].id] += t1[j].w * query(t1[j].z);
t2[k++] = t1[j++];
}
while(i <= mid)
{
if(!t1[i].part && !t1[i].id)
update(t1[i].z,1);
t2[k++] = t1[i++];
}
while(j <= r)
{
if(t1[j].part && t1[j].id)
ans[t1[j].id] += t1[j].w * query(t1[j].z);
t2[k++] = t1[j++];
}
for(register int i = l;i <= mid;++i)
if(!t1[i].part && !t1[i].id)
update(t1[i].z,-1);
for(register int i = l;i <= r;++i)
t1[i] = t2[i];
}
void CDQ(int l,int r)
{
if(l == r)
return ;
int mid = l + r >> 1;
CDQ(l,mid),CDQ(mid + 1,r);
int i = l,j = mid + 1,k = l;
while(i <= mid && j <= r)
if(a[i].x <= a[j].x)
a[i].part = 0,t1[k++] = a[i++];
else
a[j].part = 1,t1[k++] = a[j++];
while(i <= mid)
a[i].part = 0,t1[k++] = a[i++];
while(j <= r)
a[j].part = 1,t1[k++] = a[j++];
for(register int i = l;i <= r;++i)
a[i] = t1[i];
cdq(l,r);
}
int main()
{
scanf("%d",&n);
char op;
int x,s,l,r;
for(register int i = 1;i <= n;++i)
{
scanf(" %c%d",&op,&x);
if(op == 'T')
{
scanf("%d",&s);
a[++tot] = (note){x,x - s,-(x + s),0,0,0};
ind[i] = -(x + s);
}
else
{
scanf("%d%d%d",&l,&r,&s);
a[++tot] = (note){l - 1,x + s,s - x,++m,-1,0};
a[++tot] = (note){r,x + s,s - x,m,1,0};
ind[i] = s - x;
}
}
sort(ind + 1,ind + n + 1);
len = unique(ind + 1,ind + n + 1) - ind - 1;
for(register int i = 1;i <= tot;++i)
a[i].z = lower_bound(ind + 1,ind + len + 1,a[i].z) - ind;
CDQ(1,tot);
for(register int i = 1;i <= m;++i)
printf("%lld\n",ans[i]);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号