20201103提高组训练(选数字&堆箱子&快速排序&统计学带师)
A 选数字
题目
题目描述
桌面上有N个数字排成一排,小武要求小林从中选出3个数字,使得这3个数字的按位或的结果恰好等于x,小林很快 就解决了这个问题,小武想了想,决定把问题加强一下,小武会问小林Q次问题,每次选的3个数字只能在从左往右 的第l个数和第r个数之间选择,并且要小林说出符合要求的方案数,小林顿时不会了,于是把问题交给了你。
输入格式
第一行两个数N和Q 第二行N个数,按照从左到右的顺序给出桌面上的数字 接下来Q行,每行3个数字,分别为l,r,x
输出格式
Q行,每行一个数表示方案数
输入输出样例
输入 #1
10 5
2 4 3 7 6 9 8 7 10 15
1 5 7
2 8 14
3 5 7
1 10 15
6 9 12
输出 #1
9
1
1
81
0
说明/提示
数据范围
对于20%的数据,n,Q≤100
对于60%的数据,n,Q≤10000
对于100%的数据,1≤l≤r≤n≤10^5 ,1≤Q≤10^5,1≤桌面上每个数字,x≤255
样例解释
第一个询问,选择范围为{2,4,3,7,6}。除了选2 4 6不行,剩下9种方案均可以
思路
首先,根据或运算的性质,一个数a[i],若它在二进制下的某一位为1,而x在对应位上为0,a[i]是绝对不可能通过或运算得到x的
考虑到x和a[]只能去到255,我们开数组sum[i] [j]表示1~i中a[k]的个数,满足(a[k] & j)==a[k],即a[k]有可能通过或运算得到 j
定义f(x)表示x在二进制下有多少个"1"(程序中cnt[x]的意义同f(x))
则对于每一组问题l,r,x
即在[l,r]中,对于所有j,x & j == j,所有(a[i]&j)==a[i] (有可能异或得到x的a[i]),若f(x)-f(j)为奇数,从ans中减去 满足条件的a[i]的数量 的组合数,否则加上。
为什么呢?
在所有可能组成x的数中取三个,有可能取到的数不合法(或运算后不等于x),就要减去,所以我们要枚举j,如果j的二进制下只有一位和x不同(j的那一位为0,而x为1),那么区间内经过或运算可能得到j的数之间 进行或运算是一定得不到x的,这些数的组合应当减去,故容斥系数为-1。但是有可能会减掉一些重复的组合,如(0000,1000,1001)在j=(1011)和j=(1101)时均会被减掉,故在j=(1001)时应该被加回,以此类推,得到f(x)-f(j)为偶数时容斥系数为1,f(x)-f(j)为奇数时容斥系数为-1.
代码
#include <iostream>
#include <cstdio>
#define nn 100010
#define ll long long
using namespace std;
int read() {
int re = 0 , sig = 1;
char c = getchar();
while(c < '0' || c > '9'){
if(c == '-')sig = -1;
c = getchar();
}
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c =getchar();
return re * sig;
}
ll C(ll x){
return x * (x - 1) * (x - 2) / 6;
}
int n , q;
int a[nn];
int cnt[350];
int sum[nn][350];
inline int f(int x){
int cnt = 0;
while(x > 0){
x = x & (x - 1);
cnt++;
}
return cnt;
}
int main(){
cnt[0] = 0 , cnt[1] = 1 , cnt[2] = 1;
for(int i = 3 ; i <= 300 ; i++)
cnt[i] = cnt[i / 2] + (i & 1);
// for(int i = 1 ; i <= 10 ; i++)
// cout << i << '\t' << cnt[i] << endl;
n = read() , q = read();
for(int i = 1 ; i <= n ; i++)
a[i] = read();
for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= 255 ; j++)
sum[i][j] = sum[i - 1][j] + ((a[i] & j) == a[i] ? 1 : 0);
for(int i = 1 ; i <= q ; i++){
int l , r , x;
long long ans = 0;
l = read() , r = read() , x = read();
for(int j = 0 ; j <= 255 ; j++){
if((j & x) != j)continue;
int op = cnt[x] - cnt[j];
if(op & 1) ans -= C((ll)sum[r][j] - sum[l - 1][j]);
else ans += C((ll)sum[r][j] - sum[l - 1][j]);
}
printf("%lld\n" , ans);
}
return 0;
}
B 堆箱子
题目
题目描述
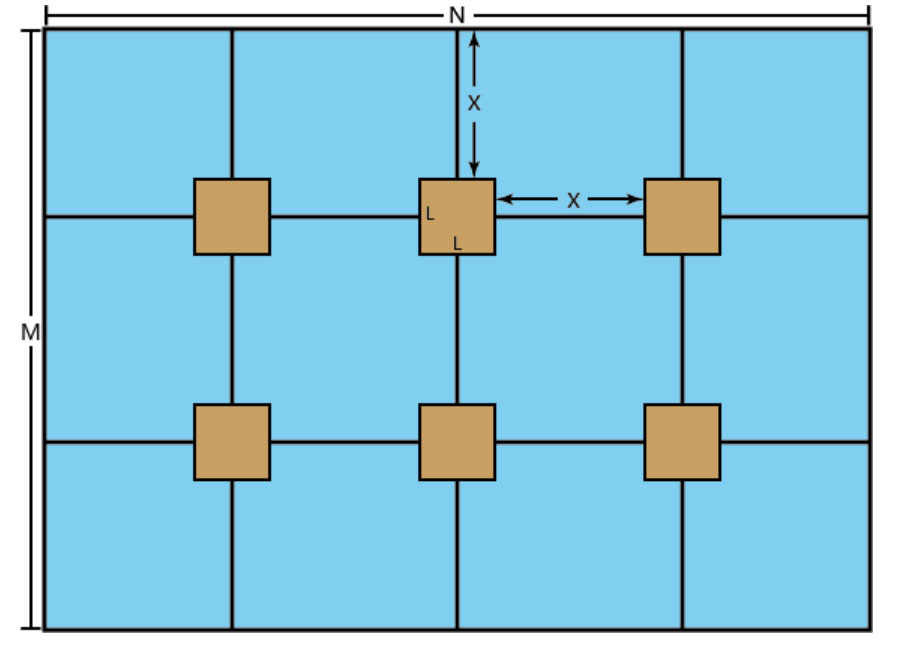
仓库中有很多的箱子,这天小武想把箱子收拾一下。仓库是一个长方体,我们不用考虑仓库的高度,仓库的长度为 N,宽度为M,箱子是一个标准的正方体,边长为L。小武很严格,对于箱子的摆放有很严格的要求。小武要求用若 干根直线等分仓库的长和宽,而箱子只能放在等分长和宽的直线的交点上,并且一个箱子到四个方向的距离(可能 是到另一个箱子, 也可能是到仓库的边缘),必须相同。那么在满足要求的前提下,小武想放心尽可能多的箱子, 那么此时一个箱子到四个方向的距离是多少呢?(设这个距离为x)
输入格式
一行三个数表示L,N,M
输出格式
一行一个实数表示距离x,精确到小数点后五位 如果无法满足要求,输出-1
输入输出样例
输入 #1
2 18 13
输出 #1
0.50000
输入 #2
4 26 26
输出 #2
0.28571
输入 #3
3 46 18
输出 #3
0.50000
说明/提示
数据范围
对于24%的数据,1≤L≤100,1≤N,M≤1000
对于48%的数据,1≤L≤1000,1≤L,N,M≤10^6
对于80%的数据,1≤L≤10^6
对于100%的数据,1≤L,N,M≤10^9
样例解释
对于样例1,横排放7个箱子,竖排放5个箱子,x=(18-27)/8=(13-25)/6=0.50000
思路
其实就是一道数学题,我搞了这么久还WA了证明我太菜了
我们将箱子间的距离看成长度为x的线段
原仓库从横/纵看就是(线段-箱子-线段-箱子……-箱子-线段)的形式
为了方便,我们将仓库扩展到(M+L)*(N+L)
仓库变成(线段-箱子-线段-箱子……-箱子-线段-箱子)的形式,即若干个(线段-箱子)的组合
将一个(线段-箱子)长度设为y(y不一定为整数)
根据题意,则有
设
g一定是最大的能同时整除(M+L)和(N+L)的数
根据y的定义,y一定大于等于L
所以
题目要我们求的就是最小的(y-L)
因为
所以有
设
又因为
所以
所以
又因为z为整数
所以最优解为(y最小,z就要最大):
输出-1的情况:上面提到,y的取值范围:[L,g]当g<L时,y无解,特别地,若g>M或g>N,也输出-1
代码
#include <iostream>
#include <cstdio>
using namespace std;
int l , m , n;
int gcd(int a , int b) {
return b == 0 ? a : gcd(b , a % b);
}
int main() {
cin >> l >> n >> m;
int g = gcd(n + l , m + l);
if(g < l || n < l || m < l)
cout << "-1";
else
printf("%.5lf",1.0 * g / ( g / l) - l);
return 0;
}
C 快速排序
题目
题目描述
小武最近学习了快速排序,写出了下述的代码
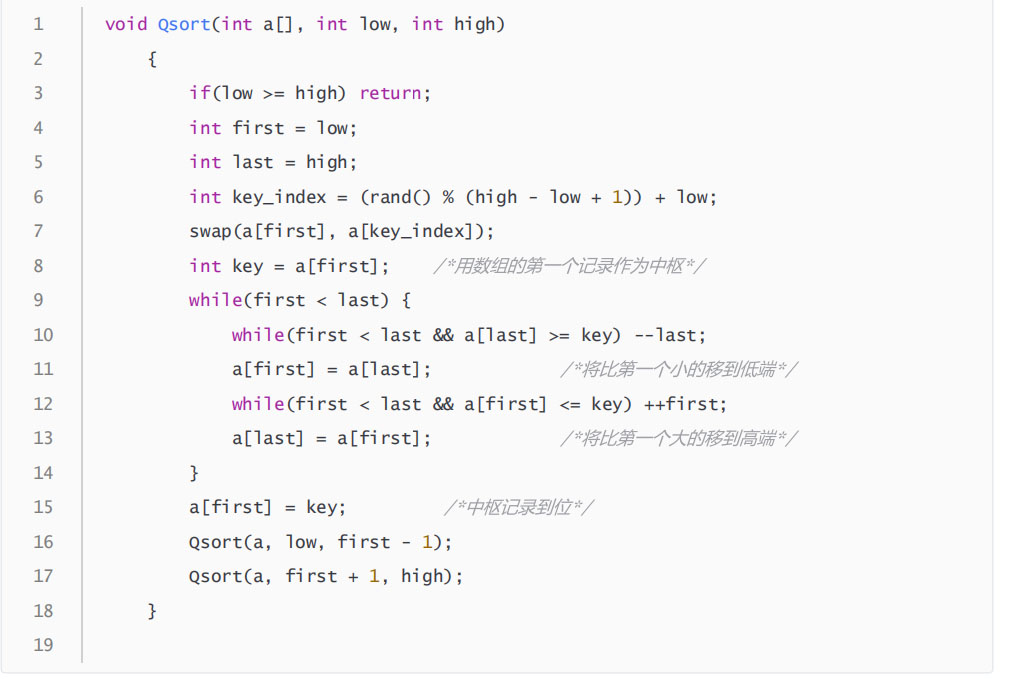
这里开始low=0,high=N,数组a为1-N的一个排列
我们采用随机优化的快速排序是很难碰到最坏情况的,但是小林偷偷修改了运行环境,控制了随机数的生成,使得 随机数依次为a1,a2,a3,...,ak,a1,...,即随机数结果依次为a1到ak,然后不断循环。但是还有一个问题,什么样的排列 在这样的随机数下效果最差呢,小林认为效果最差即递归的深度最深,但小林不知道怎么找到这个排列,只好交给 了你
输入格式
第一行两个整数N和k
接下来k行,每行一个数字,表示a1到ak
输出格式
N行整数,为1-N的一个排列,若有多个排列满足条件,输出其中字典序最小的那个排列
输入输出样例
输入 #1
3 1
0
输出 #1
1
2
3
输入 #2
4 2
1
0
输出 #2
1
4
2
3
输入 #3
1 1
0
输出 #3
1
说明/提示
数据范围
对于40%的数据,1=N,k<=10
对于70%的数据,1<=N,k<=10000
对于100%的数据,1<=N,k<=50000, 0<=ai<=10^9
样例解释
对于样例1
(1,2,3) 递归深度为3层,字典序最小
对于样例2
(1, 4, 2, 3)递归深度为4层,字典序最小
(1,2,3,4) -> (1) 2 (3,4) -> 1 2 3 (4) 字典序小,但是只有3层深度
思路
要想卡掉快排就要知道快排的原理:
- 在当前区间选定一个标准值(题中的程序用随机选定)
- 把比标准值小的放在左边,大的放在右边
- 以标准值的下标(经过上述操作)为分界点,进行递归,直到区间长度为1
如果每一次选的标准值都是最小或最大值,那么标准值就会被扔到最左边或最右边,递归的深度就可能达到n,这就是题目所要的
其实卡的方法我知道,但是因为太菜了不会实现,就没有做QAQ
具体模拟及实现题解已经很清楚了:

代码
#include <iostream>
#include <cstdio>
#include <cstring>
#define nn 50010
using namespace std;
inline void swap(int &x , int &y){
int tmp;
tmp = x ; x = y ; y = tmp;
}
int read(){
int re = 0;
char c = getchar();
while(c < '0' || c > '9')
c = getchar();
while(c >= '0' && c <= '9')
re = (re << 1) + (re << 3) + c - '0',
c = getchar();
return re;
}
int n , k;
int r[nn] , a[nn] , ans[nn];
int dict[nn];
int main(){
n = read() , k = read();
for(int i = 0 ; i < k ; i++)
r[i] = read();
for(int i = 0 ; i < n ; i++)
dict[i] = i;
int left = 0 , right = n - 1;
int minn = 0;
memset(ans , 0 , sizeof(ans));
for(int i = 0 ; i < n ; i++) {
int p = (r[i % k] % (right - left + 1));
p += left;
// cout << p << endl;
if(dict[p] == minn){
ans[dict[p]] = left + 1;//这里一定要加1,不然left为0的时候下面找最小会出问题
swap(dict[p] , dict[left]);
left++;
while(ans[minn] != 0)minn++;
//minn++;
}
else {
ans[dict[p]] = right + 1;
swap(dict[p] , dict[left]);
swap(dict[left] , dict[right]);
right--;
}
}
for(int i = 0 ; i < n ; i++)
printf("%d\n" , ans[i]);
return 0;
}
/*
10 5
1
2
3
4
5
1
10
9
8
7
6
2
4
5
3
*/
D 统计学带师
题目
题目描述

输入格式
第一行,两个正整数 n, q。
第二行,一个字符串 S。
以下 n 行,第 i 行一个字符串 s_i。
以下 q 行,每行三个正整数 l, r, k。
输出格式
q 行,每行一个整数,表示小 L 的第 i 个问题的答案。
输入输出样例
输入 #1
5 4
abcbcq
abc
bcd
acbc
qcbcba
qwqwq
1 2 2
3 5 4
2 3 3
6 6 1
输出 #1
0
1
1
0
说明/提示
数据范围
对于 40% 的数据,n, q, |S|, ∑|s_i| <= 10^3;
对于 100% 的数据,1 <= n, |S|, ∑|s_i| <= 10^5, 1 <= q <= 2 × 10^5, 1 <= l <= r <= |S|, 1 <= k <= n,所有 字符串均仅包含小写字母
样例解释

思路
自动机?没学

代码(来自参考程序)
#include <cstdio>
#include <vector>
#include <utility>
#include <cstring>
using namespace std;
const int N = 1e5;
const int Q = 2e5;
const int LG = 18;
int n,m,q;
int ed[N + 5],len[N + 5];
char s[N + 5],t[N + 5];
int ans[Q + 5];
namespace SEG
{
#define ls (p << 1)
#define rs (ls | 1)
int seg[(N << 3) + 10];
void insert(int x,int k,int p,int tl,int tr)
{
seg[p] += k;
if(tl == tr)
return ;
int mid = tl + tr >> 1;
x <= mid ? insert(x,k,ls,tl,mid) : insert(x,k,rs,mid + 1,tr);
}
int query(int k,int p,int tl,int tr)
{
if(tl == tr)
return tl;
int mid = tl + tr >> 1;
int sum = seg[ls];
return k <= sum ? query(k,ls,tl,mid) : query(k - sum,rs,mid + 1,tr);
}
}
namespace SAM
{
struct node
{
int ch[26];
int fa,len;
} sam[(N << 1) + 5];
int las = 1,tot = 1;
int c[N + 5],a[(N << 1) + 5];
int sz[(N << 1) + 5],son[(N << 1) + 5];
vector<int> edp[(N << 1) + 5];
inline void insert(int x,int pos)
{
if(sam[las].ch[x])
{
int cur = las,q = sam[cur].ch[x];
if(sam[cur].len + 1 == sam[q].len)
las = q,++sz[las],edp[las].push_back(pos);
else
{
int nxt = ++tot;
sam[nxt] = sam[q],sam[nxt].len = sam[cur].len + 1,sam[q].fa = nxt;
for(;cur && sam[cur].ch[x] == q;cur = sam[cur].fa)
sam[cur].ch[x] = nxt;
las = nxt,++sz[las],edp[las].push_back(pos);
}
return ;
}
int cur = las,p = ++tot;
sam[p].len = sam[cur].len + 1;
for(;cur && !sam[cur].ch[x];cur = sam[cur].fa)
sam[cur].ch[x] = p;
if(!cur)
sam[p].fa = 1;
else
{
int q = sam[cur].ch[x];
if(sam[cur].len + 1 == sam[q].len)
sam[p].fa = q;
else
{
int nxt = ++tot;
sam[nxt] = sam[q],sam[nxt].len = sam[cur].len + 1,sam[p].fa = sam[q].fa = nxt;
for(;cur && sam[cur].ch[x] == q;cur = sam[cur].fa)
sam[cur].ch[x] = nxt;
}
}
las = p,++sz[las],edp[las].push_back(pos);
}
int to[(N << 1) + 5],pre[(N << 1) + 5],first[(N << 1) + 5];
inline void add(int u,int v)
{
static int tot = 0;
to[++tot] = v,pre[tot] = first[u],first[u] = tot;
}
int f[LG + 5][(N << 1) + 5];
inline void build()
{
for(register int i = 1;i <= tot;++i)
++c[sam[i].len],i > 1 && (add(f[0][i] = sam[i].fa,i),1);
for(register int i = 1;i <= LG;++i)
for(register int j = 2;j <= tot;++j)
f[i][j] = f[i - 1][f[i - 1][j]];
for(register int i = 1;i <= N;++i)
c[i] += c[i - 1];
for(register int i = tot;i > 1;--i)
a[c[sam[i].len]--] = i;
for(register int i = tot;i > 1;--i)
{
sz[sam[a[i]].fa] += sz[a[i]];
if(!son[sam[a[i]].fa] || sz[son[sam[a[i]].fa]] < sz[a[i]])
son[sam[a[i]].fa] = a[i];
}
}
inline int get(int p,int d)
{
if(sam[p].len < d)
return 0;
for(register int i = LG;~i;--i)
if(f[i][p] && sam[f[i][p]].len >= d)
p = f[i][p];
return p;
}
vector< pair<int,int> > qry[(N << 1) + 5];
int cnt[N + 5];
void dfs(int p)
{
for(register int i = first[p];i;i = pre[i])
if(to[i] ^ son[p])
{
dfs(to[i]);
for(register vector<int>::iterator it = edp[to[i]].begin();it != edp[to[i]].end();++it)
SEG::insert(cnt[*it],-1,1,0,N),--cnt[*it],SEG::insert(cnt[*it],1,1,0,N);
}
if(son[p])
dfs(son[p]);
for(register vector<int>::iterator it = edp[p].begin();it != edp[p].end();++it)
SEG::insert(cnt[*it],-1,1,0,N),++cnt[*it],SEG::insert(cnt[*it],1,1,0,N);
if(son[p])
{
edp[p].swap(edp[son[p]]);
for(register vector<int>::iterator it = edp[son[p]].begin();it != edp[son[p]].end();++it)
edp[p].push_back(*it);
vector<int>().swap(edp[son[p]]);
}
for(register int i = first[p];i;i = pre[i])
if(to[i] ^ son[p])
for(register vector<int>::iterator it = edp[to[i]].begin();it != edp[to[i]].end();++it)
edp[p].push_back(*it),
SEG::insert(cnt[*it],-1,1,0,N),++cnt[*it],SEG::insert(cnt[*it],1,1,0,N);
for(register vector< pair<int,int> >::iterator it = qry[p].begin();it != qry[p].end();++it)
ans[it->second] = SEG::query(it->first,1,0,N);
}
}
int main()
{
scanf("%d%d%s",&n,&q,s + 1),m = strlen(s + 1);
for(register int i = 1;i <= n;++i)
{
scanf("%s",t),SAM::las = 1;
for(register char *c = t;*c;SAM::insert(*c++ - 'a',i));
}
SAM::build();
for(register int i = 1,x,p = 1,l = 0;i <= m;++i)
{
x = s[i] - 'a';
if(SAM::sam[p].ch[x])
p = SAM::sam[p].ch[x],++l;
else
{
for(;p && !SAM::sam[p].ch[x];p = SAM::sam[p].fa);
!p ? (p = 1,l = 0) : (l = SAM::sam[p].len + 1,p = SAM::sam[p].ch[x]);
}
ed[i] = p,len[i] = l;
}
int l,r,k;
for(register int i = 1;i <= q;++i)
scanf("%d%d%d",&l,&r,&k),
len[r] >= r - l + 1 && (SAM::qry[SAM::get(ed[r],r - l + 1)].push_back(make_pair(k,i)),1);
SEG::insert(0,n,1,0,N),SAM::dfs(1);
for(register int i = 1;i <= q;++i)
printf("%d\n",ans[i]);
}




