BZOJ5297 CQOI2018 社交网络 【矩阵树定理Matrix-Tree】

BZOJ5297 CQOI2018 社交网络

---

Description

当今社会，在社交网络上看朋友的消息已经成为许多人生活的一部分。通常，一个用户在社交网络上发布一条消息（例如微博、状态、Tweet等）后，他的好友们也可以看见这条消息，并可能转发。转发的消息还可以继续被人转发，进而扩散到整个社交网络中。在一个实验性的小规模社交网络中我们发现，有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程，我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便，我们将初始消息发送者编号为1，其他用户编号依次递增。该社交网络上的所有好友关系是已知的，也就是说对于A、B两个用户，我们知道A用户可以看到B用户发送的消息。注意可能存在单向的好友关系，即A能看到B的消息，但B不能看到A的消息。还有一个假设是，如果某用户看到他的多个好友转发了同一条消息，他只会选择从其中一个转发，最多转发一次消息。从不同好友的转发，被视为不同的情况。如果用箭头表示好友关系，下图展示了某个社交网络中消息转发的所有可能情况。

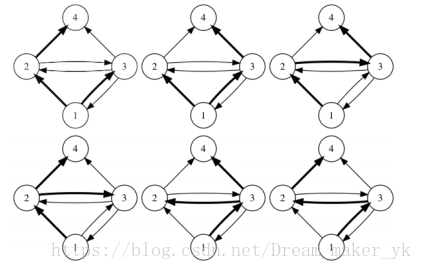
初始消息是用户1发送的，加粗箭头表示一次消息转发

Input

输入文件第一行，为一个正整数n，表示社交网络中的用户数：
第二行为一个正整数m．表示社交网络中的好友关系数目。
接下来m行，每行为两个空格分隔的整数ai和bi，表示一组好友关系，即用户ai可以看到用户bi发送的消息。
1≤n≤250,1≤ai，bi≤n，1≤m≤n(n-1)

Output

输出文件共一行，为一条消息所有可能的转发途径的数量，除以1 0007所得的余数。

Sample Input

4
7
2 1
3 1
1 3
2 3
3 2
4 3
4 2

Sample Output

6

---

矩阵树定理（Matrix-Tree）现学现用。
对于无向图：
* 主对角线记录每个点度数
* 如果i→j$i\to j$有边就在fi,j$f_{i,j}$处减一(保证每一列和为零)
对于有向图：
* 主对角线记录每个点出度
* 如果i→j$i\to j$有边就在fj,i$f_{j,i}$处减一(保证每一列和为零)
如果固定根就删除根所在行列然后求矩阵的行列式
否则随便删一行一列求行列式

---

然后就发现这道题其实是模板

---

#include<bits/stdc++.h>
using namespace std;
const int N=260,Mod=10007;
int n,m,sign=1,f[N][N];
void solve(){
    for(int i=1;i<n;i++)
        for(int j=i+1;j<n;j++){
            while(true){
                if(!f[j][i])break;
                int x=f[i][i]/f[j][i];
                for(int k=1;k<n;k++)
                    f[i][k]=(f[i][k]-f[j][k]*x%Mod+Mod)%Mod;
                for(int k=1;k<n;k++)swap(f[i][k],f[j][k]);
                sign*=-1;
            }
        }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        int u,v;scanf("%d%d",&v,&u);
        v--;u--;
        if(u!=v)f[u][v]--;
        if(v)f[v][v]++;
    }
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            f[i][j]=(f[i][j]%Mod+Mod)%Mod;
    solve();
    int ans=1;
    for(int i=1;i<n;i++)ans=ans*f[i][i]%Mod;
    ans=(ans*sign%Mod+Mod)%Mod;
    printf("%d\n",ans);
    return 0;
}