Luogu1155 NOIP2008 双栈排序 【二分图染色】【模拟】

Luogu1155 NOIP2008 双栈排序

---

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过 2个栈 S1 和 S2 ，Tom希望借助以下 44 种操作实现将输入序列升序排序。

操作 a 如果输入序列不为空，将第一个元素压入栈 S1
操作 b 如果栈 S1 不为空，将 S1 栈顶元素弹出至输出序列
操作 c 如果输入序列不为空，将第一个元素压入栈 S2
操作 d 如果栈 S2 不为空，将 S2 栈顶元素弹出至输出序列
如果一个 1-n的排列P可以通过一系列操作使得输出序列为 1,2,…,(n-1),n，Tom就称 PP 是一个“可双栈排序排列”。例如 (1,3,2,4)就是一个“可双栈排序序列”，而 (2,3,4,1)不是。下图描述了一个将 (1,3,2,4)排序的操作序列：
<a,c,c,b,a,d,d,b>$<a,c,c,b,a,d,d,b>$

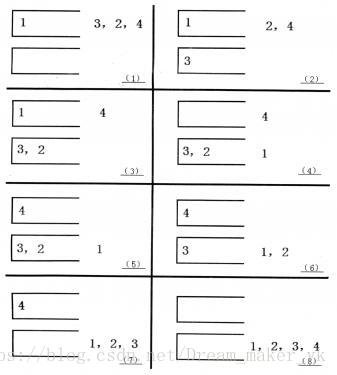
当然，这样的操作序列有可能有几个，对于上例 (1,3,2,4)，

输入输出格式

输入格式：
第一行是一个整数 n 。
第二行有 n个用空格隔开的正整数，构成一个 1-n的排列
输出格式：
共一行，如果输入的排列不是“可双栈排序排列”，输出数字 0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入样例#1：

4
1 3 2 4

输出样例#1：

a b a a b b a b

输入样例#2：

4
2 3 4 1

输出样例#2：

0

输入样例#3：

3
2 3 1

输出样例#3：

a c a b b d

说明

30% 的数据满足： n≤10
50% 的数据满足： n≤50
100% 的数据满足： n≤1000

---

一开始没看出来是二分图染色，网上好像有方法模拟+贪心过的，ORZ
我们可以发现如果对于k

//yangkai
#include<bits/stdc++.h>
using namespace std;
#define N 1010
int n,a[N],mink[N],col[N],g[N][N];
bool dfs(int x){
    for(int i=1;i<=n;i++)
        if(g[i][x]){
            if(col[i]!=-1){
                if(col[x]!=col[i])continue;
                return 0;
            }
            col[i]=1-col[x];
            dfs(i);
        }
    return 1;
}
int main(){
    memset(mink,0x3f,sizeof(mink));
    memset(col,-1,sizeof(col));
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=n;i>=1;i--)mink[i]=min(mink[i+1],a[i]);
    for(int i=1;i<=n;i++)
        for(int j=i+1;j<=n;j++)
            if(a[i]<a[j]&&mink[j+1]<a[i])
                g[i][j]=g[j][i]=1;
    for(int i=1;i<=n;i++)if(col[i]==-1){
        col[i]=1;
        if(!dfs(i)){
            printf("0");
            return 0;
        }
    }
    int st=col[1],las=0;
    stack<int> p1,p2;
    for(int i=1;i<=n;i++){
        if(col[i]==st){
            while(!p1.empty()&&p1.top()<a[i]){
                if(!p2.empty()&&p2.top()<p1.top()){las=p2.top();p2.pop();printf("d ");}
                else{las=p1.top();p1.pop();printf("b ");}
            }
            p1.push(a[i]);
            printf("a ");
        }else{
            while(!p2.empty()&&p2.top()<a[i]){
                if(!p1.empty()&&p2.top()>p1.top()){las=p1.top();p1.pop();printf("b ");}
                else{las=p2.top();p2.pop();printf("c ");}
            }
            while(!p1.empty()&&p1.top()==las+1){
                las++;
                p1.pop();
                printf("b ");
            }
            p2.push(a[i]);
            printf("c ");
        }
    }
    while(!p1.empty()&&!p2.empty()){
        if(p1.top()<=p2.top()){p1.pop();printf("b ");}
        else{p2.pop();printf("d ");}
    }
    while(!p1.empty()){p1.pop();printf("b ");}
    while(!p2.empty()){p2.pop();printf("d ");}
    return 0;
}