双指针算法详解
双指针算法详解
参考链接
练习题
相关链接
什么是双指针
双指针,指的是在遍历对象的过程中,不是普通的使用单个指针[或者称之为变量]进行访问,而是使用两个相同方向(快慢指针)或者相反方向(对撞指针)的指针进行扫描,从而达到相应的目的。
换言之,双指针法充分使用了数组有序这一特征,从而在某些情况下能够简化一些运算。
在 LeetCode 题库中,关于双指针的问题还是挺多的。双指针
双指针从广义上来说,是指用两个变量在线性结构上遍历而解决的问题。狭义上说,
- 对于数组,指两个变量在数组上相向移动解决的问题;
- 对于链表,指两个变量在链表上同向移动解决的问题,也称为「快慢指针」问题。
双指针算法通常不难,双指针算法是基于暴力解法的优化,它们是很好的学习算法的入门问题,让我们开始学习双指针算法之旅吧。
快慢指针(Fast & Slow pointers)
基本原理及应用场景
快慢指针方法,又称为龟兔赛跑算法,其基本思想就是使用两个移动速度不同的指针(快指针是慢指针的X倍,X > 1)在数组或链表等序列结构上移动。这种方法对于处理「环形」链表或数组非常有用。以链表为例,通过以不同的速度移动,我们可以证明如果链表中存在环,则两个指针必定会相遇,当两个指针均处在环中时,快指针会追上慢指针(如下图所示)。
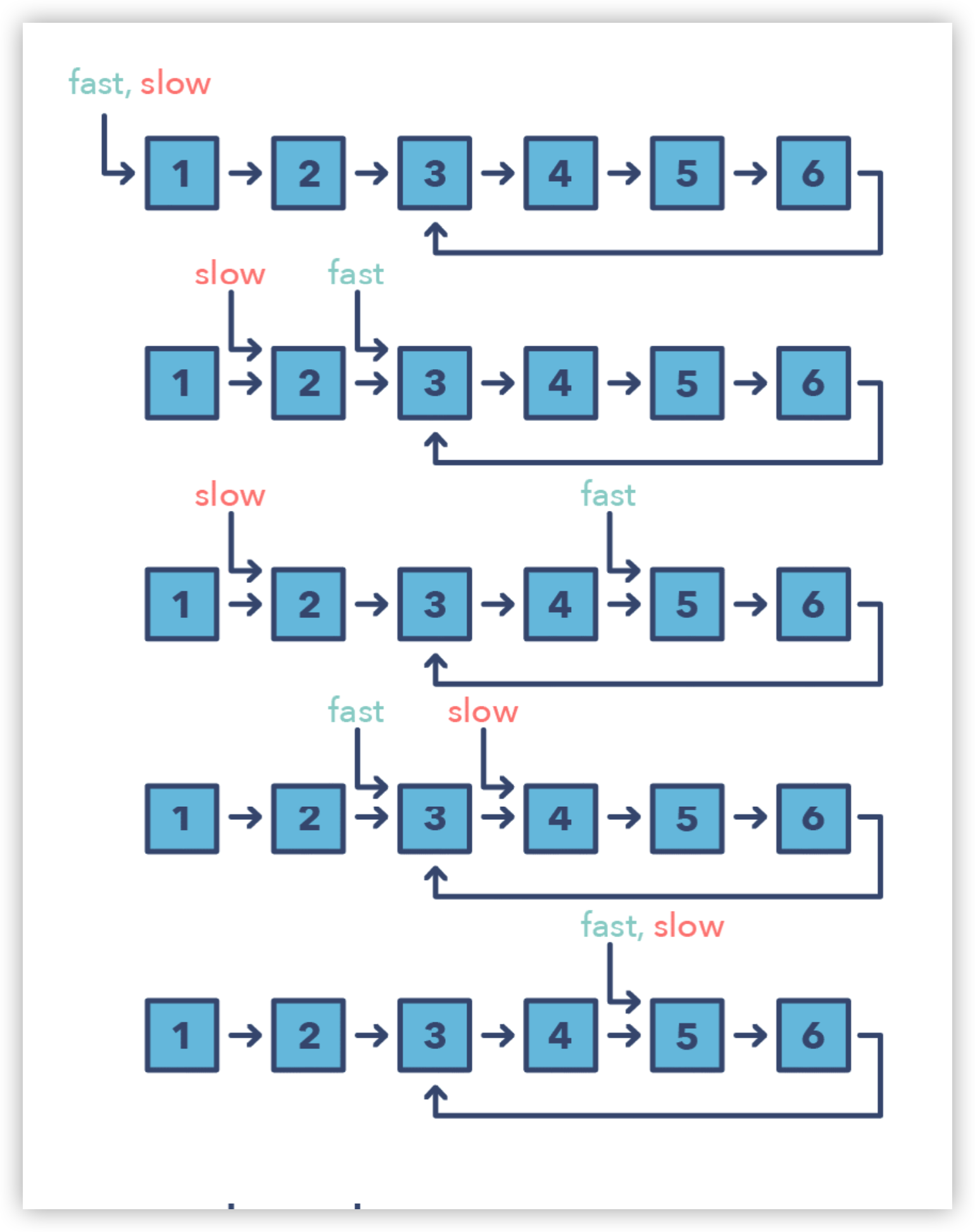
为什么说快指针一定会追上慢指针?,即快慢指针一定会相遇?
这个问题你可以用数学归纳法来思考。首先,由于链表是个环,所以相遇的过程可以看作是快指针从后边追赶慢指针的过程。那么做如下思考:
当快慢两个指针均落入环中之后【一直往下走两个指针必定均会落入环中】,落入环中时就一定会是如下情况中的一种,我们归纳讨论HINT: 这里我们不考虑当快慢指针均落入环中的那一刻就是在相同位置的情况,那种情况只可能发生在快慢指针的速率是一样的,那也就不能称之为快慢指针了,与我们的架设前提不服,因此在此不做讨论
1:快指针与慢指针之间差一步。此时继续往后走,慢指针前进一步,快指针前进两步,两者相遇。
2:快指针与慢指针之间差两步。此时继续往后走,慢指针前进一步,快指针前进两步,两者之间相差一步,转化为第一种情况。
3:快指针与慢指针之间差N步。此时继续往后走,慢指针前进一步,快指针前进两步,两者之间相差(N+1-2)-> N-1步。因此,此题得证。所以快指针必然与慢指针相遇。
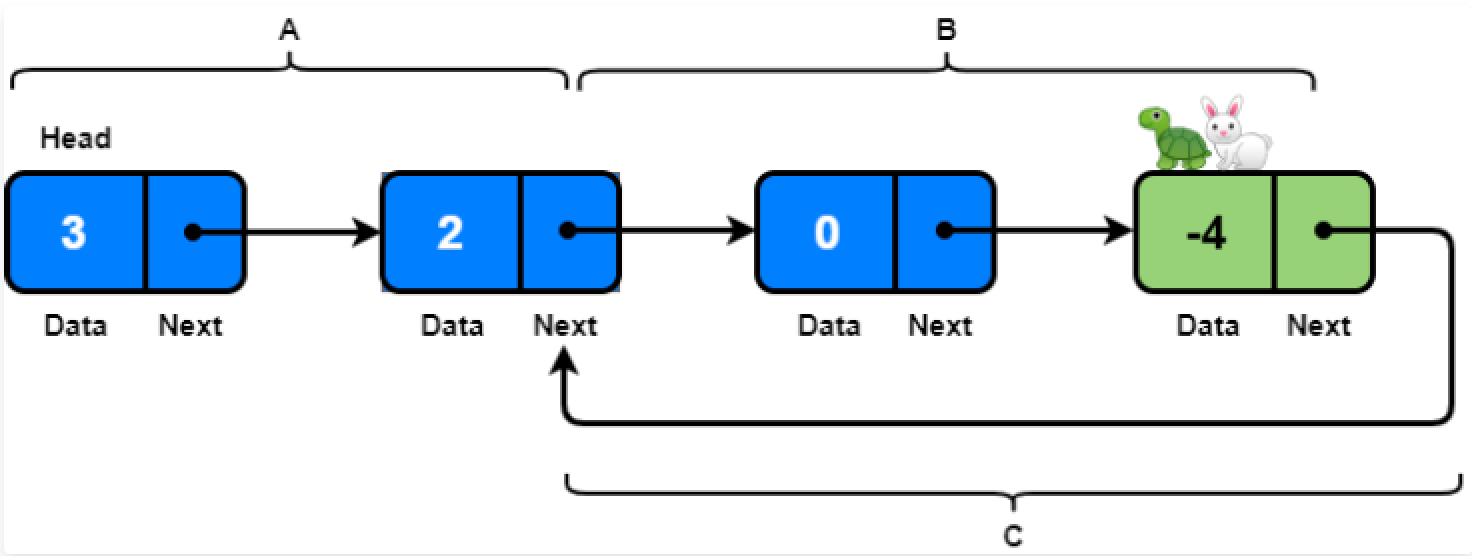
我们简化为如下的数学模型,假设快慢指针在绿点相遇;假定快指针在环中绕了
P圈在绿点与慢指针相遇,慢指针在环中绕了Q圈在绿点与快指针相遇。我们可以计算出:
快指针走的路程为:
S(快指针路程) = A + (P+1)*B + P*C慢指针走的路程为:
S(慢指针路程) = A + (Q+1)*B + Q*C又因为快指针是慢指针速率的
X倍,因此可得出:
S(快指针路程) = X*S(慢指针路程),即
A + (P+1)*B + P*C = X*{A + (Q+1)*B + Q*C}
P>Q && P,Q均要尽量小[因为是第一次相遇]当快指针的速率为慢指针的速率的两倍时,即
X = 2
(P-2Q)(B+C) = A+B==>(P-2Q-1)(B+C) + C = A假定环长为D,即
D=B+C,则:
(P-2Q-1)D + C = A且P>Q && P,Q均要尽量小[因为是第一次相遇]当要查找环的起点时,就需要用到上述结论;即当找到相遇节点之后,用一个指针从相遇节点开始往后走,一个节点从头开始走,当两者相等时候即为链表环的起点。
通过上面的结论我们可以轻松解决,判断链表中是否有环以及如何找到对应环的起始点;并且利用快慢指针也能快速找到等分点(最经典的就是二等分点即中点)等问题,可以再刷几道题实战一下,双指针算法基本原理和实践
欢迎关注
H寻梦人公众号,更多精彩博文!!!


