【python机器学习:朴素贝叶斯分类算法】
朴素贝叶斯介绍
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。分类算法的内容是要求给定特征, 让我们得出类别,这也是所有分类问题的关键。那么如何由指定特征,得到我们最终的类别,也是我们下面要讲的,每一个不同的分类算法,对应着不同的核心思想。朴素贝叶斯法是基于贝叶斯定理与特征条件独立性假设的分类方法。对于给定的训练集,首先基于特征条件独立假设学习输入输出的联合概率分布(朴素贝叶斯法这种通过学习得到模型的机制,显然属于生成模型);然后基于此模型,对给定的输入 x,利用贝叶斯定理求出后验概率最大的输出 y。
贝叶斯公式
P(B[j]|A[i])=P(A[i]|B[j])P(B[j]) / P(A[i])
换个表达形式就会明朗很多,如下:

朴素贝叶斯是贝叶斯证据独立的表达形式,属于一种特例。实际应用过程中贝叶斯表达式非常复杂,但是我们希望把它拆分成多个朴素贝叶斯来表达,这样能够快速获得后验概率。
基本思想
贝叶斯决策理论是主观贝叶斯派归纳理论的重要组成部分。贝叶斯决策就是在不完全情报下,对部分未知的状态用主观概率估计,然后用贝叶斯公式对发生概率进行修正,最后再利用期望值和修正概率做出最优决策。其基本思想是:
1. 已知类条件概率密度参数表达式和先验概率。
2. 利用贝叶斯公式转换成后验概率。
3. 根据后验概率大小进行决策分类。
未知事件中A[i]出现时B[j]出现的后验概率在主观上等于已有事件中B[j]出现时A[i]出现的先验概率值乘以B[j]出现的先验概率值然后除以A[i]出现的先验概率值最终得到的结果。这就是贝叶斯的核心思想:用先验概率估计后验概率。
这么说可能有些抽象了,接下来我们来说一个例子吧,一个分类问题中很经典的例子。
示例分析
数据展示


现在给我们的问题是,有一天你想出去打球,但是你在犹豫,你想先看看今天的环境再说,环境的你看中的主要特征是天气、温度、湿度、和风度。
这是一个典型的分类问题,转为数学问题就是比较p(去打球|(天气、温度、湿度、风度))与p(不去打球|(天气、温度、湿度、风度))的概率,谁的概率大,我就能给出去或者不去的答案!
又根据朴素贝叶斯公式
P(B[j]|A[i])=P(A[i]|B[j])P(B[j]) / P(A[i]
我们可以得到
p
(
去
打
球
∣
(
天
气
、
温
度
、
湿
度
、
风
度
)
)
=
p
(
(
天
气
、
温
度
、
湿
度
、
风
度
)
∣
去
打
球
)
p
(
天
气
、
温
度
、
湿
度
、
风
度
)
\begin{array}{c} {p(去打球|(天气、温度、湿度、风度))}= \frac{p((天气、温度、湿度、风度)|去打球)}{p(天气、温度、湿度、风度)} \end{array}
p(去打球∣(天气、温度、湿度、风度))=p(天气、温度、湿度、风度)p((天气、温度、湿度、风度)∣去打球)
我们需要求{p((去打球|(天气、温度、湿度、风度)},这是我们不知道的,但是通过朴素贝叶斯公式可以转化为好求的三个量.
- p ( 天 气 、 温 度 、 湿 度 、 风 度 ) ∣ 去 打 球 ) {p(天气、温度、湿度、风度)|去打球)} p(天气、温度、湿度、风度)∣去打球)
- p ( 天 气 、 温 度 、 湿 度 、 风 度 ) ) {p(天气、温度、湿度、风度)) } p(天气、温度、湿度、风度))
-
p
(
去
打
球
)
{ p(去打球)}
p(去打球)
其实这也就是我们的先验概率 和条件概率了
先验概率和条件概率
算的结果应该是下面这样的,具体的计算就不算了,应该能看懂
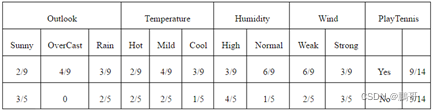
算法步骤:
1)收集数据;
2)准备数据:需要数值型或布尔型数据。如果是文本文件,要解析成词向量
3)分析数据:有大量特征时,用直方图分析效果更好;
4)训练算法:计算不同的独立特征的条件概率;
5)测试算法:计算错误率;
6)使用算法:一个常见的朴素贝叶斯应用是文档分类。
代码
具体的代码如下
首先我们先计算先验概率和条件概率
计算先验概率和条件概率
# -*- coding: utf-8 -*-
"""
Created on Fri Apr 1 19:32:19 2022
@author: jason
@email: jason9@vip.qq.com
@Software:python3.7.6+spyder4.2.5
@description:
"""
import numpy as np
import pandas as pd
import copy
df = pd.read_csv('./data.csv', encoding='gbk')
Yes_dict = {}
No_dict = {}
def addtwodimdict(thedict, key_a, key_b, val):
if key_a in thedict.keys():
if key_b in thedict[key_a].keys():
thedict[key_a].update({key_b: thedict[key_a][key_b]+1})
else:
thedict[key_a].update({key_b: 1})
else:
thedict.update({key_a: {key_b: 1}})
def count_total():
'''play的总数,要么玩,要么不玩
{'Yes': 9, 'No': 5} 14'''
count = {}
total = 0
for result in ['Yes', 'No']:
'''因为天气要么有风要么无风,可以用 这两种特征来统计总数'''
if result == "Yes":
count[result] = Yes_dict["Windy"][False] + Yes_dict["Windy"][True]
elif result == "No":
count[result] = No_dict["Windy"][False] + No_dict["Windy"][True]
total += count[result]
return count, total
def count_base_rates():
"""计算先验概率"""
categories, simpleTotal = count_total()
print(categories, simpleTotal)
for i in Yes_dict:
for j in Yes_dict[i]:
Yes_dict[i][j] = Yes_dict[i][j]/categories["Yes"]
# print(Yes_dict[i][j])
if j not in No_dict[i].keys():
continue
No_dict[i][j] = No_dict[i][j]/categories["No"]
# print(Yes_dict)
# print(No_dict)
if __name__ == "__main__":
# {'Outlook': {'overcast': 4, 'rain': 3, 'sunny': 2}, 'Temperature': {'hot': 2, 'mild': 4, 'cool': 3}, 'Humidity': {'high': 3, 'normal': 6}, 'Windy': {False: 6, True: 3}}
# {'Outlook': {'sunny': 3, 'rain': 2}, 'Temperature': {'hot': 2, 'cool': 1, 'mild': 2}, 'Humidity': {'high': 4, 'normal': 1}, 'Windy': {False: 2, True: 3}}"""
# for j in df.iloc[:,:-1]:
# Yes_dict[j]={}
# No_dict[j]={}
# print(df)
# 统计数目
for i in range(0, len(df)):
for j in df.iloc[:, :-1]:
if df.iloc[i]["Play"] == "yes":
addtwodimdict(Yes_dict, j, df.iloc[i][j], 0)
elif df.iloc[i]["Play"] == "no":
addtwodimdict(No_dict, j, df.iloc[i][j], 0)
""""读取数据"""
count_base_rates()
计算结果如下
"""{'Outlook':
{'overcast': 0.4444444444444444,
'rain': 0.3333333333333333,
'sunny': 0.2222222222222222},
'Temperature':
{'hot': 0.2222222222222222,
'mild': 0.4444444444444444,
'cool': 0.3333333333333333},
'Humidity':
{'high': 0.3333333333333333,
'normal': 0.6666666666666666},
'Windy':
{False: 0.6666666666666666,
True: 0.3333333333333333}}
{'Outlook':
{'sunny': 0.6,
'rain': 0.4},
'Temperature':
{'hot': 0.4,
'cool': 0.2, 'mild': 0.4},
'Humidity':
{'high': 0.8,
'normal': 0.2},
'Windy': {False: 0.4,
True: 0.6}}
"""
结果展示如下:

分类
基于上述计算得到先验概率和条件概率,实现对于任意给定的未知样本(如“Sunny, Hot, High, False”)计算其属于各个类别的概率。
def count_like(data):
'''计算后验概率,带值计算'''
# test_data={'Outlook': 'overcast',
# 'Temperature': 'hot',
# 'Humidity': 'normal',
# 'Windy': True}
categories, total = count_total()
likelihold = {}
print("#####先验概率#######")
print(Yes_dict)
print("#####先验概率#######")
print(No_dict)
print("#####要分类数据#######")
print(data)
for i in ['Yes', 'No']:
likelihold[i] = 1
if i == "Yes":
for j in data:
if data[j] not in Yes_dict[j]:
#说明没有这个特征,直接不可能
likelihold[i] = 0
break
else:
likelihold[i] *= Yes_dict[j][data[j]]/categories[i]
print("条件概率"+str(Yes_dict[j][data[j]])+"/"+str(categories[i]))
likelihold[i] *= categories[i]/total
# print(likelihold)
for j in data:
if likelihold [i]==0:
break
likelihold[i] /=( Yes_dict[j][data[j]]+ No_dict[j][data[j]])/total
# print(likelihold)
print("总体概率"+str(Yes_dict[j][data[j]])+"/"+str(total))
print(likelihold)
elif i == "No":
for j in data:
if data[j] not in No_dict[j]:
#说明没有这个特征,直接不可能
likelihold[i] = 0
break
else:
likelihold[i] *= No_dict[j][data[j]]/categories[i]
print("条件概率"+str(No_dict[j][data[j]])+"/"+str(categories[i]))
likelihold[i] *= categories[i]/total
for j in data:
if likelihold [i]==0:
break
likelihold[i] /=( Yes_dict[j][data[j]]+ No_dict[j][data[j]])/total
print("总体概率"+str(No_dict[j][data[j]])+"/"+str(categories[i]))
# print(likelihold)
print(likelihold)
print("类别为: ",end="")
if likelihold["Yes"]>likelihold["No"]:
print("Yes")
else:
print("No")
return likelihold
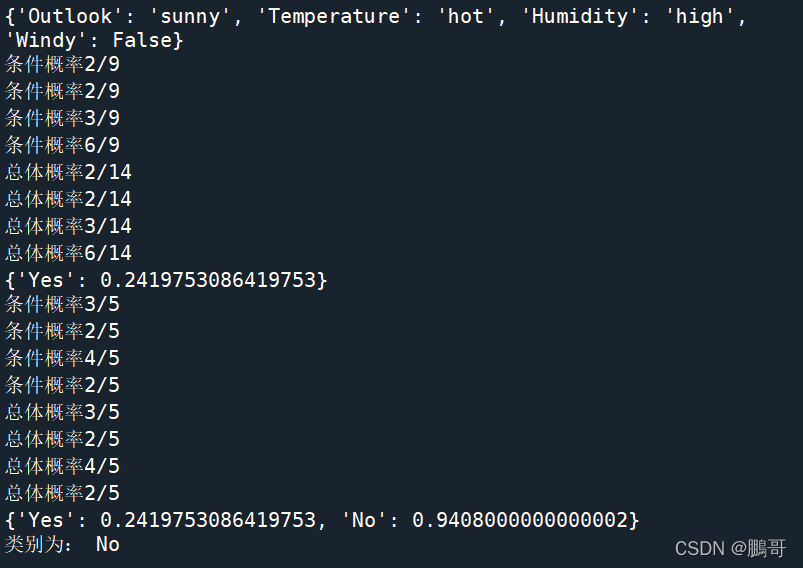
结果展示

 浙公网安备 33010602011771号
浙公网安备 33010602011771号