毕设(4)—关节空间轨迹规划(多项式)
毕设中用到了很多代码,其中一部分我通过看书和看论文学习并实现的代码,会通过Gitee仓库分享出来,这些代码仅用于学习使用,祝各位毕业生顺利完成毕设!
毕设系列内容:毕业设计——四自由度机械臂轨迹规划
毕设(4)—关节空间轨迹规划(多项式)
机械臂在关节空间中的轨迹规划适用于点到点、实时控制等场景,可以用函数来控制关节角度的变化,在本文中采用三次和五次多项式实现轨迹规划。
三次多项式轨迹规划
三次多项式的角度、角速度、角加速度的函数如下形式
\[\left\{
\begin{array}{l}
\theta(t)=a_0+a_1t+a_2t^2+a_3t^3 \\
\dot{\theta}(t)=a_1+2a_2t+3a_3t^2 \\
\ddot{\theta}(t)=2a_2+6a_3t
\end{array}
\right.
\]
对函数施加约束,设起始角度和终止角度分别为\(q_1\)和\(q_2\),起始速度和终止速度分别为\(v_1\)和\(v_2\),运动的起始时刻为0,终止时刻为t,则有以下约束
\[\left\{
\begin{array}{l}
\theta(0)=q_1=a_0 \\
\theta(t)=q_2=a_0+a_1t+a_2t^2+a_3t^3 \\
\dot{\theta}(0)=v_1=a_1 \\
\dot{\theta}(t)=v_2=a_1+2a_2t+3a_3t^2
\end{array}
\right.
\]
求解约束,可以得到\(a_0\)到\(a_3\)的多项式系数如下
\[\left\{
\begin{array}{l}
a_0=q_1 \\
a_1=v_1 \\
a_2=\frac{-3q_1+3q_2-2v_1t-v_2t}{t^2} \\
a_3=\frac{2q_1-2q_2+v_1t+v_2t}{t^3}
\end{array}
\right.
\]
这个系数只适用于起始时刻为0的情况,在面对起始时刻不是0的情况,可以用时间相减的方法来适配。
五次多项式轨迹规划
跟三次多项式差不多
角度、角速度、角加速度函数如下形式
\[\left\{
\begin{array}{l}
\theta(t)=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5 \\
\dot{\theta}(t)=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4 \\
\ddot{\theta}(t)=2a_2+6a_3t+12a_4t^2+20a_5t^3
\end{array}
\right.
\]
约束条件为
\[\left\{
\begin{array}{l}
\theta(0)=q_1=a_0 \\
\theta(t)=q_2=a_0+a_1t+a_2t^2+a_3t^3+a_4t^4+a_5t^5 \\
\dot{\theta}(0)=v_1=a_1 \\
\dot{\theta}(t)=v_2=a_1+2a_2t+3a_3t^2+4a_4t^3+5a_5t^4 \\
\ddot{\theta}(0)=A_1=2a_2 \\
\ddot{\theta}(t)=A_2=2a_2+6a_3t+12a_4t^2+20a_5t^3
\end{array}
\right.
\]
求解约束得到
\[\left\{
\begin{array}{l}
a_0=q_1 \\
a_1=v_1 \\
a_2=\frac{A1}{2} \\
a_3=\frac{-20q_1+20q_2-12v_1t-8v_2t-3A_1t^2+A_2t^2}{2t^3} \\
a_4=\frac{30q_1-30q_2+16v_1t+14v_2t+3A_1t^2-2A_2t^2}{2t^4} \\
a_5=\frac{-12q_1+12q_2-6v_1t-6v_2t-A_1t^2+A_2t^2}{2t^5}
\end{array}
\right.
\]
Matlab代码验证
代码有点长,具体函数代码可以到仓库中自行查找
test3.m
clear, clc, close all;
L(1) = Link([0 0 0 0 0 0], 'modified');
L(2) = Link([0 0 0 -pi / 2 0 0], 'modified');
L(3) = Link([0 0 135 0 0 0], 'modified');
L(4) = Link([0 0 147 0 0 0], 'modified');
L(5) = Link([0 131 61 -pi / 2 0 0], 'modified');
robot = SerialLink(L, 'name', 'Dobot');
angle1 = [-pi / 6, -pi / 6, pi / 3, -pi / 6, pi / 4];
angle2 = [pi / 3, -pi / 60, pi / 30, -pi / 60, -pi / 4];
angleT = [angle1; angle2];
VT = [0, 0, 0, 0, 0; 0, 0, 0, 0, 0];
AT = [0, 0, 0, 0, 0; 0, 0, 0, 0, 0];
%[q, qd, qdd, t] = cubic_traj(angleT, VT, [0, 5], 100);
[q, qd, qdd, t] = quintic_traj(angleT, VT, AT, [0, 5], 100);
qdeg=rad2deg(q);
qddeg = rad2deg(qd);
qdddeg = rad2deg(qdd);
figure(1);
T = zeros(4, 4, size(q, 1));
for i = 1:size(q, 1)
T(:, :, i) = myfkine(q(i, :));
end
plot3(squeeze(T(1, 4, :)), squeeze(T(2, 4, :)), squeeze(T(3, 4, :)), 'r-', 'LineWidth', 2);
title('轨迹图');
hold on;
plot3(squeeze(T(1,4,1)),squeeze(T(2,4,1)),squeeze(T(3,4,1)), 'bo', 'MarkerSize', 7, 'LineWidth', 2);
hold on;
plot3(squeeze(T(1,4,size(q, 1))),squeeze(T(2,4,size(q, 1))),squeeze(T(3,4,size(q, 1))), 'bo', 'MarkerSize', 7, 'LineWidth', 2);
hold on;
robot.plot(q);
grid on;
hold on;
figure(2);
plot(t,qdeg);
title('角度图');
legend('q_1', 'q_2', 'q_3', 'q_4', 'q_5');
xlabel('t(s)');
ylabel('deg(°)');
grid on;
hold on;
figure(3);
plot(t, qddeg);
title('角速度图');
legend('q_1', 'q_2', 'q_3', 'q_4', 'q_5');
xlabel('t(s)');
ylabel('V(°/s)');
grid on;
hold on;
figure(4);
plot(t, qdddeg);
title('角加速度图');
legend('q_1', 'q_2', 'q_3', 'q_4', 'q_5');
xlabel('t(s)');
ylabel('A(°/s^2)');
grid on;
hold on;
三次多项式运行结果如下
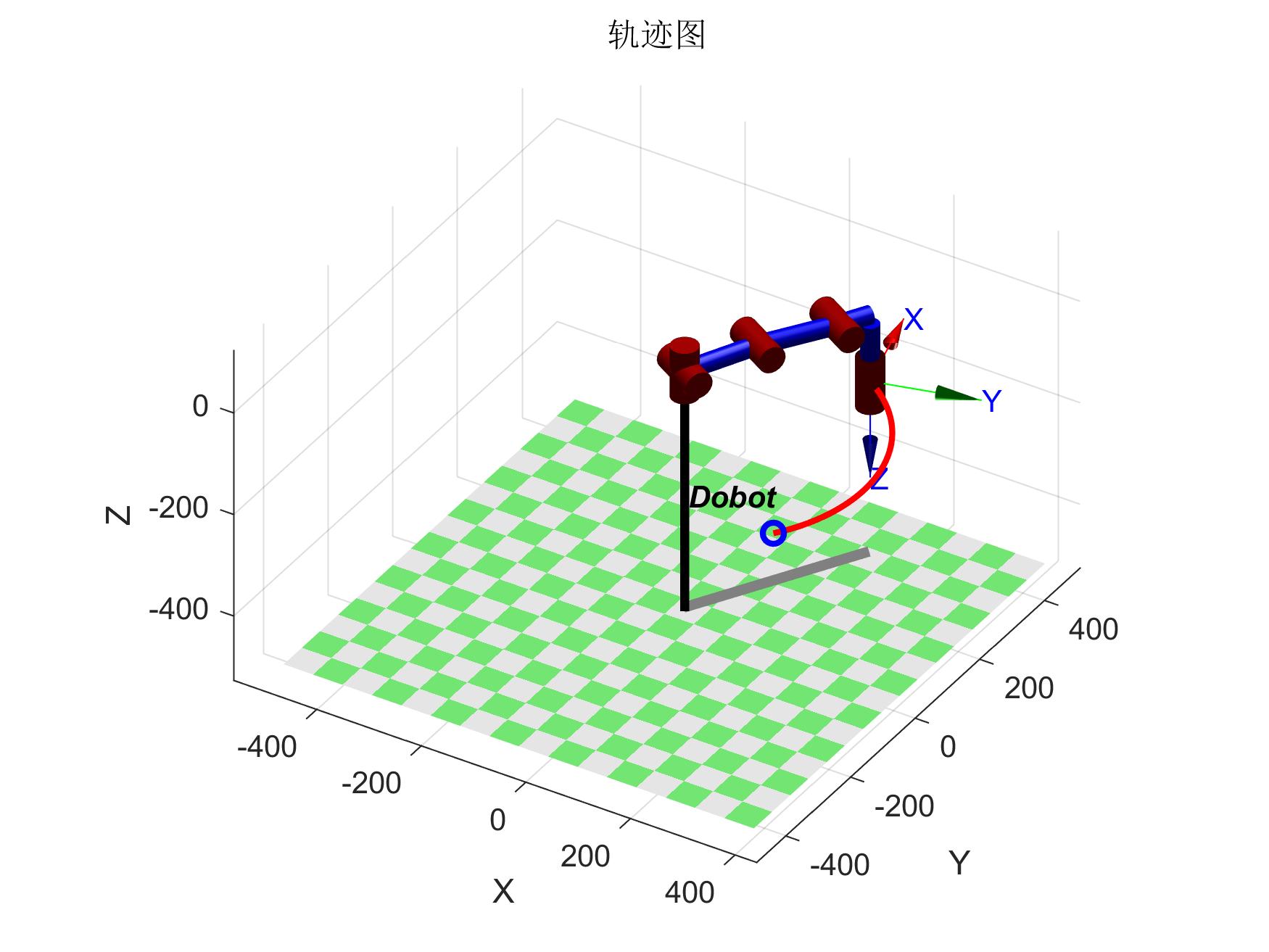 三次轨迹图 三次轨迹图 |
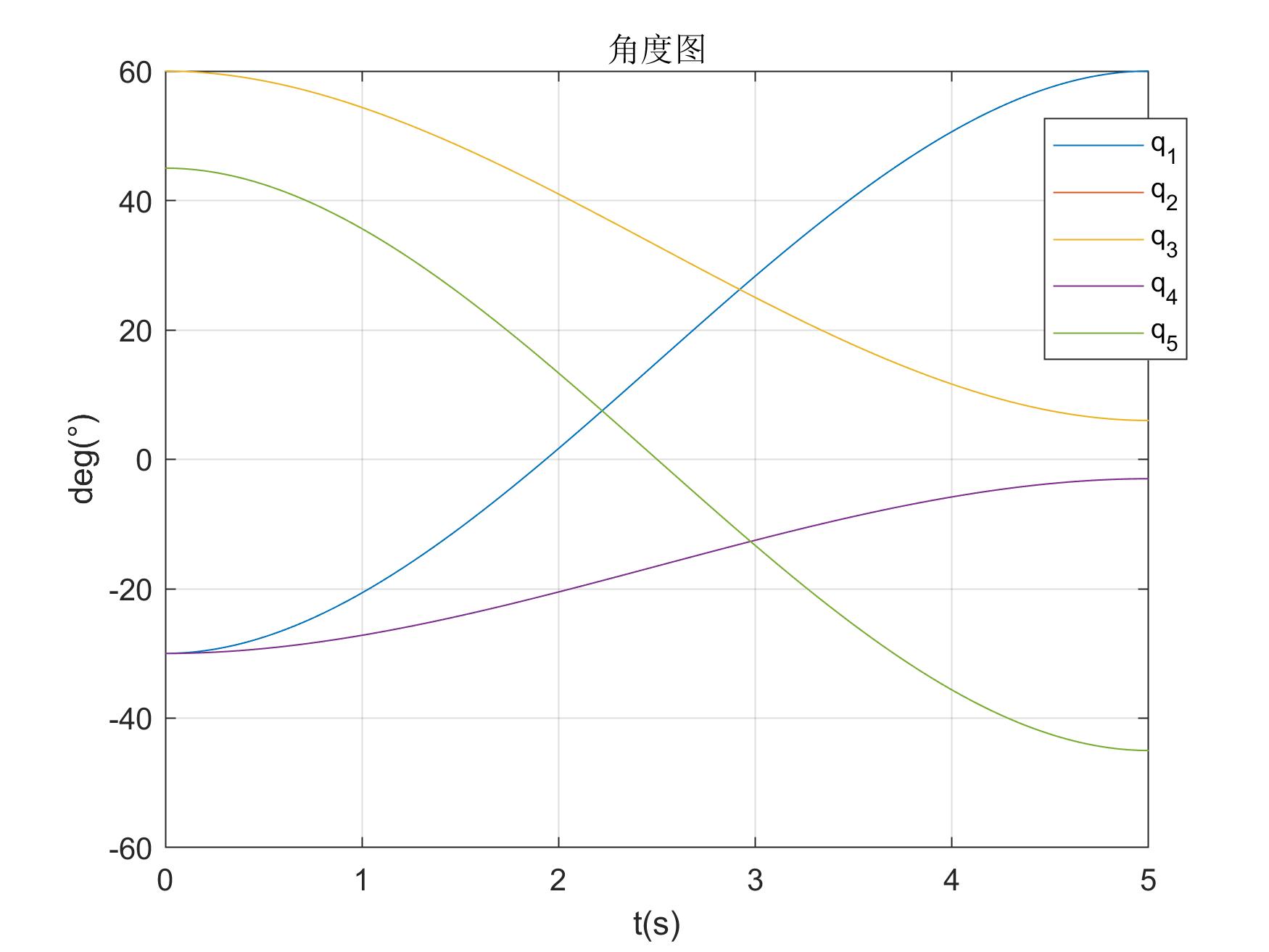 三次角度图 三次角度图 |
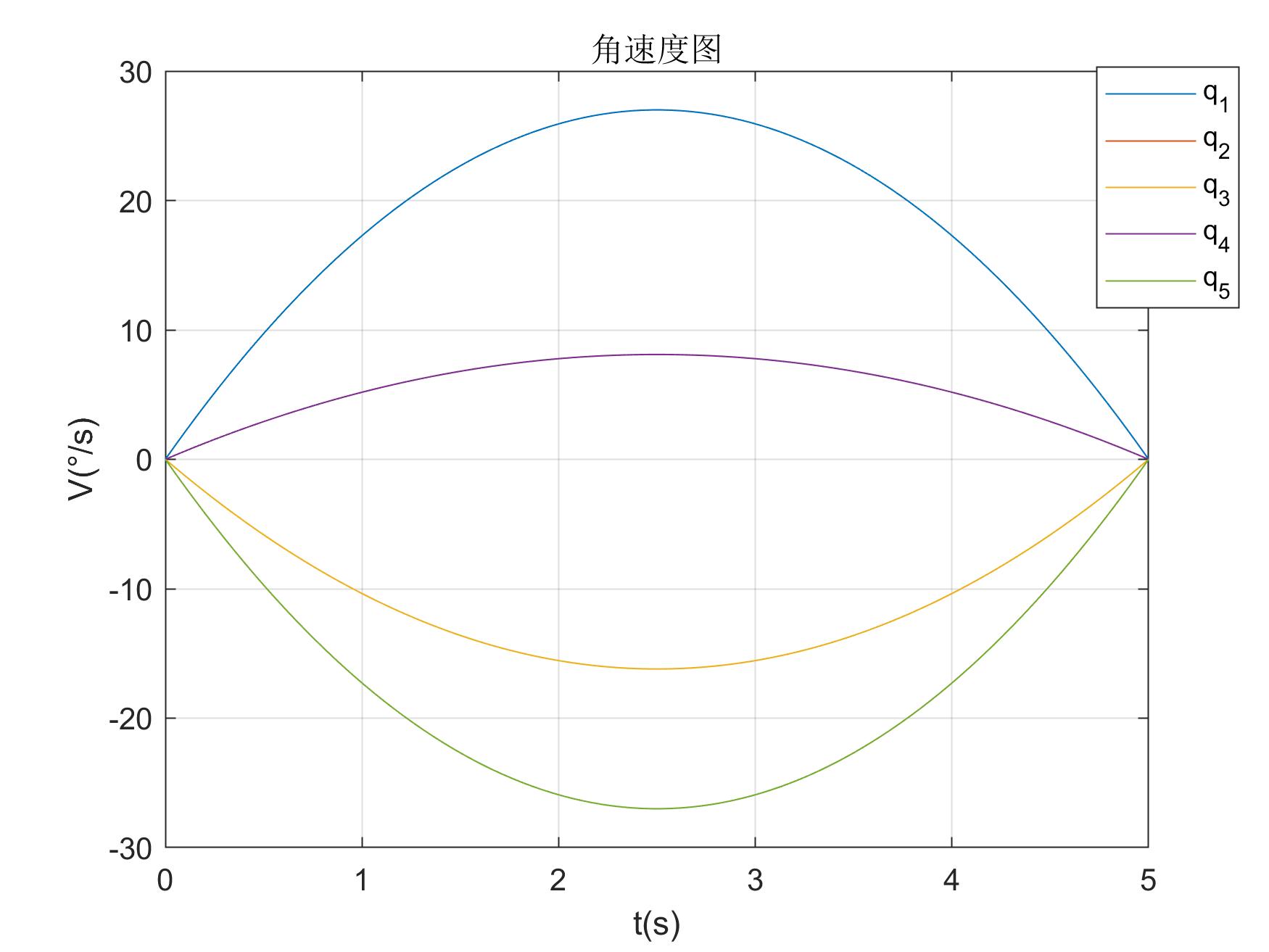 三次角速度图 三次角速度图 |
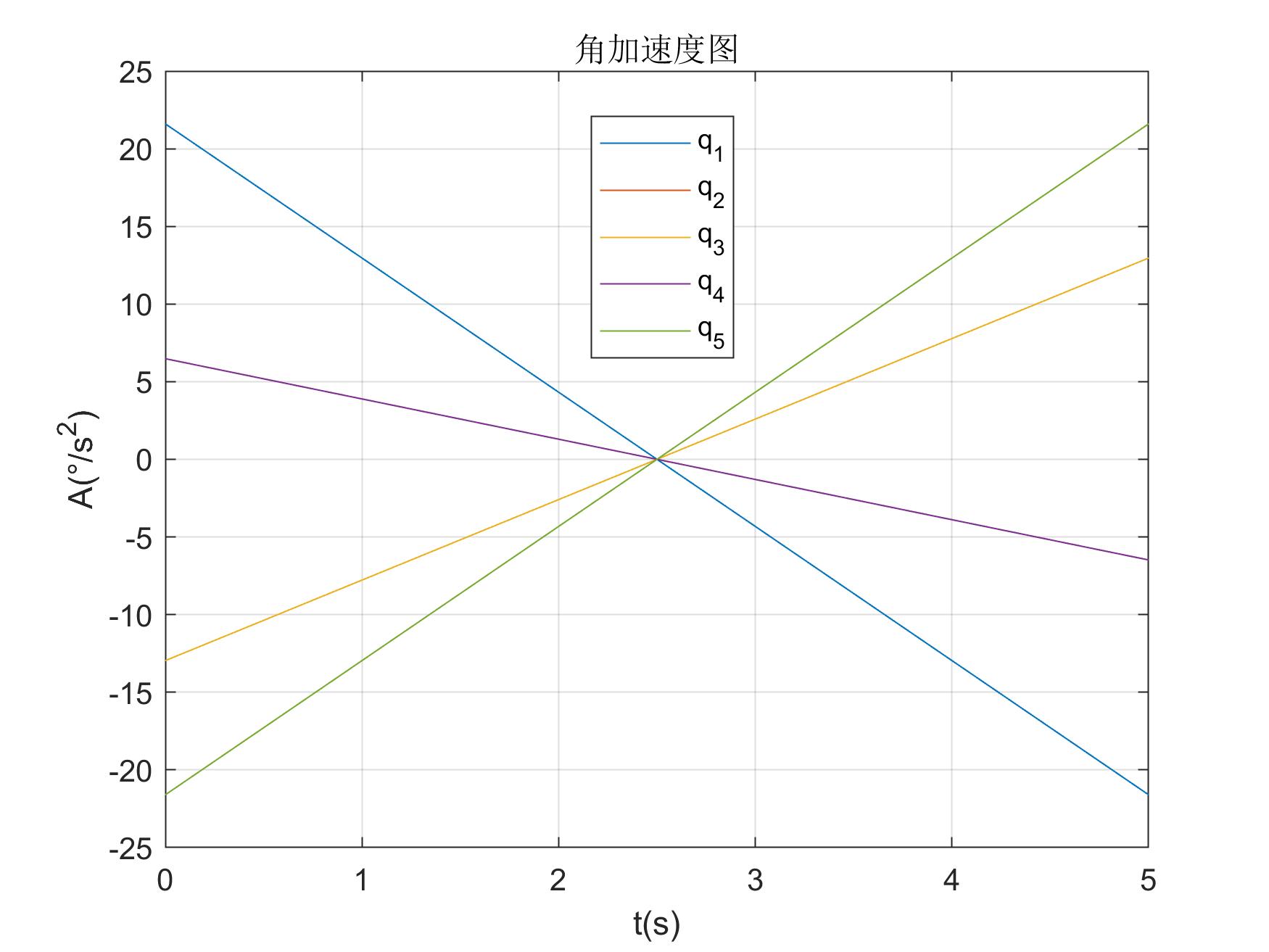 三次角加速度图 三次角加速度图 |
五次多项式运行结果如下
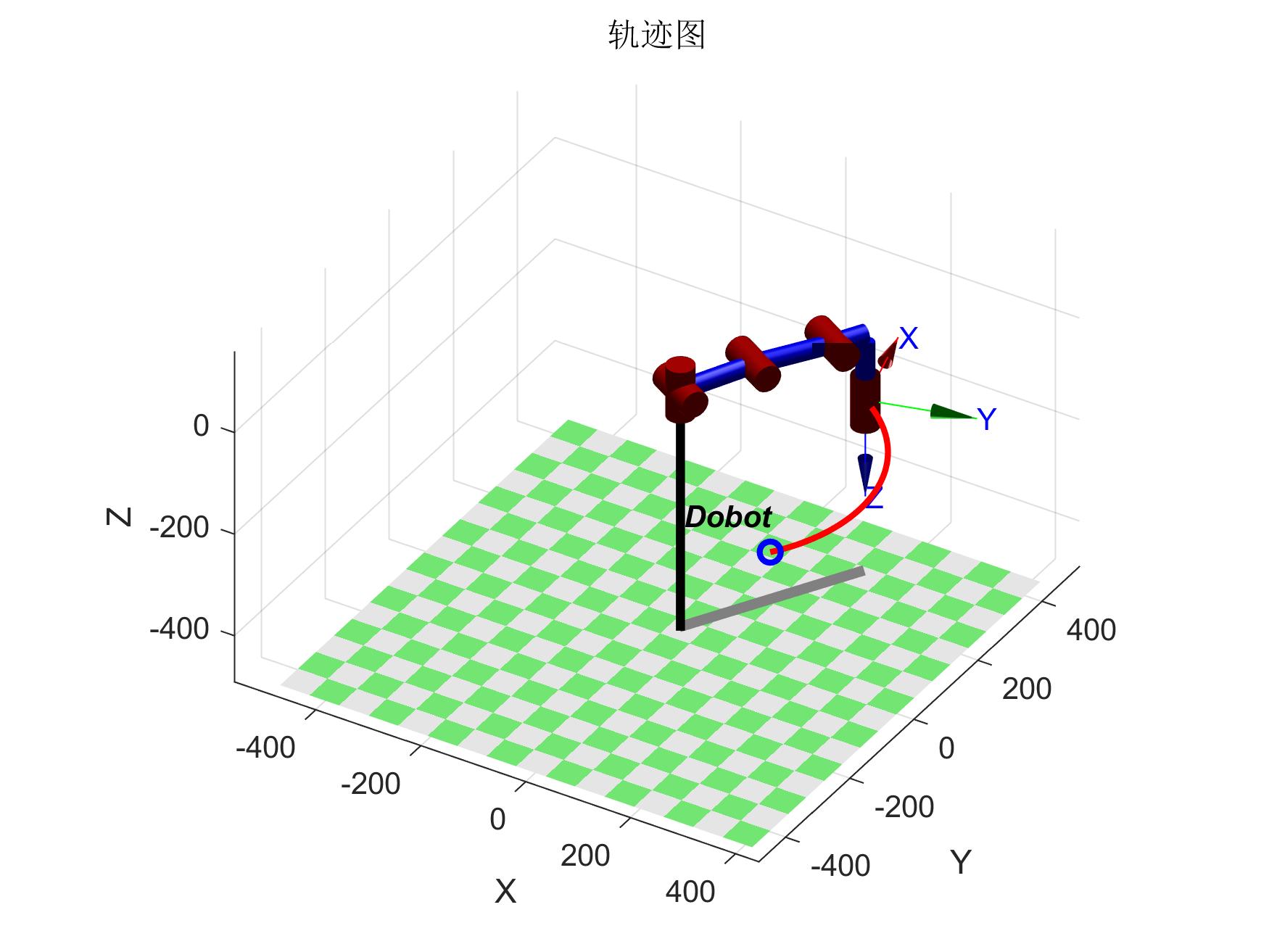 五次轨迹图 五次轨迹图 |
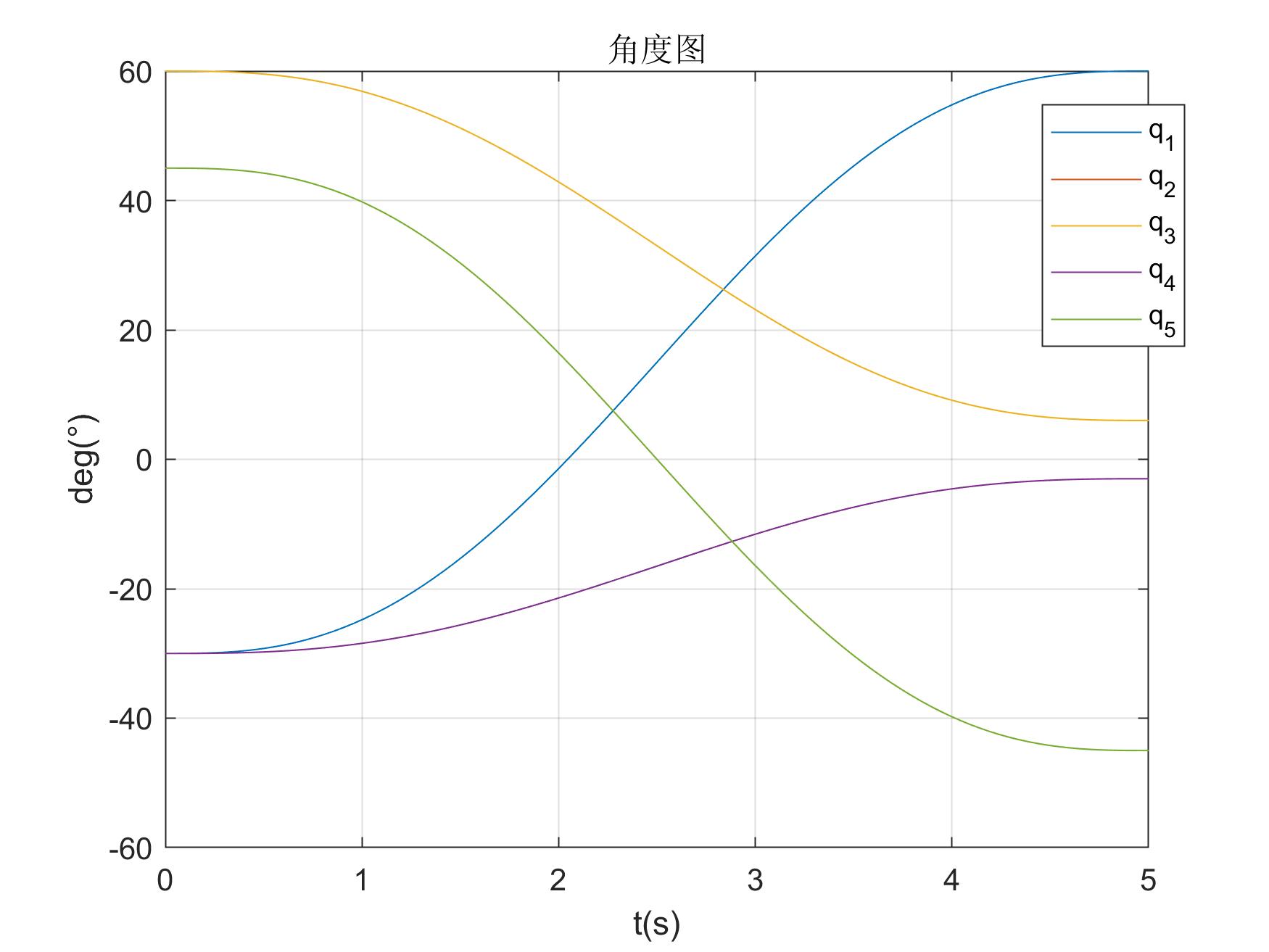 五次角度图 五次角度图 |
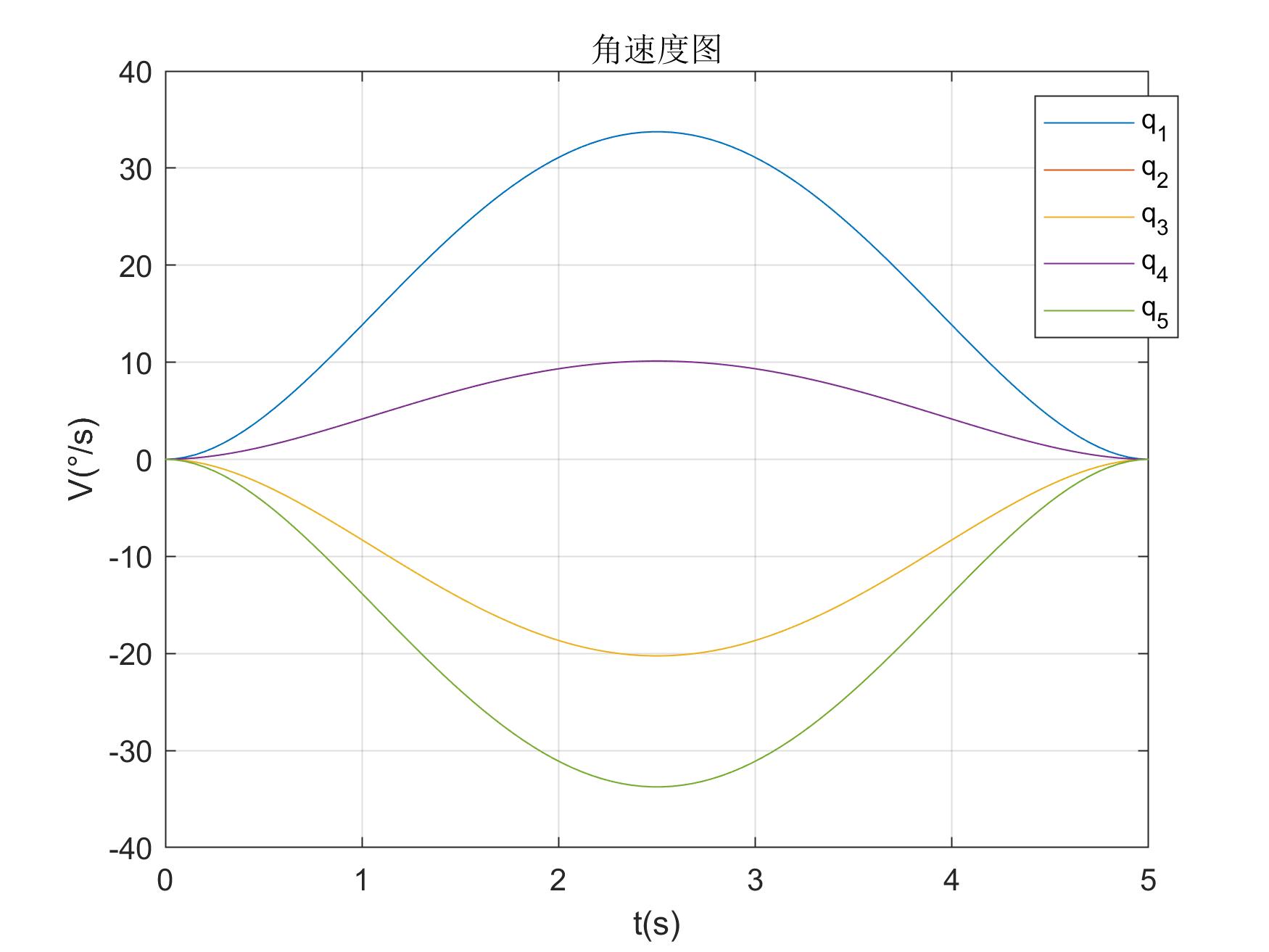 五次角速度图 五次角速度图 |
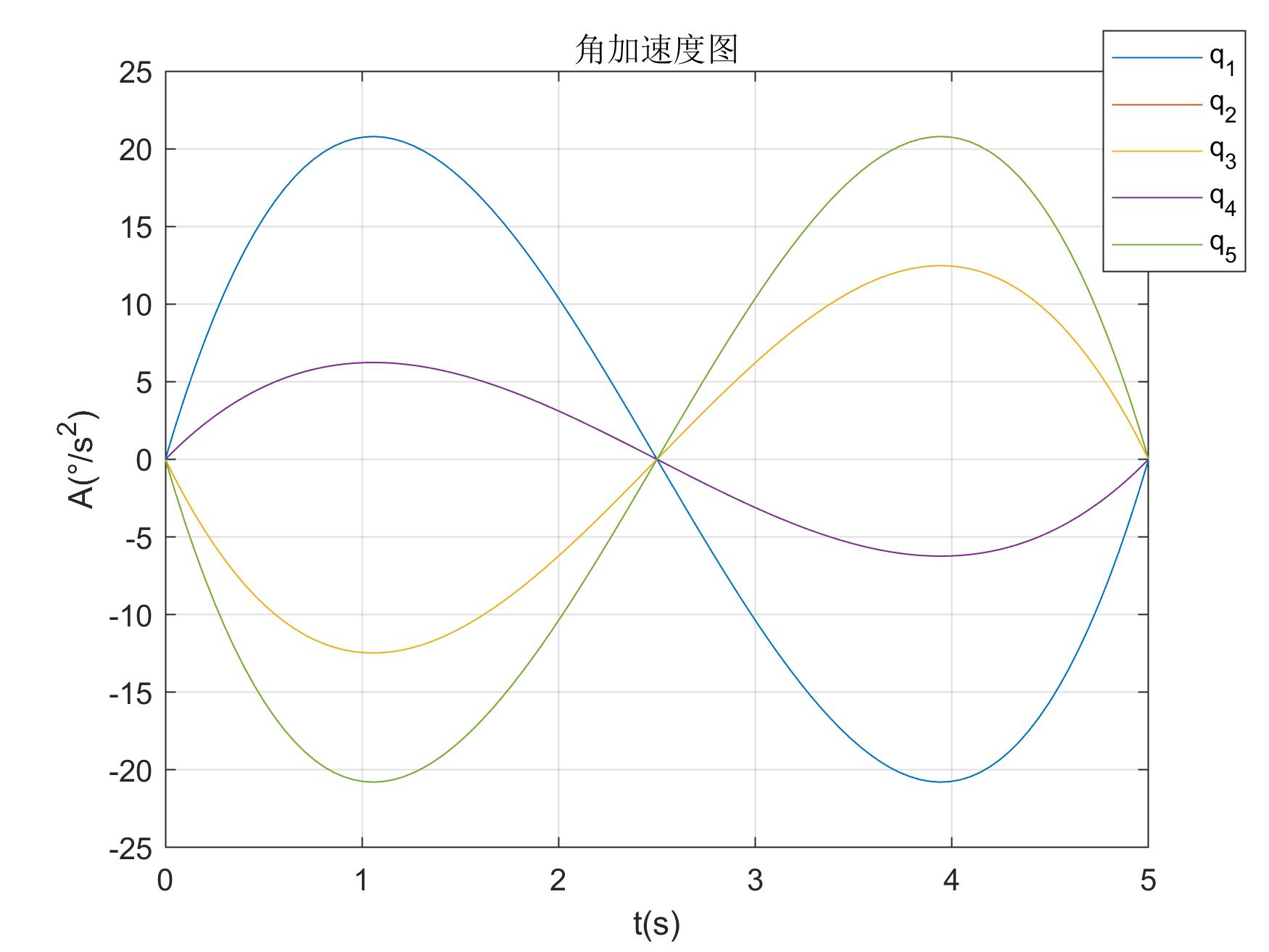 五次角加速度图 五次角加速度图 |
本文到此结束,后续会继续更新的~😃
作者:Dragonet-Z
出处:https://www.cnblogs.com/dragonet-Z/p/16337461.html
版权声明:本博客所有文章除特殊声明外,均遵循BY-NC-SA许可协议,转载请注明出处!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号