动态规划入门(1)：最长递增子序列

__________________________工作学习之余，一边听歌，一边推敲。人生一大快事!

不断修炼自己读代码的能力。

眉眼初抬，且看最长递增子序列。

设长度为N的数组为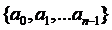，则假定以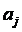结尾的数组序列的最长递增子序列长度为L(j)，则。

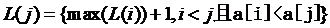也就是说，我们需要遍历在j之前的所有位置i(从0到j-1)，找出满足条件a[i]<a[j]的L(i)，求出max(L(i))+1即为L(j)的值。

最后，我们遍历所有的L(j)（从0到N-1），找出最大值即为最大递增子序列。时间复杂度为O(N^2)。

例如给定的数组为{5，6，7，1，2，8}，则L(0)=1, L(1)=2, L(2)=3, L(3)=1, L(4)=2, L(5)=4。所以该数组最长递增子序列长度为4，序列为{5，6，7，8}。

my codes:

 

#include<bits/stdc++.h>
#define len(a) (sizeof(a) / sizeof(a[0])) 
//求取数组长度优秀预定义
using namespace std;
int lis(int a[],int len)
{
    int dp[len];
    for(int i=0;i<len;i++) dp[i]=1;

    for(int j=1;j<len;j++)
    {
        for(int i=0;i<j;i++)
        {
            if(a[i]<a[j] && dp[j]<dp[i]+1)
                dp[j]=dp[i]+1;
        }
    }

    int max=0;
    for(int j=0;j<len;j++)
    {
        if(dp[j]>max) max=dp[j];
    }
    return max;
}
int main()
{
    int a[]={5,6,7,1,2,8};
    int res=lis(a,len(a));
    cout<<res<<endl;
    return 0;
}

 my codes2:

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n;
    cin>>n; 
    int tmp;
    vector<int> queue;
    vector<int> dp(n,1);
    for(int i=0;i<n;i++)
    {
        cin>>tmp;
        queue.push_back(tmp);
    }
    for(int i=1;i<n;i++)
    {
        for(int j=0;j<i;j++)
        {
            if(queue[i]>queue[j] && dp[i]<dp[j]+1) 
                    dp[i]=dp[j]+1;
        }
    }

    int max=0;
    for(int i=0;i<n;i++)
    {
        if(dp[i]>max) max=dp[i]; //注意细节哦，行百里者半九十！是>号哦！ 
    }
    cout<<max<<endl;
    return 0;
}

 

 牛刀小试：

https://www.nowcoder.com/practice/6d9d69e3898f45169a441632b325c7b4?tpId=37&tqId=21247&tPage=2&rp=&ru=%2Fta%2Fhuawei&qru=%2Fta%2Fhuawei%2Fquestion-ranking

 

 

参考：

https://blog.csdn.net/u013178472/article/details/54926531