期望入门之快速幂介绍1

--------------------------------------------------------------岁月不饶人，我亦未曾饶过岁月。

https://blog.csdn.net/Cassie_zkq/article/details/97255683

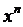
迭代快速幂法：

使用公式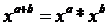，我们可以将 n 写成一些正整数的和，,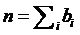

如果n的二进制表示有k位，第i位为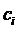（非0即1），那么有：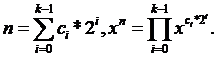

 

 

codes:

double myPow(double x,int n)
{
	long long N=n;
	if(N<0){
		x,int=1/x;
		N=-N;
	}
	double ans=1;
	double current_product=x;
	for(long long i=N;i;i/=2){
		if((i%2)==1){
			ans*=current_product;
		}
		current_product*=current_product;
	}
	return ans;
}

仍然等待着很多很多的去理解！去结合知乎上的一篇很精炼的文章。

 

递归快速幂算法：

时间复杂度与空间复杂度具为.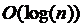

 

double fastPow(double x,long long n)
{
	if(n==0) return 1.0;
	double half=fastPow(x,n/2);
	if(n%2==0) return half*half;
	else return half*half*x;
}
double myPow(double x,int n)
{
	long long N=n;
	if(N<0)
	{
		x=1/x;
		N=-N;
	}
	return fastPow(x,N);
}

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

https://blog.csdn.net/Cassie_zkq/article/details/97255683