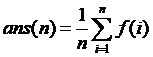期望入门之剑指三秦
————————————————————不畏浮云遮望眼，只缘身在最高层。
——————————————aim:
题目地址：http://acm.hdu.edu.cn/showproblem.php?pid=6595
https://www.cnblogs.com/zxcoder/p/11253099.html
https://blog.csdn.net/Cassie_zkq/article/details/97255683
Everything is generated in equal probability
逆序数( Inverse number )：
在一个排列中，如果一对数的前后位置与大小顺序相反，即前面的数大于后面的数，那么它们就称为一个逆序。
一个排列中逆序的总数就称为这个排列的逆序数。
逆序数为偶数的排列称为偶排列;逆序数为奇数的排列称为奇排列。
如2431中，21，43，41，31是逆序，逆序数是4，为偶排列。
一个长度为n的全排列，逆序数的期望应该是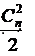 
，[也可以写成这样的形式：
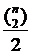]，即任取两个数产生逆序数的期望为
。
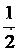全排列的子序列离散化之后也是一个全排列。
对于一个长度为i的原序列，可以产生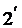
个子序列（包括长度为0的空序列在内的）。它的长度为j的子序列有
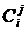个，且概率都是
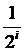。对于这个长度为j的子序列，它又可以当作一个原序列得到它的子序列，同理，它的子序列也可以当成一个原序列得到子序列。。。。所以这是一个很深的问题，但是我们可以用递推解决，依据是期望的可加性。
对于一个长度为i的原序列，它长度为j的子序列对应的逆序对数目的期望值已经求得，那么在求原序列逆序对的期望值时可以用到这个结果，不难推出下面这个式子：
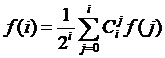，变形为：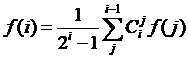
。
这样就可以O()预处理得到所有的长度为i的原序列对应的逆序对数目的期望值,f(i)是取模后的结果。
针对题目有：
