线段树入门之夜空星亮

--------------------------------------------不是能不能办到的问题，既然我已经下定决心要成为海贼王了，如果因此而战死的话，也无所谓了。

承接上一章节，继续探索线段树丫！

如何利用线段树进行区间统计?

假设这13个数为1,2,3,4,1,2,3,4,1,2,3,4,1. （A[1]=1,A[2]=2,......A[13]=1）在区间之后标上该区间的数字之和：

 

 

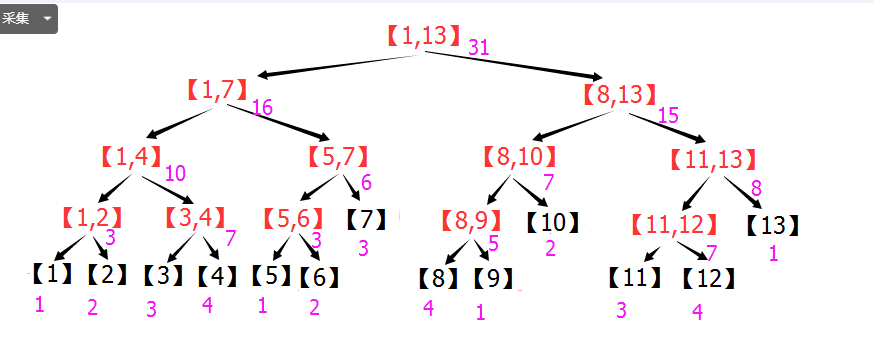
如果要计算[2,12]的和，按照之前的算法：

 

[2,12]=[2] + [3,4] + [5,7] + [8,10] + [11,12]

 

  29  = 2 + 7 + 6 + 7 + 7

 

计算5个数的和就可以算出[2,12]的值。

 嘻嘻，下面介绍另一个问题:

如何进行点修改?

以上一个图为讨论的基础:

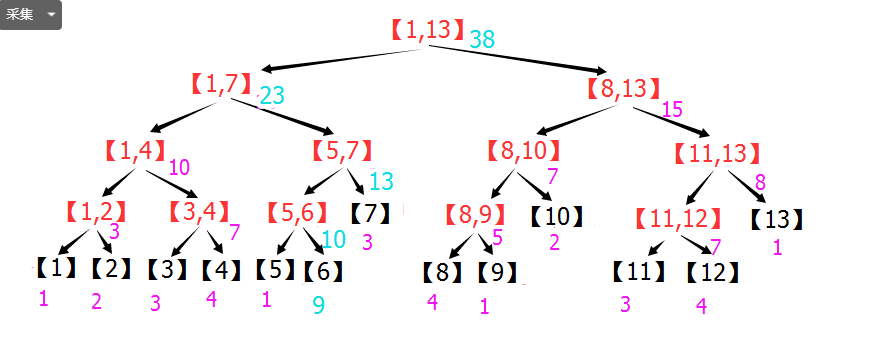
假设把A[6]+=7 ,看看哪些区间需要修改？[6],[5,6],[5,7],[1,7],[1,13]这些区间全部都需要+7.其余所有区间都不用动。

于是，这颗线段树中，点修改最多修改5个线段树元素（每层一个）。

下图中，修改后的元素用蓝色表示。

 

一身转战三千里，且去追寻线段树的存储结构:

线段树是一种二叉树，当然可以像一般的树那样写成结构体，指针什么的。

但是它的优点是，它也可以用数组来实现树形结构，可以大大简化代码。

数组形式适合在编程竞赛中使用，在已经知道线段树的最大规模的情况下，直接开足够空间的数组，然后在上面建立线段树。

简单的记法： 足够的空间 = 数组大小n的四倍。

实际上足够的空间 =  （n向上扩充到最近的2的某个次方）的两倍。

举例子：假设数组长度为5，就需要5先扩充成8，8*2=16.线段树需要16个元素。如果数组元素为8，那么也需要16个元素。
所以线段树需要的空间是n的两倍到四倍之间的某个数，一般就开4*n的空间就好，如果空间不够，可以自己算好最大值来省点空间。

 

怎么用数组来表示一颗二叉树呢？假设某个节点的编号为v,那么它的左子节点编号为2*v，右子节点编号为2*v+1。

然后规定根节点为1.这样一颗二叉树就构造完成了。通常2*v在代码中写成 v<<1 。 2*v+1写成 v<<1|1 。