杭电oj初体验之 Code

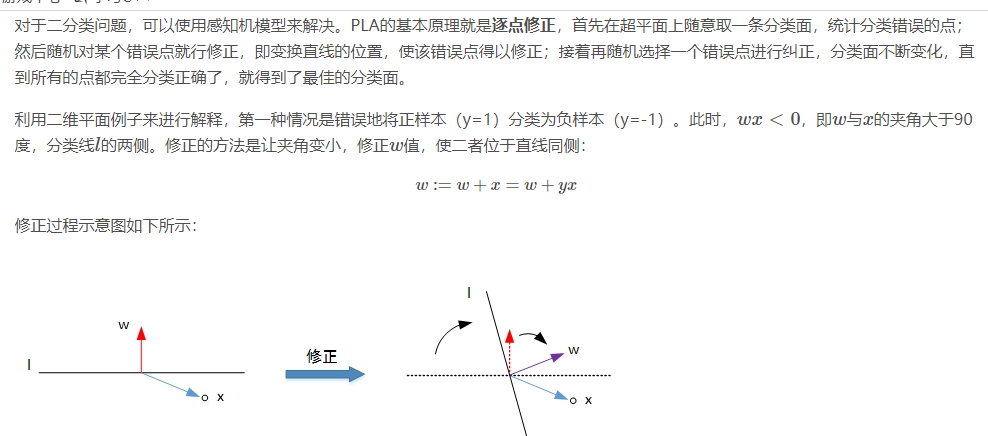
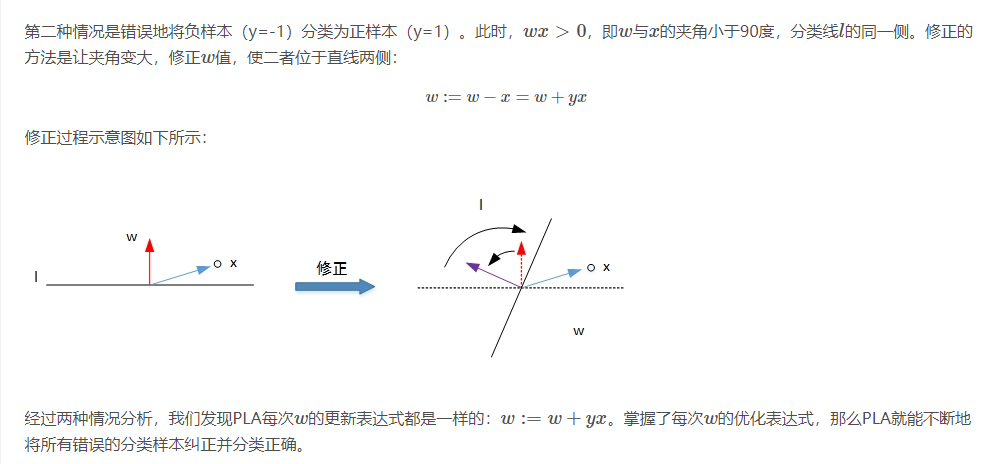
PLA算法：

https://blog.csdn.net/red_stone1/article/details/70866527

 

 The problem:

Analysis:

题目链接可见：https://vjudge.net/contest/313395#problem/M

Reference codes:

#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

const int N = 105;

int n;

int sgn(long long x) {
    return (x > 0) - (x < 0);
}

struct P {
    long long d[3];
    long long& operator[](int x) {
        return d[x];
    }
    P () {}
    P (long long a, long long b, long long c) {
        d[0] = a; d[1] = b; d[2] = c;
    }
};

struct node {
    P x;
    int y;
} p[N];

P operator+(P a, P b) {
    P c;
    for (int i = 0; i < 3; i++)
        c[i] = a[i] + b[i];
    return c;
}

P operator-(P a, P b) {
    P c;
    for (int i = 0; i < 3; i++)
        c[i] = a[i] - b[i];
    return c;
}

P operator*(int a, P b) {
    P c;
    for (int i = 0; i < 3; i++)
        c[i] = a * b[i];
    return c;
}

bool operator<(P a, P b) {
    return a[1] < b[1] || (a[1] == b[1] && a[2] < b[2]);
}

long long operator*(P a, P b) {
    return a[1] * b[2] - a[2] * b[1];
}

long long operator^(P a, P b) {
    return a[1] * b[1] + a[2] * b[2];
}

long long det(P a, P b, P c) {
    return (b - a) * (c - a);
}

struct L {
    P a, b;
    L () {}
    L (P x, P y) {
        a = x; b = y;
    }
};

bool onSeg(P p, L s) {
    return sgn(det(p, s.a, s.b)) == 0 && sgn((s.a - p) ^ (s.b - p)) <= 0;
}

vector<P> convex(vector<P> p) {
    vector<P> ans, S;
    for (int i = 0; i < p.size(); i++) {
        while (S.size() >= 2
                && sgn(det(S[S.size() - 2], S.back(), p[i])) <= 0)
                    S.pop_back();
        S.push_back(p[i]);
    }
    ans = S;
    S.clear();
    for (int i = (int)p.size() - 1; i >= 0; i--) {
        while (S.size() >= 2
                && sgn(det(S[S.size() - 2], S.back(), p[i])) <= 0)
                    S.pop_back();
        S.push_back(p[i]);
    }
    for (int i = 1; i + 1 < S.size(); i++)
        ans.push_back(S[i]);
    return ans;
}

bool PointInPolygon(P p, vector<P> poly) {
    int cnt = 0;
    for (int i = 0; i < poly.size(); i++) {
        if (onSeg(p, L(poly[i], poly[(i + 1) % poly.size()]))) return true;
        int k = sgn(det(poly[i], poly[(i + 1) % poly.size()], p));
        int d1 = sgn(poly[i][2] - p[2]);
        int d2 = sgn(poly[(i + 1) % poly.size()][2] - p[2]);
        if (k > 0 && d1 <= 0 && d2 > 0) cnt++;
        if (k < 0 && d2 <= 0 && d1 > 0) cnt--;
    }
    if (cnt != 0) return true;
    return false;
}

bool SegmentIntersection(L l1, L l2) {
    long long c1 = det(l1.a, l1.b, l2.a), c2 = det(l1.a, l1.b, l2.b);
    long long c3 = det(l2.a, l2.b, l1.a), c4 = det(l2.a, l2.b, l1.b);
    if (sgn(c1) * sgn(c2) < 0 && sgn(c3) * sgn(c4) < 0) return true;
    if (sgn(c1) == 0 && onSeg(l2.a, l1)) return true;
    if (sgn(c2) == 0 && onSeg(l2.b, l1)) return true;
    if (sgn(c3) == 0 && onSeg(l1.a, l2)) return true;
    if (sgn(c4) == 0 && onSeg(l1.b, l2)) return true;
    return false;
}

bool ConvexHullDivide(vector<P> p1, vector<P> p2) {
    for (int i = 0; i < p1.size(); i++)
        if (PointInPolygon(p1[i], p2))
            return false;
    for (int i = 0; i < p2.size(); i++)
        if (PointInPolygon(p2[i], p1))
            return false;
    for (int i = 0; i < p1.size(); i++)
        for (int j = 0; j < p2.size(); j++)
            if (SegmentIntersection(L(p1[i], p1[(i + 1) % p1.size()]), L(p2[j], p2[(j + 1) % p2.size()])))
                return false;
    return true;
}

bool check() {
    vector<P> p1, p2;
    for (int i = 1; i <= n; i++) {
        if (p[i].y == 1)
            p1.push_back(p[i].x);
        else
            p2.push_back(p[i].x);
    }
    vector<P> c1, c2;
    c1 = convex(p1);
    c2 = convex(p2);
    if (ConvexHullDivide(c1, c2)) return true;
    return false;
}

int f(P w, P x) {
    long long sum = 0;
    for (int i = 0; i < 3; i++)
        sum += w[i] * x[i];
    return sgn(sum);
}

void PLA() {
    P w = P(0, 0, 0);
    int i = 1, cnt = 0;
    long long cc = 0;
    while (true) {
        cc++;
        if (f(w, p[i].x) != p[i].y) {
            w = w + p[i].y * p[i].x;
            cnt = 0;
        }
        else {
            if (++cnt == n) break;
        }
        i = i + 1;
        if (i > n) i -= n;
    }
    cout << cc << endl;
}

int main() {
    int testcase;
    cin >> testcase;
    while (testcase--) {
        cin >> n;
        for (int i = 1; i <= n; i++) {
            cin >> p[i].x[1] >> p[i].x[2] >> p[i].y;
            p[i].x[0] = 1;
        }
        if (!check())
            puts("Infinite loop!");
        else {
            puts("Successful!");
        }
    }
    return 0;
}