均分糖果

题目描述

有N堆糖果，编号分别为1，2，...，N。每堆上有若干个，但糖果总数必为N的倍数。可以在任一堆上取若干个糖果，然后移动。

移动规则为：在编号为1的堆上取的糖果，只能移到编号为2的堆上；在编号为N的堆上取的糖果，只能移到编号为N-1的堆上；其他堆上取的糖果，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上糖果数都一样多。

例如N=4，4堆糖果数分别为：

①　9　②　8　③　17　④　6

移动3次可达到目的：

从③取4个糖放到④（9 8 13 10）->从③取3个糖放到②（9 11 10 10）->从②取1个糖放到①（10 10 10 10）。

输入描述:

每个测试文件包含多组测试数据，每组输入的第一行输入一个整数N（1<=N<=100），表示有N堆糖果。

接下来一行输入N个整数A1 A2...An，表示每堆糖果初始数，1<=Ai<=10000。

输出描述:

对于每组输入数据，输出所有堆均达到相等时的最少移动次数。

示例1

输入

4
9 8 17 6

输出

3
codes:

 

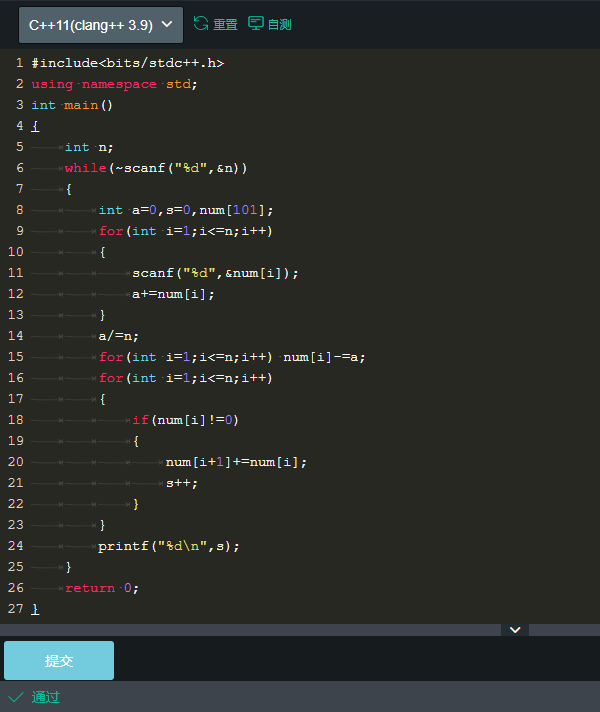
Thoughts:

贪心，每堆糖果数减去平均，从左向右扫描，不为0的加到右边一堆（正数相当于右移，负数相当于左移），同时移动次数加一。

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。