非整除集合

今天天光明媚，在牛客网上刷到了一个关于挖掘数的余数性质的好题，特特记录之!

问题说明:给定一个由正整数组成的集合S，找出一个最大的子集合S·，使得S·中任意两个数字的和都不能被K整除。例如S=「10，10，12，19，22，24，25」，K=4。S·的可能取值为「10，12，25」或者「19，22，25」等，S·最多只能取3个数。

输入描述:

输入为两行，第一行两个数字，分别表示集合S的元素数量N和K。第二行为N个数字，分别是S的各个元素值。

1<N<1e5

1<K<100

1<S[i]<1e9

输出描述:

输出为一个数字，集合S·的最大长度。
我一开始是并没有什么想法的。在浏览大神们的代码时我发现了这一种做法。它的精神我尽量地用我的一些理解来概括：将集合中的数有序存储于一个向量中。在建立一个依附于此向量的
每一个元素的关于k的余数向量数组。统计各余数的出现次数。接下来一个循环判断遍历余数向量数组问题得以解决。当然，这个遍历语句很有一种对称形的美感。它基于的关于数的性质是:........
（好吧，我还尚且不能内化语言描述出来，希望有没有大神能解释一下他的性质!）

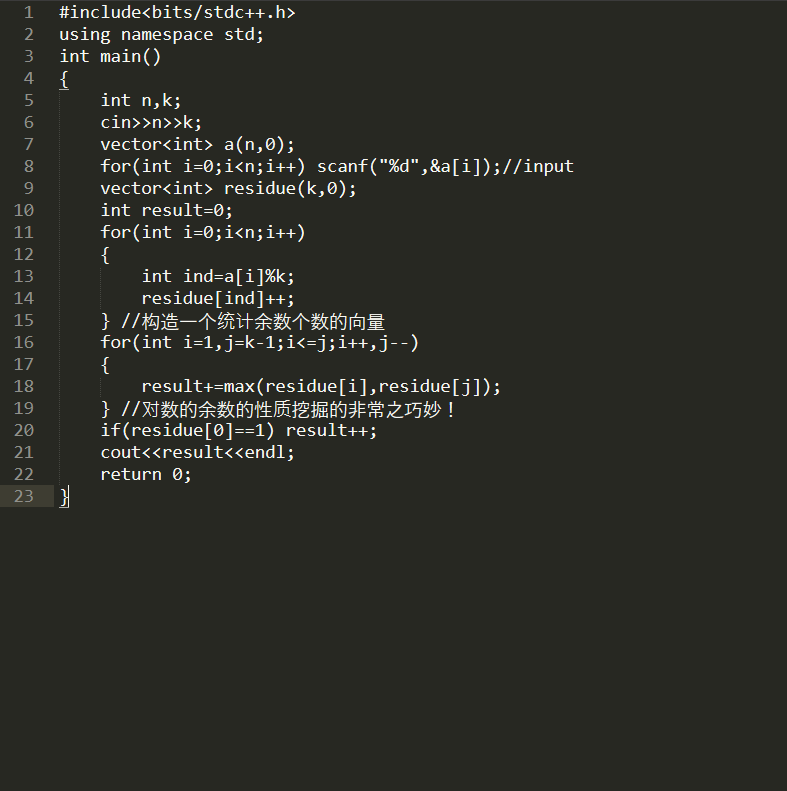
运行结果是:

 对啦，题目的叙述还是有一些问题的。关于集合的性质有一点是要去澄明的:集合之元素各各互异。

关于数学知识的一些叙述呈现于此:

对于模m同余的数组成由模m决定的数类。而且只要在式子mq+r里让q通过所有的整数，我们就得到这个类里的所有数。

一个类的任意数，对于同一个类的所有数而言，都叫做模m的剩余。当q=0时，我们得到的剩余正好等于余数r,叫做非负的最小剩余。

从每个类取一个剩余，我们得到模m的一个完全剩余组。