从头开始使用梯度下降优化在Python中实现单变量多项式回归(后续2)
绩效分析(SGD与BGD)
模型性能分析是根据以下指标完成的:
=>平均绝对误差:实例样本的预测值与实际观测值之间的平均mod(差)。
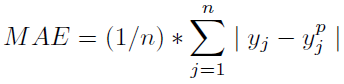
查找MAE:
ae = 0 # Absolute Error
for i in range(0,y_train.shape[0]):
ae = ae + abs(training_predictions[i] - y_train[i])
MAE = ae/y_train.shape[0] # Mean Absolute Error
=>均方误差:实例样本的预测值与实际观测值之间的平方差的平均值。

查找MSE:
from math import *
se = 0 # Square Error
for i in range(0,y_train.shape[0]):
se = se + pow((training_predictions[i] - y_train[i]), 2)
MSE = se/y_train.shape[0] # Mean Square Error
=>均方根误差:实例样本的预测值与实际观测值之间的平方差的平均值的平方根。

查找RMSE:
from math import *
RMSE = sqrt(MSE) # Root Mean Square Error
=> R平方得分或确定系数:


import numpy as np
y_m = np.mean(y_train)SStot = 0
for i in range(0,y_train.shape[0]):
SStot = SStot + pow((y_train[i] - y_m), 2)SSres = 0
for i in range(0,y_train.shape[0]):
SSres = SSres + pow((y_train[i] - training_predictions[i]), 2)R_Square_Score = 1 - (SSres/SStot)
SGD和BGD之间的比较:

因此,批次梯度下降在各个方面均明显胜过随机梯度下降!
这就是使用Scratch中的Gradient Descent在Python中实现单变量线性回归的全部内容。



