2019 Multi-University Training Contest 5
2019 Multi-University Training Contest 5
A
题意:对于 \(a \equiv bx \pmod{p}\) ,给出 p 和 x,求找到一组 a 和 b,使得 \(a<b\) 且 b 最小。 \(T \le 2 \times 10^5, 3 \le p \le 10^{15}\) , p 是质数。
key:类欧
化简 \(bx \bmod p < b\) ,易得 \(1 \le \lfloor\frac{bx}{p}\rfloor-\lfloor\frac{b(x-1)}{p}\rfloor\) ,翻译成人话就是求最小的 b ,使得 \((bx/p,b(x-1)/p)\) 之间存在一个整数。直接上类欧板子
#include<bits/stdc++.h>
using namespace std;
typedef __int128 LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef pair<LL,int> pli;
const int SZ = 1e6 + 10;
const int INF = 1e9 + 10;
const int mod = 1e9 + 7;
const LD eps = 1e-8;
LL read() {
LL n = 0;
char a = getchar();
bool flag = 0;
while(a > '9' || a < '0') { if(a == '-') flag = 1; a = getchar(); }
while(a <= '9' && a >= '0') { n = n * 10 + a - '0',a = getchar(); }
if(flag) n = -n;
return n;
}
LL solve(LL a,LL b,LL c,LL d) {
if(a/b<c/d) return 1;
if(a>=b||c>=d) return solve(a%b,b,c%d,d);
LL x = a / b;
LL t = solve(d,c,b,a);
// printf("%lld %lld %lld %lld: %lld\n",a,b,c,d,t*b/a);
return t*d/c+1;
}
int main() {
int T = read();
while(T --) {
LL p = read(),x = read();
LL A = x-1,B = p,C = x,D = p;
LL b = solve(A,B,C,D);
LL a = b * x % p;
printf("%lld/%lld\n",(long long)a,(long long)b);
}
}
改了一下板子,a/b<x/y<c/d 时,先 y 最小,再 x 最小。
void solve(LL a,LL b,LL c,LL d,LL &x,LL &y) {
LL z = (a+b-1)/b;
if(z<=c/d) { x=z; y=1; return ; }
a -= (z-1) * b; c -= (z-1) * d;
solve(d,c,b,a,y,x);
x += (z-1) * y;
}
B
题意:给两个序列,可以任意打乱顺序,求对应位置的异或值序列字典序最小是多少。 \(n \le 10^5, a_i < 2^{30}\)
key:trie,牛逼套路,贪心
先说一个naive的贪心:在两个 trie 上 dfs ,要保证相同子树尽量合并,此时只会剩下若干个 a 中的值或者若干个 b 中的值,回溯时收集两个子树中剩余点集,能合并就合并。由于每次只会在两个点集上尝试合并,如果每次是暴力较小的一侧,在较大的一侧形成的trie中查询,那么每次在trie上查询都会消掉一对点,所以dfs+查询的复杂度是 \(O(n\log n)\)
题解给了一个牛逼的做法,甚至有了可拓展性:
首先假设元素互不相同(存在相同元素时只需记录出现次数),假设 \(f(x,y)=x \ xor \ y\) ,那么所有的 \(f(a_i,*)\) 互不相同,所以必定存在最小值。同理 \(f(*,b_i)\) 也是。如果把它看成二分图,那么每个点都向另一侧有一条边指向取最优时的结果。
如果每次随机选取一个点开始dfs,那么一定不会形成一个大于 2 的环(因为如果存在 a->b, b->c,这意味着 f(b,c) 优于 f(b,a) ,形成大于 2 的环必然矛盾)。由于搜下去一定会终止,那么此时一定找到一个二元环,可以把它拿出作为一个最优匹配。之后再找最优即可。
具体地说,维护一个栈。当栈为空时,随便丢进去一个点,寻找它的 f 最优解。继续做下去,当栈顶元素找到的最优解已入栈,说明它一定在栈顶第二个,弹出并计算答案。
由于每次寻找最优解都会使一个元素入栈/使两个元素弾栈,所以操作次数是 \(O(n)\) 的(有重复元素时也是如此)。对于此题,复杂度即 \(O(n\log MAXV )\) 。
考虑上述的分析过程:几乎没有用到该题的特殊性质。对于普遍情况,只需要满足:
- \(f(a_i,*), f(*,b_i)\) 互不相同
- 寻找 \(f(a_i,*), f(*,b_i)\) 的最优解可以快速完成
就可以沿用该算法。复杂度是 \(O(n*find\_optimzal)\)
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef pair<LL,int> pli;
const int SZ = 1e5 + 10;
const int INF = 1e9 + 10;
const int mod = 1e9 + 7;
const LD eps = 1e-8;
LL read() {
LL n = 0;
char a = getchar();
bool flag = 0;
while(a > '9' || a < '0') { if(a == '-') flag = 1; a = getchar(); }
while(a <= '9' && a >= '0') { n = n * 10 + a - '0',a = getchar(); }
if(flag) n = -n;
return n;
}
const int MAXN = 2 * 31 * SZ;
struct Trie {
int ch[MAXN][2],sz[MAXN],val[MAXN];
int Tcnt = 0;
void insert(pii v) {
int p = 0;
for(int i = 29;i >= 0;i --) {
int c = v.first >> i & 1;
sz[p] ++;
if(!ch[p][c]) ch[p][c] = ++ Tcnt;
assert(Tcnt < 310 * SZ);
p = ch[p][c];
}
sz[p] ++;
val[p] = v.second;
}
pii find_xor_min(int x) {
int p = 0,ans = 0;
for(int i = 29;i >= 0;i --) {
int c = x >> i & 1;
if(ch[p][c] && sz[ch[p][c]]) p = ch[p][c],ans |= c<<i;
else p = ch[p][c^1],ans |= (c^1)<<i;
}
assert(sz[p]);
return make_pair(ans,val[p]);
}
void erase(int x) {
int p = 0;
for(int i = 29;i >= 0;i --) {
int c = x >> i & 1;
sz[p] --;
p = ch[p][c];
}
sz[p] --;
val[p] = 0;
}
void clear() {
for(int i = 0;i <= Tcnt;i ++) {
sz[i] = 0;
val[i] = 0;
memset(ch[i],0,sizeof ch[i]);
}
Tcnt = 0;
}
}tree[2];
struct haha {
int v,t,type,id;
};
mt19937 rd(time(0));
int randlr(int l,int r) { return rd()%(r-l+1)+l; }
int main() {
int T = read();
while(T --) {
tree[0].clear();
tree[1].clear();
int n;
n = read();
vector<haha> V;
for(int o = 0;o < 2;o ++) {
map<int,int> mp;
for(int i = 1;i <= n;i ++) {
int x = read();
mp[x] ++;
}
for(pii p : mp) {
V.push_back((haha){p.first,p.second,o,V.size()});
}
}
for(int i = 0;i < V.size();i ++) {
tree[V[i].type].insert(make_pair(V[i].v,i));
}
vector<int> ans,ins; ins.resize(V.size());
for(int i = 0;i < V.size();i ++) {
if(V[i].t == 0) continue;
stack<int> S;
S.push(i); ins[i] = 1;
while(S.size()) {
haha u = V[S.top()]; S.pop(); ins[u.id] = 0;
pii p = tree[u.type^1].find_xor_min(u.v);
assert(V[p.second].type != u.type);
if(!ins[p.second]) {
S.push(u.id); S.push(p.second);
ins[u.id] = ins[p.second] = 1;
}
else {
haha v = V[p.second];
ins[v.id] = 0; S.pop();
tree[u.type].erase(u.v);
tree[v.type].erase(v.v);
while(V[u.id].t && V[v.id].t) {
ans.push_back(u.v^v.v);
V[u.id].t --; V[v.id].t --;
}
if(V[u.id].t) {
tree[u.type].insert(make_pair(u.v,u.id));
}
if(V[v.id].t) {
S.push(v.id);
ins[v.id] = 1;
tree[v.type].insert(make_pair(v.v,v.id));
}
}
}
}
sort(ans.begin(),ans.end());
for(int i = 0;i < ans.size();i ++) {
printf("%d%c",ans[i],i+1==ans.size()?'\n':' ');
}
}
return 0;
}
C
辣鸡几何题
D
按 b/a 排序后,每个区间的变化是线性的,只需要对每个区间求解即可。顺序扫过去可以轻松维护解方程所需的系数。
由于分数类常数比较大,所以当时写的T了。其实中间过程可以不用分数类的
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef pair<LL,int> pli;
const int SZ = 1e5 + 10;
const int INF = 1e9 + 10;
const int mod = 1e9 + 7;
const LD eps = 1e-8;
namespace fastIO{
#define BUF_SIZE 100000
#define OUT_SIZE 100000
#define ll long long
//fread->read
bool IOerror=0;
inline char nc(){
static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE;
if (p1==pend){
p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin);
if (pend==p1){IOerror=1;return -1;}
//{printf("IO error!\n");system("pause");for (;;);exit(0);}
}
return *p1++;
}
inline bool blank(char ch){return ch==' '||ch=='\n'||ch=='\r'||ch=='\t';}
inline void read(int &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
inline void read(ll &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (sign)x=-x;
}
inline void read(double &x){
bool sign=0; char ch=nc(); x=0;
for (;blank(ch);ch=nc());
if (IOerror)return;
if (ch=='-')sign=1,ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0';
if (ch=='.'){
double tmp=1; ch=nc();
for (;ch>='0'&&ch<='9';ch=nc())tmp/=10.0,x+=tmp*(ch-'0');
}
if (sign)x=-x;
}
inline void read(char *s){
char ch=nc();
for (;blank(ch);ch=nc());
if (IOerror)return;
for (;!blank(ch)&&!IOerror;ch=nc())*s++=ch;
*s=0;
}
inline void read(char &c){
for (c=nc();blank(c);c=nc());
if (IOerror){c=-1;return;}
}
//getchar->read
inline void read1(int &x){
char ch;int bo=0;x=0;
for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1;
for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar());
if (bo)x=-x;
}
inline void read1(ll &x){
char ch;int bo=0;x=0;
for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1;
for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar());
if (bo)x=-x;
}
inline void read1(double &x){
char ch;int bo=0;x=0;
for (ch=getchar();ch<'0'||ch>'9';ch=getchar())if (ch=='-')bo=1;
for (;ch>='0'&&ch<='9';x=x*10+ch-'0',ch=getchar());
if (ch=='.'){
double tmp=1;
for (ch=getchar();ch>='0'&&ch<='9';tmp/=10.0,x+=tmp*(ch-'0'),ch=getchar());
}
if (bo)x=-x;
}
inline void read1(char *s){
char ch=getchar();
for (;blank(ch);ch=getchar());
for (;!blank(ch);ch=getchar())*s++=ch;
*s=0;
}
inline void read1(char &c){for (c=getchar();blank(c);c=getchar());}
//scanf->read
inline void read2(int &x){scanf("%d",&x);}
inline void read2(ll &x){
#ifdef _WIN32
scanf("%I64d",&x);
#else
#ifdef __linux
scanf("%lld",&x);
#else
puts("error:can't recognize the system!");
#endif
#endif
}
inline void read2(double &x){scanf("%lf",&x);}
inline void read2(char *s){scanf("%s",s);}
inline void read2(char &c){scanf(" %c",&c);}
inline void readln2(char *s){gets(s);}
//fwrite->write
struct Ostream_fwrite{
char *buf,*p1,*pend;
Ostream_fwrite(){buf=new char[BUF_SIZE];p1=buf;pend=buf+BUF_SIZE;}
void out(char ch){
if (p1==pend){
fwrite(buf,1,BUF_SIZE,stdout);p1=buf;
}
*p1++=ch;
}
void print(int x){
static char s[15],*s1;s1=s;
if (!x)*s1++='0';if (x<0)out('-'),x=-x;
while(x)*s1++=x%10+'0',x/=10;
while(s1--!=s)out(*s1);
}
void println(int x){
static char s[15],*s1;s1=s;
if (!x)*s1++='0';if (x<0)out('-'),x=-x;
while(x)*s1++=x%10+'0',x/=10;
while(s1--!=s)out(*s1); out('\n');
}
void print(ll x){
static char s[25],*s1;s1=s;
if (!x)*s1++='0';if (x<0)out('-'),x=-x;
while(x)*s1++=x%10+'0',x/=10;
while(s1--!=s)out(*s1);
}
void println(ll x){
static char s[25],*s1;s1=s;
if (!x)*s1++='0';if (x<0)out('-'),x=-x;
while(x)*s1++=x%10+'0',x/=10;
while(s1--!=s)out(*s1); out('\n');
}
void print(double x,int y){
static ll mul[]={1,10,100,1000,10000,100000,1000000,10000000,100000000,
1000000000,10000000000LL,100000000000LL,1000000000000LL,10000000000000LL,
100000000000000LL,1000000000000000LL,10000000000000000LL,100000000000000000LL};
if (x<-1e-12)out('-'),x=-x;x*=mul[y];
ll x1=(ll)floor(x); if (x-floor(x)>=0.5)++x1;
ll x2=x1/mul[y],x3=x1-x2*mul[y]; print(x2);
if (y>0){out('.'); for (size_t i=1;i<y&&x3*mul[i]<mul[y];out('0'),++i); print(x3);}
}
void println(double x,int y){print(x,y);out('\n');}
void print(char *s){while (*s)out(*s++);}
void println(char *s){while (*s)out(*s++);out('\n');}
void flush(){if (p1!=buf){fwrite(buf,1,p1-buf,stdout);p1=buf;}}
~Ostream_fwrite(){flush();}
}Ostream;
inline void print(int x){Ostream.print(x);}
inline void println(int x){Ostream.println(x);}
inline void print(char x){Ostream.out(x);}
inline void println(char x){Ostream.out(x);Ostream.out('\n');}
inline void print(ll x){Ostream.print(x);}
inline void println(ll x){Ostream.println(x);}
inline void print(double x,int y){Ostream.print(x,y);}
inline void println(double x,int y){Ostream.println(x,y);}
inline void print(char *s){Ostream.print(s);}
inline void println(char *s){Ostream.println(s);}
inline void println(){Ostream.out('\n');}
inline void flush(){Ostream.flush();}
//puts->write
char Out[OUT_SIZE],*o=Out;
inline void print1(int x){
static char buf[15];
char *p1=buf;if (!x)*p1++='0';if (x<0)*o++='-',x=-x;
while(x)*p1++=x%10+'0',x/=10;
while(p1--!=buf)*o++=*p1;
}
inline void println1(int x){print1(x);*o++='\n';}
inline void print1(ll x){
static char buf[25];
char *p1=buf;if (!x)*p1++='0';if (x<0)*o++='-',x=-x;
while(x)*p1++=x%10+'0',x/=10;
while(p1--!=buf)*o++=*p1;
}
inline void println1(ll x){print1(x);*o++='\n';}
inline void print1(char c){*o++=c;}
inline void println1(char c){*o++=c;*o++='\n';}
inline void print1(char *s){while (*s)*o++=*s++;}
inline void println1(char *s){print1(s);*o++='\n';}
inline void println1(){*o++='\n';}
inline void flush1(){if (o!=Out){if (*(o-1)=='\n')*--o=0;puts(Out);}}
struct puts_write{
~puts_write(){flush1();}
}_puts;
inline void print2(int x){printf("%d",x);}
inline void println2(int x){printf("%d\n",x);}
inline void print2(char x){printf("%c",x);}
inline void println2(char x){printf("%c\n",x);}
inline void print2(ll x){
#ifdef _WIN32
printf("%I64d",x);
#else
#ifdef __linux
printf("%lld",x);
#else
puts("error:can't recognize the system!");
#endif
#endif
}
inline void println2(ll x){print2(x);printf("\n");}
inline void println2(){printf("\n");}
#undef ll
#undef OUT_SIZE
#undef BUF_SIZE
};
using namespace fastIO;
LL gcd(LL a,LL b) {
while(b) {
LL c = a%b;
a = b;
b = c;
}
return a;
}
struct frac {
LL x,y;
frac() {frac(0,1);}
frac(LL xx,LL yy=1) {
//assert(yy);
if(yy != 1) {
LL d = gcd(xx,yy);
xx /= d; yy /= d;
}
if(yy<0) xx = -xx,yy = -yy;
x = xx; y = yy;
}
void print(){
printf("%lld/%lld\n",x,y);
}
};
frac operator +(frac a,frac b) {
return frac(a.x*b.y+b.x*a.y,a.y*b.y);
}
frac operator -(frac a,frac b) {
return frac(a.x*b.y-b.x*a.y,a.y*b.y);
}
frac operator *(frac a,frac b) {
return frac(a.x*b.x,a.y*b.y);
}
frac operator /(frac a,frac b) {
return frac(a.x*b.y,a.y*b.x);
}
bool operator <=(frac a,frac b) {
return a.x*b.y <= b.x*a.y;
}
bool operator ==(frac a,frac b) {
return a.x*b.y == b.x*a.y;
}
struct haha {
LL a,b;
}a[SZ];
bool cmp(haha a,haha b) {
return a.b*b.a < b.b*a.a;
}
mt19937 rd(time(0));
int randlr(int l,int r) {
return rd()%(r-l+1)+l;
}
void getdata() {
int T = 5;
printf("%d\n",T);
while(T --) {
int n = 1e5,C = randlr(1,1e9);
printf("%d %d\n",n,C);
for(int i = 1;i <= n;i ++) {
printf("%d %d\n",randlr(1,1000),randlr(-1000,1000));
}
}
}
frac ans[SZ];
int len;
int main() {
// freopen("04.in","w",stdout); getdata(); return 0;
//freopen("04.in","r",stdin); freopen("04.out","w",stdout);
int T;
read(T);
while(T --) {
int n;
read(n);
int CC; read(CC);
frac C = frac(CC,1);
for(int i = 1;i <= n;i ++) {
read(a[i].a),read(a[i].b);
a[i].b = -a[i].b;
}
sort(a+1,a+1+n,cmp);
frac now = frac(-INF,1),nowC = frac(0,1);
LL q = 0,h = 0;
for(int i = 1;i <= n;i ++) h = h + a[i].a;
// for(int i = 1;i <= n;i ++) printf("%lld %lld\n",a[i].a,a[i].b);
for(int i = 1;i <= n;i ++) {
nowC = nowC + a[i].a * (frac(a[i].b,a[i].a) - now);
}
len = 0;
bool flag = 0;
for(int i = 1;i <= n + 1;i ++) {
if(i <= n) {
if(q == h) {
if(nowC == C) {
flag = 1;
break;
}
else {
nowC = nowC + (frac(a[i].b,a[i].a) - now) * (q-h);
now = frac(a[i].b,a[i].a);
q = q + a[i].a;
h = h - a[i].a;
continue;
}
}
/* cout << i << endl;
now.print();
C.print(); nowC.print();
q.print(); h.print();*/
frac d = (C - nowC) / (q-h);
// d.print();
if(d.x > 0 && now+d <= frac(a[i].b,a[i].a)) {
ans[++ len] = now+d;
}
nowC = nowC + (frac(a[i].b,a[i].a) - now) * (q-h);
now = frac(a[i].b,a[i].a);
q = q + a[i].a;
h = h - a[i].a;
}
else {
frac d = (C - nowC) / (q-h);
if(d.x > 0) {
ans[++ len] = now+d;
}
}
}
if(flag) println("-1");
else {
if(len == 0) { println("0"); continue; }
print(len); print(" ");
for(int i = 0;i < len;i ++) {
//printf("%lld/%lld%c",ans[i+1].x,ans[i+1].y,i+1==len?'\n':' ');
print(ans[i+1].x);
print('/');
print(ans[i+1].y);
if(i+1 != len) print(' ');
else print('\n');
}
}
}
}
E
注意到 K 很小,所以只需要对后半部分暴力即可。
F
签到题,直接上 z-algorithm
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef pair<LL,int> pli;
const int SZ = 1e6 + 10;
const int INF = 1e9 + 10;
const int mod = 1e9 + 7;
const LD eps = 1e-8;
LL read() {
LL n = 0;
char a = getchar();
bool flag = 0;
while(a > '9' || a < '0') { if(a == '-') flag = 1; a = getchar(); }
while(a <= '9' && a >= '0') { n = n * 10 + a - '0',a = getchar(); }
if(flag) n = -n;
return n;
}
int z[SZ];
void get_z(char s[]) { //z[i]:后缀i与原串的lcp长度
int n = strlen(s + 1);
int l = 1,r = 0;
for(int i = 2;i <= n;i ++) {
if(i >= l + r) {
int h = 0;
while(i + h <= n && s[i + h] == s[1 + h]) h ++;
z[i] = h;
}
else {
int k = i - l + 1;
if(i + z[k] < l + r) z[i] = z[k];
else {
int h = l + r - i;
while(i + h <= n && s[i + h] == s[1 + h]) h ++;
z[i] = h;
}
}
if(i + z[i] > l + r) l = i,r = z[i];
}
}
char s[SZ];
int main() {
int T = read();
while(T --) {
scanf("%s",s + 1);
get_z(s);
int n = strlen(s + 1);
LL ans = n - 1;
// for(int i = 1;i <= n;i ++) printf("%d ",z[i]); puts("");
for(int i = 2;i <= n;i ++) {
ans += z[i];
if(i+z[i]-1 == n) ans --;
}
printf("%lld\n",ans);
}
}
G
题意:求第一项是 x ,第 n 项是 y ,相邻两项之差不超过 2 的排列个数。 \(n \le 10^5, x<y\)
key:推公式
可以当成有 n 个格子,初始在 x ,要不重复遍历所有格子最终回到 y ,每步只能左右跳一格或两格,问路径个数。
容易发现一定满足以下流程:
- 先遍历完小于 x 的
- 把 [x+1,y-1] 全部跳完
- 遍历完所有大于 y 的之后再回到 y。
我们发现第一步和第三步的方案数一定是 1 。所以只用考虑中间的情况。
当 x=1,y=n 时,容易写出递推式: \(f_n=f_{n-1}-f_{n-3}\)
如果 x=1, y!=n 或者 x!=1,y=n ,那么两边都限制了一步(例如前者的第三个流程,一定是先到 y-1 再到 y+1,不能从y-2直接跳到 y。所以方案数就是从 1 任意跳完前 y-1 个的方案数),方案数是 \(f_{y-x}\)
最后,如果当 x!=1 y!=n 时,中间一定是 x+1 跳到 y-1 ,方案数是 \(f_{y-x-1}\)。注意 y=x+1 时无解。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN=1e5+10;
const int mod=998244353;
int n,m,p1,p2,cnt=0;
LL f[MAXN];
int g[10];
int num[1111],use[1111];
int dfs(int d) {
if(d == n + 1) {
if(num[1] != p1 || num[n] != p2) return 0;
bool f = 0;
for(int i = 1;i < n;i ++) {
if(abs(num[i+1]-num[i]) > 2) f = 1;
}
if(!f) {
// for(int i = 1;i <= n;i ++) printf("%d ",num[i]); puts("");
}
return f^1;
}
int ans = 0;
for(int i = 1;i <= n;i ++) {
if(!use[i]) {
use[i] = 1;
num[d] = i;
ans += dfs(d+1);
use[i] = 0;
}
}
return ans;
}
int main(){
f[1]=f[0]=f[2]=f[3]=1;
for(int i=4;i<=100000;i++){
f[i]=f[i-1];
if (i>=3) f[i]+=f[i-3];
f[i]%=mod;
}
// for(int i = 0;i <= 10;i ++) printf("%lld ",f[i]); puts("");
int T; scanf("%d",&T);
while(T--){
scanf("%d%d%d",&n,&p1,&p2);
LL ans=0;
if(p2!=n&&p1!=1&&p2==p1+1) ans = 0;
else {
m=p2-p1;
if (p1==1 && p2!=n) {
ans=f[m];
}
if (p1!=1 && p2==n) {
ans=f[m];
}
if (p1==1 && p2==n){
ans=f[n];
}
if(p1!=1 && p2 != n) {
ans=f[m-1];
}
}
printf("%lld\n",ans);
}
}
H
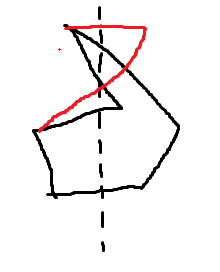
题意:给一个简单多边形,问是否移动一个点使其轴对称。注意它连出去的边还是之前相邻的两个点,并且对称轴两边的顶点数相同。 \(n \le 1000\)
key:计算几何
简单多边形的对称轴一定是某边的中垂线或者隔一个点的两点连线的中垂线,非常显然。
考虑枚举对称轴,然后check一下有多少个点没有找到对称点。如果大于 2 个显然无解,没有那么它本身就是轴对称,否则:
- 只有一个。那么这个点一定是最后一个点,并且是奇数个点。只需要把最后一个点放到对称轴上。
- 有两个。此时要注意不一定可行,因为有可能不simple
I
牛逼的求离散对数模板题,但是BSGS不能跑,需要Pohlig–Hellman这个牛逼算法
J
题意:有一个长度为 2*n 的未知排列,维护一个集合,初始集合包含前 n 个元素。每次会弹出一个最小的或者最大的,并把下一个元素加入。给出所有弹出的元素和最大还是最小,求构造一个字典序最小的合法2*n排列。 \(2*n \le 10^5\)
key:贪心
考虑处理出每个点可以放的数字集合,这么想可能很难,那么考虑处理处每个数字可以出现的位置,此时的限制就是数字之间的了。
首先对于一个已被弹出的元素,它一定在[1,i+n-1] 中出现。非弹出序列中的元素,一定在[1,2*n]中出现。
然而左端点不一定是 1 。如果对于 x ,如果第 i 次弹出的最小值比它大,那么它一定出现在 n+i 及之后。对于最大值同理。
这样我们就处理出一个比较紧的界,可以证明是充要的。
实际上这种题型之前做过( 点我搜索2018-2019 XIX Open Cup, Grand Prix of Korea 的 D 题),然而这次要求字典序最小。
对于可行解,可以直接从前往后,每次放当前可行集合中右端点最小的。原因是如果随便放,那么在未来可能出现多个元素同时到达了右端点,此时需要在前面找元素顶掉
然而我们发现,对于这个题,右端点除了 2*n ,其余的至多只有 1 个,并不会出现这种情况。所以只需要每次拿最小元素,如果有一个元素到达了它的右端点那么再放它即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
typedef pair<int,int> pii;
typedef pair<LL,int> pli;
const int SZ = 1e5 + 10;
const int INF = 1e9 + 10;
const int mod = 1e9 + 7;
const LD eps = 1e-8;
LL read() {
LL n = 0;
char a = getchar();
bool flag = 0;
while(a > '9' || a < '0') { if(a == '-') flag = 1; a = getchar(); }
while(a <= '9' && a >= '0') { n = n * 10 + a - '0',a = getchar(); }
if(flag) n = -n;
return n;
}
pii small[SZ],large[SZ];
int lb(pii a[],int l,int r,int val,bool f) {
r ++;
while(r-l>1) {
int mid = l + r >> 1;
if(f) {
if(a[mid].first < val) l = mid;
else r = mid;
}
else {
if(a[mid].first < val) r = mid;
else l = mid;
}
}
return a[l].second + 1;
}
int L[SZ],R[SZ],del[SZ],a[SZ],n;
vector<int> lst[SZ];
vector<int> ans;
bool work() {
ans.clear();
set<pii> sr;
set<int> sv;
for(int i = 1;i <= 2*n;i ++) {
for(int v : lst[i]) sv.insert(v),sr.insert(make_pair(R[v],v));
if(sv.empty()) return false;
while(del[sr.begin() -> second]) sr.erase(sr.begin());
int x;
if(sr.begin() -> first == i) {
x = sr.begin() -> second;
sr.erase(sr.begin());
sv.erase(x);
}
else {
int x = *sv.begin();
sv.erase(x);
}
del[x] = 1;
ans.push_back(x);
}
bool flag = 0;
set<int> s;
for(int i = 1;i <= n;i ++) s.insert(ans[i-1]);
for(int i = 1;i <= n;i ++) {
if(a[i]<0) {
int x = *s.begin(); s.erase(s.begin());
if(x != -a[i]) return false;
}
else {
int x = *prev(s.end()); s.erase(x);
if(x != a[i]) return false;
}
s.insert(ans[i+n-1]);
}
return true;
}
int main() {
//freopen("1.in","r",stdin); freopen("my.out","w",stdout);
int T = read();
while(T --) {
n = read();
int l1 = 0,l2 = 0;
small[++ l1] = make_pair(INF,0);
large[++ l2] = make_pair(0,0);
for(int i = 1;i <= 2*n;i ++) R[i] = 2*n,lst[i].clear(),del[i] = 0;
for(int i = 1;i <= n;i ++) {
int x = read(),v = abs(x);
a[i] = x;
R[v] = i+n-1;
if(x<0) {
while(l1 && small[l1].first < v) l1 --;
L[v] = small[l1].second + 1;
small[++ l1] = make_pair(v,i+n-1);
}
else {
while(l2 && large[l2].first > v) l2 --;
L[v] = large[l2].second + 1;
large[++ l2] = make_pair(v,i+n-1);
}
}
for(int i = 1;i <= 2*n;i ++) {
if(R[i] == 2*n) {
int r1 = lb(small,1,l1,i,0);
int r2 = lb(large,1,l2,i,1);
L[i] = max(r1,r2);
}
}
//for(int i = 1;i <= 2*n;i ++) printf("%d: %d %d\n",i,L[i],R[i]);
//cout << T << endl;
for(int i = 1;i <= 2*n;i ++) lst[L[i]].push_back(i);
if(!work()) { puts("-1"); continue; }
for(int i = 0;i < ans.size();i ++) {
printf("%d%c",ans[i],i+1==ans.size()?'\n':' ');
}
}
}



