78. 子集√

90. 子集 II

78题 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

作者：powcai

链接：https://leetcode-cn.com/problems/subsets/solution/hui-su-suan-fa-by-powcai-5/
来源：力扣（LeetCode）

回溯法：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        backtrack(0, nums, res, new ArrayList<Integer>());
        return res;

    }

    private void backtrack(int i, int[] nums, List<List<Integer>> res, ArrayList<Integer> tmp) {
        res.add(new ArrayList<>(tmp));!!!!!
        for (int j = i; j < nums.length; j++) {
            tmp.add(nums[j]);
            backtrack(j + 1, nums, res, tmp);
            tmp.remove(tmp.size() - 1);
        }
    }
}

此题可以用位掩码方法：

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/subsets/solution/hui-su-python-dai-ma-by-liweiwei1419/
来源：力扣（LeetCode）

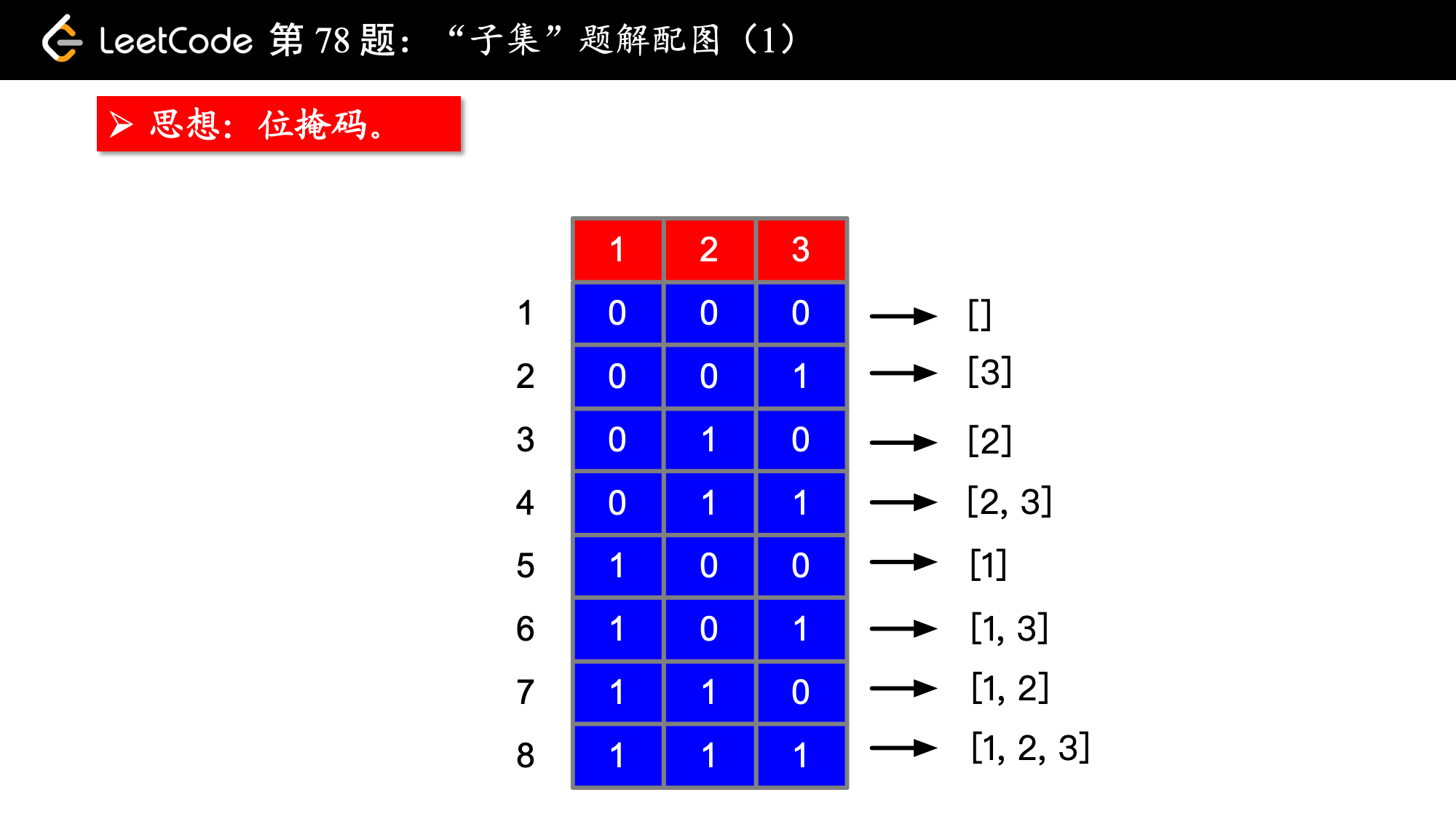
import java.util.ArrayList;
import java.util.List;

public class Solution5 {

    public List<List<Integer>> subsets(int[] nums) {
        int size = nums.length;
        int n = 1 << size;
        List<List<Integer>> res = new ArrayList<>();

        for (int i = 0; i < n; i++) {
            List<Integer> cur = new ArrayList<>();
            for (int j = 0; j < size; j++) {
                if (((i >> j) & 1) == 1) {
                    cur.add(nums[j]);
                }
            }
            res.add(cur);
        }
        return res;
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        Solution5 solution5 = new Solution5();
        List<List<Integer>> subsets = solution5.subsets(nums);
        System.out.println(subsets);
    }
}

39题数组总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。

说明：所有数字（包括 target）都是正整数。解集不能包含重复的组合。

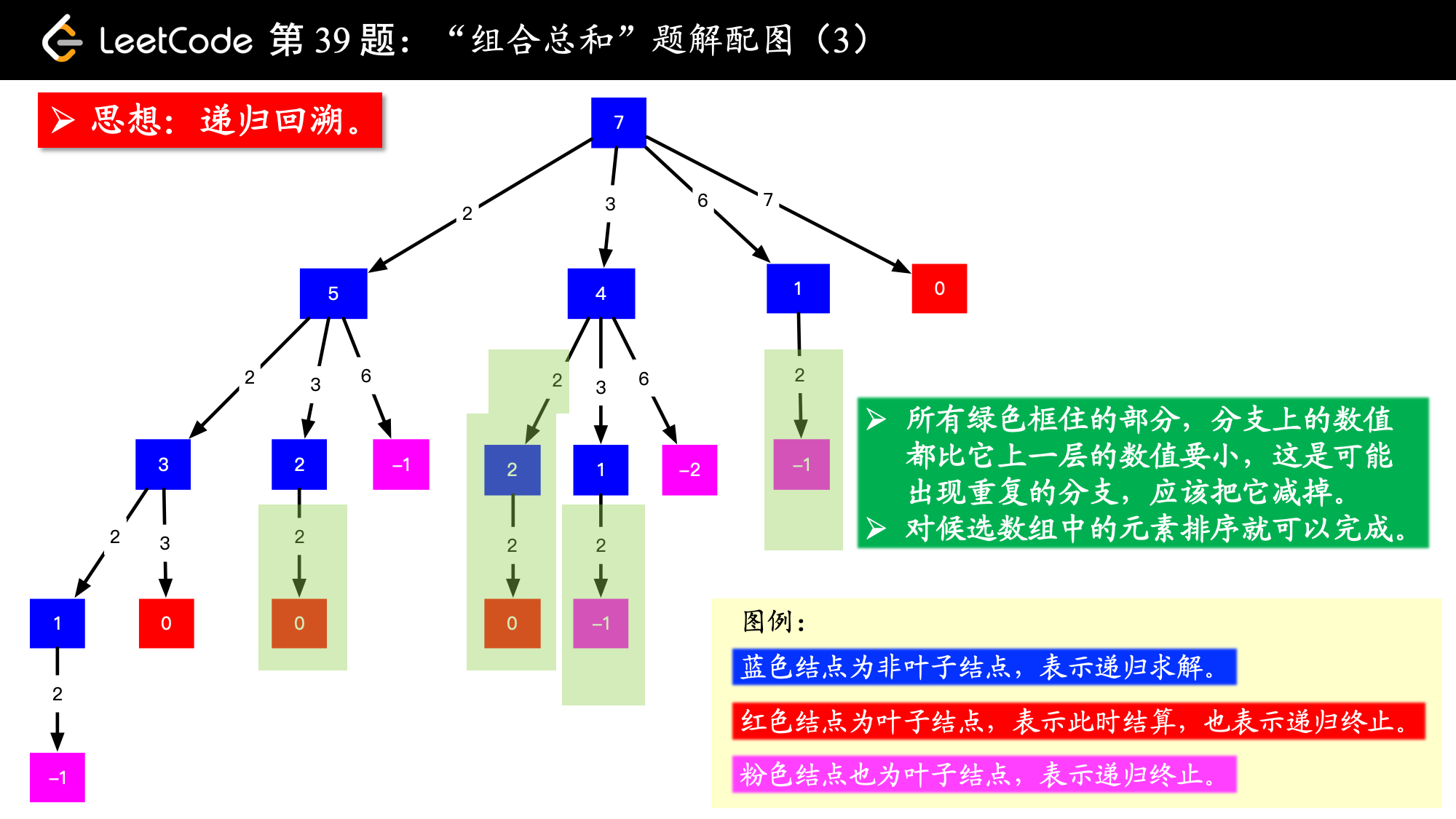
回溯法：

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/combination-sum/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-2/
来源：力扣（LeetCode）

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

public class Solution {

    private List<List<Integer>> res = new ArrayList<>();
    private int[] candidates;
    private int len;

    private void findCombinationSum(int residue, int start, Stack<Integer> pre) {
        if (residue == 0) {
            // Java 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来
            res.add(new ArrayList<>(pre));
            return;
        }
        // 优化添加的代码2：在循环的时候做判断，尽量避免系统栈的深度
        // residue - candidates[i] 表示下一轮的剩余，如果下一轮的剩余都小于 0 ，就没有必要进行后面的循环了
        // 这一点基于原始数组是排序数组的前提，因为如果计算后面的剩余，只会越来越小
        for (int i = start; i < len && residue - candidates[i] >= 0; i++) {
            pre.add(candidates[i]);
            // 【关键】因为元素可以重复使用，这里递归传递下去的是 i 而不是 i + 1
            findCombinationSum(residue - candidates[i], i, pre);
            pre.pop();
        }
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        if (len == 0) {
            return res;
        }
        // 优化添加的代码1：先对数组排序，可以提前终止判断
        Arrays.sort(candidates);
        this.len = len;
        this.candidates = candidates;
        findCombinationSum(target, 0, new Stack<>());
        return res;
    }

    public static void main(String[] args) {
        int[] candidates = {2, 3, 6, 7};
        int target = 7;
        Solution solution = new Solution();
        List<List<Integer>> combinationSum = solution.combinationSum(candidates, target);
        System.out.println(combinationSum);
    }
}

这里有一个更快的：

作者：powcai
链接：https://leetcode-cn.com/problems/combination-sum/solution/xue-yi-tao-zou-tian-xia-hui-su-suan-fa-by-powcai/
来源：力扣（LeetCode）

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates);
        //System.out.println(candidates);
        backtrack(candidates, target, res, 0, new ArrayList<Integer>());
        return res;
    }

    private void backtrack(int[] candidates, int target, List<List<Integer>> res, int i, ArrayList<Integer> tmp_list) {
        if (target < 0) return;
        if (target == 0) {
            res.add(new ArrayList<>(tmp_list));
            return;
        }
        for (int start = i; start < candidates.length; start++) {
            if (target < candidates[start]) break;
            //System.out.println(start);
            tmp_list.add(candidates[start]);
            //System.out.println(tmp_list);
            backtrack(candidates, target - candidates[start], res, start, tmp_list);
            tmp_list.remove(tmp_list.size() - 1);
        }
    }
}

40题组合总数||

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

作者：powcai
链接：https://leetcode-cn.com/problems/combination-sum-ii/solution/hui-su-xi-lie-by-powcai/
来源：力扣（LeetCode）

class Solution {
   public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        List<List<Integer>> res = new ArrayList<>();
        backtrack(res, candidates, target, 0, 0, new ArrayList<Integer>());
        return res;

    }

    private void backtrack(List<List<Integer>> res, int[] candidates, int target, int i, int tmp_sum, ArrayList<Integer> tmp_list) {
        if (tmp_sum == target) {
            res.add(new ArrayList<>(tmp_list));
            return;
        }
        for (int start = i; start < candidates.length; start++) {
            if (tmp_sum + candidates[start] > target) break;
            if (start > i && candidates[start] == candidates[start - 1]) continue;
            tmp_list.add(candidates[start]);
            backtrack(res, candidates, target, start + 1, tmp_sum + candidates[start], tmp_list);
            tmp_list.remove(tmp_list.size() - 1);
        }
    }
}

46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

作者：powcai
链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-by-powcai-2/
来源：力扣（LeetCode）

class Solution {
    public List<List<Integer>> permute(int[] nums) {

        List<List<Integer>> res = new ArrayList<>();
        int[] visited = new int[nums.length];
        backtrack(res, nums, new ArrayList<Integer>(), visited);
        return res;

    }

    private void backtrack(List<List<Integer>> res, int[] nums, ArrayList<Integer> tmp, int[] visited) {
        if (tmp.size() == nums.length) {
            res.add(new ArrayList<>(tmp));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (visited[i] == 1) continue;
            visited[i] = 1;
            tmp.add(nums[i]);
            backtrack(res, nums, tmp, visited);
            visited[i] = 0;
            tmp.remove(tmp.size() - 1);
        }
    }
}

更快方法：

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        if (nums == null || nums.length == 0) return res;
        List<Integer> list = new ArrayList<>();
        for (int num : nums) {
            list.add(num);
        }
        dfs(list, res, 0);

        return res;
    }

    private void dfs(List<Integer> nums, List<List<Integer>> res, int start) {
        if( start == nums.size()) {
            res.add(new ArrayList<>(nums));
        }
        else {
            for (int i = start; i < nums.size(); i++) {
                Collections.swap(nums, i, start);
                dfs(nums, res, start+1); //交换当前位置后，从下一个位置开始重新排列填充
                Collections.swap(nums, i, start); //重新排列后再恢复
            }
        }
    }
}

posted @ 2019-11-06 18:19 doyi 阅读(1224) 评论(0) 编辑收藏举报

刷新页面返回顶部

怕什么

大佬总结的leetcode回溯算法题目

公告