深度学习入门（一）——前馈网络和反向传播推导
本篇博文详细记录下我推导前馈网络和反向传播的过程。想要了解基本的神经网络构成，请参看Poll的笔记[Deep Learning] 神经网络基础。下面结合Charlotte77的https://www.cnblogs.com/charlotte77/p/5629865.html 中的例子来推导一遍。
1. 目标分析
如图1-1是一个简单的神经网络，仅有三层，每层仅有两个神经元。第一层是输入层，包含两个神经元、
，和截距项
；第二层是隐含层，包含两个神经元
、
和截距项
，第三层是输出
、
，每条线上标的是层与层之间连接的权重，激活函数我们默认为sigmoid函数。
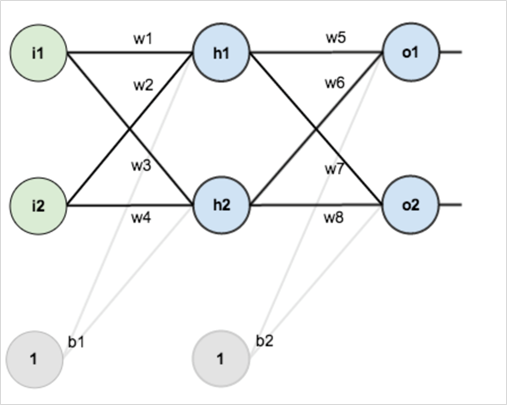
图 11 初始神经网络权重图
为他们赋上权重值，如图1-2所示：
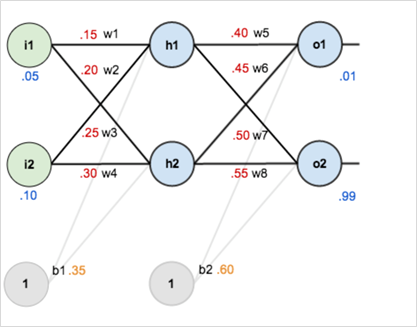
图 12 为神经网络赋初始值
目标：给出输入数据、
，使输出尽可能与原始输出
、
接近。
2. 前向传播
2.1 输入层à隐含层
隐藏神经元的加权和为：
隐藏神经元的加权和为：
隐藏神经元的输出为：
隐藏神经元的输出为：
2.2 隐含层à输出层
输出神经元的加权和为：
输出神经元的加权和为：
输出神经元的输出为：
输出神经元的输出为：
3. 反向传播
3.1 计算总误差
总误差为均方误差：
3.2 隐含层à输出层的权值更新
首先计算对整体误差产生了多少影响，需要对求偏导，同时由2.2可知，
只对
产生影响，又决定了
同理可以计算
将学习率设置为0.5，计算得到的更新值
同理可得：
3.3隐含层à输入层的权值更新
方法与上面的类似，但是要注意决定了
，而
决定了
，
对
和
均有影响，
和
分别决定了
和
，所以在求总误差对
偏导时，必须对
和
同时求偏导：
据此更新的值为
同理可得
从而得到、
和
的更新值：
如此所有的权重值便通过反向传播更新完毕，在这个例子中第一次迭代之后，总误差由0.29837110876下降至0.291027773694。迭代10000次后，总误差为0.000035085，输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。首次反向传播的代码见：https://github.com/DowTowne/Deep/blob/master/Introduce_to_deep_learning/01_back_propagation/back_propagation_cal.py，循环迭代的代码请参见：https://github.com/DowTowne/Deep/blob/master/Introduce_to_deep_learning/01_back_propagation/test_simple_neuralNetwork.py。
转载请注明出处。如有勘误，请多多指正！
参考 文献：
1. Poll的笔记：[Mechine Learning & Algorithm] 神经网络基础（http://www.cnblogs.com/maybe2030/p/5597716.html#3457159 ）
2. 一文弄懂神经网络中的反向传播法——BackPropagation（ https://www.cnblogs.com/charlotte77/p/5629865.html ）
