OWLQN算法
一、BFGS算法
算法思想如下:
Step1 取初始点,初始正定矩阵
,允许误差
,令
;
Step2 计算;
Step3 计算,使得
;
Step4 令;
Step5 如果,则取
为近似最优解;否则转下一步;
Step6 计算
,
,
令,转Step2.
优点:
1、不用直接计算Hessian矩阵;
2、通过迭代的方式用一个近似矩阵代替Hessian矩阵的逆矩阵。
缺点:
1、矩阵存储量为,因此维度很大时内存不可接受;
2、矩阵非稀疏会导致训练速度慢。
二、L-BFGS算法
针对BFGS的缺点,主要在于如何合理的估计出一个Hessian矩阵的逆矩阵,L-BFGS的基本思想是只保存最近的m次迭代信息,从而大大降低数据存储空间。对照BFGS,我重新整理一下用到的公式:
于是估计的Hessian矩阵逆矩阵如下:
把
带入上式,得:
假设当前迭代为k,只保存最近的m次迭代信息,(即:从k-m~k-1),依次带入,得到:
公式1:
算法第二步表明了上面推导的最终目的:找到第k次迭代的可行方向,满足:
为了求可行方向p,有下面的:
two-loop recursion算法
该算法的正确性推导:
1、令: ,递归带入q:
相应的:
2、令:
于是:
这个two-loop recursion算法的结果和公式1*初始梯度的形式完全一样,这么做的好处是:
1、只需要存储、
(i=1~m);
2、计算可行方向的时间复杂度从O(n*n)降低到了O(n*m),当m远小于n时为线性复杂度。
总结L-BFGS算法的步骤如下:
Step1: 选初始点,允许误差
,存储最近迭代次数m(一般取6);
Step2: ;
Step3: 如果 则返回最优解
,否则转Step4;
Step4: 计算本次迭代的可行方向:;
Step5: 计算步长,对下面式子进行一维搜索:
;
Step6: 更新权重x:
;
Step7: if k > m
只保留最近m次的向量对,需要删除();
Step8: 计算并保存:
;
Step9: 用two-loop recursion算法求得:
;
k=k+1,转Step3。
需要注意的地方,每次迭代都需要一个,实践当中被证明比较有效的取法为:
三、OWL-QN算法
1、问题描述
对于类似于Logistic Regression这样的Log-Linear模型,一般可以归结为最小化下面这个问题:
其中,第一项为loss function,用来衡量当训练出现偏差时的损失,可以是任意可微凸函数(如果是非凸函数该算法只保证找到局部最优解),后者为regularization term,用来对模型空间进行限制,从而得到一个更“简单”的模型。
根据对模型参数所服从的概率分布的假设的不同,regularization term一般有:L1-norm(模型参数服从Gaussian分布);L2-norm(模型参数服从Laplace分布);以及其他分布或组合形式。
L2-norm的形式类似于:
L1-norm的形式类似于:
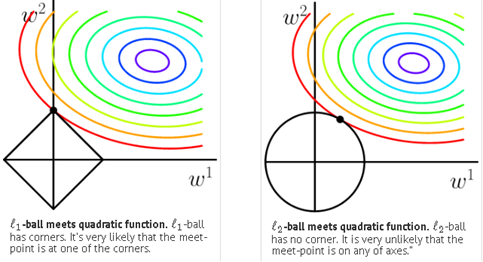
L1-norm和L2-norm之间的一个最大区别在于前者可以产生稀疏解,这使它同时具有了特征选择的能力,此外,稀疏的特征权重更具有解释意义。
对于损失函数的选取就不在赘述,看两幅图:
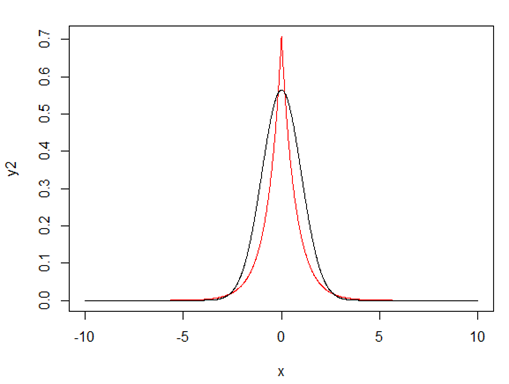
图1 - 红色为Laplace Prior,黑色为Gaussian Prior
图2 直观解释稀疏性的产生
对LR模型来说损失函数选取凸函数,那么L2-norm的形式也是的凸函数,根据最优化理论,最优解满足KKT条件,即有:,但是L1-norm的regularization term显然不可微,怎么办呢?
2、Orthant-Wise Limited-memory Quasi-Newton
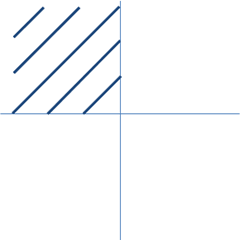
OWL-QN主要是针对L1-norm不可微提出的,它是基于这样一个事实:任意给定一个维度象限,L1-norm 都是可微的,因为此时它是一个线性函数:
图3 任意给定一个象限后的L1-norm
OWL-QN中使用了次梯度决定搜索方向,凸函数不一定是光滑而处处可导的,但是它又符合类似梯度下降的性质,在多元函数中把这种梯度叫做次梯度,见维基百科http://en.wikipedia.org/wiki/Subderivative
举个例子:

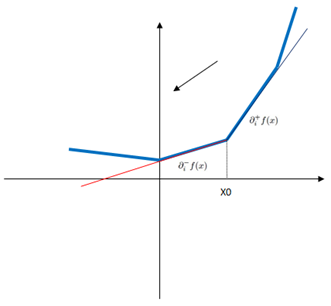
图4 次导数
对于定义域中的任何x0,我们总可以作出一条直线,它通过点(x0, f(x0)),并且要么接触f的图像,要么在它的下方。这条直线的斜率称为函数的次导数,推广到多元函数就叫做次梯度。
次导数及次微分:
凸函数f:I→R在点x0的次导数,是实数c使得:
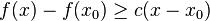
对于所有I内的x。可以证明,在点x0的次导数的集合是一个非空闭区间[a, b],其中a和b是单侧极限
它们一定存在,且满足a ≤ b。所有次导数的集合[a, b]称为函数f在x0的次微分。
OWL-QN和传统L-BFGS的不同之处在于:
1)、利用次梯度的概念推广了梯度
定义了一个符合上述原则的虚梯度,求一维搜索的可行方向时用虚梯度来代替L-BFGS中的梯度:
怎么理解这个虚梯度呢?见下图:
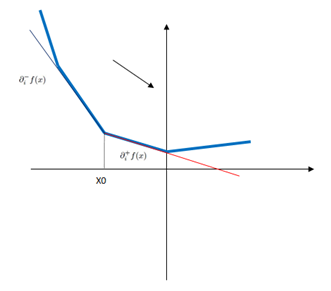
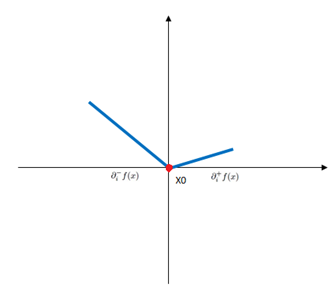
对于非光滑凸函数,那么有这么几种情况:
图5
图6
图7 otherwise
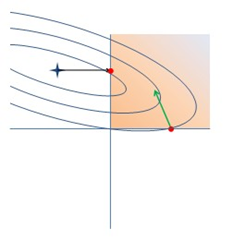
2)、一维搜索要求不跨越象限
要求更新前权重与更新后权重同方向:
图8 OWL-QN的一次迭代
总结OWL-QN的一次迭代过程:
–Find vector of steepest descent
–Choose sectant
–Find L-BFGS quadratic approximation
–Jump to minimum
–Project back onto sectant
–Update Hessian approximation using gradient of loss alone
最后OWL-QN算法框架如下:
与L-BFGS相比,第一步用虚梯度代替梯度,第二、三步要求一维搜索不跨象限,也就是迭代前的点与迭代后的点处于同一象限,第四步要求估计Hessian矩阵时依然使用loss function的梯度(因为L1-norm的存在与否不影响Hessian矩阵的估计)。
四、参考资料
1、Galen Andrew and Jianfeng Gao. 2007. 《Scalable training of L1-regularized log-linear models》. In Proceedings of ICML, pages 33–40.
3、http://research.microsoft.com/en-us/downloads/b1eb1016-1738-4bd5-83a9-370c9d498a03/default.aspx

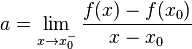
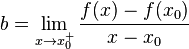
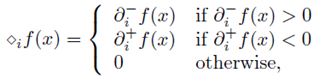
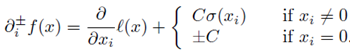
![8]O)3Y(ZOLX5C1AI9YXP72M 8]O)3Y(ZOLX5C1AI9YXP72M](http://images.cnblogs.com/cnblogs_com/vivounicorn/201206/201206251308208914.jpg)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号